1. DSGN313
GROUP F1
Design of a Formula Student Suspension System
Alex Mott
Ryan Bruton
Ryan Summers
Paul Pointon
Peter Valentine
Jonny Haughton
James Hyder
23/04/2015
Plymouth University

2. Group F1 1
Abstract
This project explains the development of a suspension system for an FSAE student
car. The chosen design was a push-rod double wishbone suspension system and
followed the design process from concept through to detail design. The concept
design was a standard double wishbone suspension system but aerodynamic
limitations deemed that this was not the optimum design. Calculations and CAD set
the foundations for the design process which led to difficulties in material selection.
To complete an in depth analysis, SolidWorks FEA was used for structural analysis
and MatLab for system response. The design went through several iterations to
optimise the final model. A final cost analysis was carried out to provide evidence for
viability for the ongoing project. The project was successful in developing a fully
functional suspension system that would meet FSAE criteria, along with design
specification that was initially set.
Acknowledgements
The group would like to thank Adam Kyte for his consistent support throughout the
project and his aid in helping of the overcoming of certain barriers. The group would
also like to thank Matthew Sharman for providing elaborate information about the
Auburn groups work. The group would also like to thank Plymouth University for the
access to any equipment/technology that was used throughout the design process.

3. Group F1 2
Contents
Abstract ..............................................................................................................1
Acknowledgements ..............................................................................................1
List of Figure .......................................................................................................4
List of Tables.......................................................................................................5
Nomenclature ......................................................................................................6
1. Introduction.....................................................................................................7
1.1 Aims & Objectives .......................................................................................7
2. The Concept ....................................................................................................7
3. The Final Design ..............................................................................................8
4. The Design Process..........................................................................................8
4.1. FMECA Analysis..........................................................................................9
4.2. Calculations ............................................................................................. 10
4.2.1. Forces............................................................................................... 10
4.2.2. Ackerman.......................................................................................... 11
4.2.3. Spring Rate Selection......................................................................... 12
4.2.4. Track Width....................................................................................... 12
4.2.5. Suspension Geometry ........................................................................ 13
4.2.6. Roll Centre and Instant Centre ........................................................... 17
4.2.7. Stresses ............................................................................................ 18
4.2.8. System Response............................................................................... 19
4.3. Material selection ..................................................................................... 20
4.4. Re-Iteration, Alterations & Design Development......................................... 23
4.4.1. Rocker .............................................................................................. 23
4.4.2. Push-rod ........................................................................................... 24
4.4.3. Wheel Hub ........................................................................................ 24
4.4.4. Anti-Roll Bar ...................................................................................... 24
4.4.5. Brake Calliper .................................................................................... 25
4.5. Manufacturing Methods ............................................................................ 25
4.5.1. Hub .................................................................................................. 25
4.5.2. Adjustable Rods................................................................................. 26

4. Group F1 3
4.5.3. Wishbones ........................................................................................ 26
4.5.4. Rocker .............................................................................................. 27
4.5.5. Bushings ........................................................................................... 27
4.6. Imported Parts......................................................................................... 27
4.6.1. Dampers ........................................................................................... 28
4.6.2. Springs ............................................................................................. 28
4.6.3. Rod End ............................................................................................ 28
4.6.4. Nuts, Bolts & Fixings .......................................................................... 28
4.6.5. Washers............................................................................................ 29
4.7. Detail Design ........................................................................................... 29
4.7.1. Lower Wishbone ................................................................................ 30
4.7.2. Upper Wishbone ................................................................................ 30
4.7.3. Push-rod ........................................................................................... 30
4.7.4. Positioning arm & Anti-roll bar ............................................................ 31
4.7.5. Rocker .............................................................................................. 31
4.7.6. Hub .................................................................................................. 32
4.7.7. Springs and Dampers......................................................................... 32
4.7.8. Full assembly..................................................................................... 32
4.7.9. Tolerances ........................................................................................ 32
4.7.10. Altering Geometry............................................................................ 33
4.8. Simulation Analysis................................................................................... 33
4.8.1. FEA................................................................................................... 33
4.8.2. MatLab.............................................................................................. 37
4.9. Environmental Impact .............................................................................. 43
4.10. Cost Analysis.......................................................................................... 44
5. Conclusion..................................................................................................... 45
6. Recommendations & Advisories....................................................................... 46
7. References .................................................................................................... 47

5. Group F1 4
List of Figure
Figure 1: Front concept suspension design
Figure 2: Rear final suspension design
Figure 3: Pull-rod vs push-rod (Formula1-dictionary (2015)
Figure 4: FMECA analysis screenshot
Figure 5: Ackerman theory (Popa, 2005)
Figure 6: Graph showing required steering lock
Figure 7: Motion ratio and mounting angle
Figure 8: Graph showing effects of track width on cornering speed
Figure 9: Showing different suspension geometries
Figure 10: Existing concept wishbone design
Figure 11: Final wishbone design
Figure 12: Toe change for concept design
Figure 13: Toe change through compression of final design
Figure 14: Steering system showing interaction with steering arm
Figure 15: Proposed steering arm position
Figure 16: Positive vs negative camber (Blueriverfleet, 2015)
Figure 17: Camber angle for maximum tyre contact
Figure 18: Camber through compression with optimised static angle
Figure 19: Roll and instant centre locations (Theander, 2004)
Figure 20: Concept wishbone arrangement
Figure 21: Final wishbone arrangement
Figure 22: Graph showing first order suspension system response settling time
Figure 23: Level 2 CES EduPack search, metals with yield strength over 100MPa
Figure 24: Yield strength comparison for HSLAYS550(Red) and AISI4140(Yellow)
Figure 25: Spring and damper reposition
Figure 26: Rocker geometry change
Figure 27: Push-rod geometry change
Figure 28: Wheel hub geometry change
Figure 29: Anti-roll bar geometry change
Figure 30: Change in brake calliper
Figure 31: Rear wheel hub
Figure 32: Estimate for the wheel hub manufacture from custompart.net
Figure 33: Rear lower wishbone
Figure 34: Rocker
Figure 35: Bushing
Figure 36: Damper selection comparison
Figure 37: Imported springs
Figure 38: Imported rod end
Figure 39: 70mm M12 partial threaded bolt

6. Group F1 5
Figure 40: M12 nylock nut
Figure 41: Bushing locations
Figure 42: Bushing and rod end assembly
Figure 43: Exploded view of rear lower wishbone
Figure 44: Exploded view of rear upper wishbone
Figure 45: Push-rod assembly
Figure 46: Example of flats on components
Figure 47: Positioning arm assembly
Figure 48: Flats locations
Figure 49: Rocker assembly
Figure 50: Rear hub with bushings
Figure 51: Rebound adjustment
Figure 52: Rear left assembly
Figure 53: Rear lower wishbone FEA analysis
Figure 54: Rear upper wishbone FEA analysis
Figure 55: Rear push-rod FEA analysis
Figure 56: Rocker plate
Figure 57: Rocker FEA analysis
Figure 58: Rear wheel hub FEA analysis
Figure 59: Second order model of the suspension system
Figure 60: Block diagram representing equations 35 & 36, respectively
Figure 61: Block diagram representing equations 37 & 38, respectively
Figure 62: Block diagram representing K1 in terms of displacement
Figure 63: Block diagram including damping force of damper 1
Figure 64: Block diagram including the force from spring 2
Figure 65: Block diagram including the force from damper 2
Figure 66: The final model used to analyse system response to a 0.01m bump
Figure 67: Displacement response for the front wheel hitting 0.01m bump
Figure 68: Acceleration response for the front wheel hitting 0.01m bump
Figure 69: Displacement response for the rear wheel hitting 0.01m bump
Figure 70: Acceleration response for the rear wheel hitting 0.01m bump
List of Tables
Table 1: Mass comparison of aluminium and steel components
Table 2: CES EduPack search of typical automotive suspension materials
Table 3: Geometry Alteration
Table 4: Multiple buckling cases for upper wishbone
Table 5: MatLab input parameters
Table 6: MatLab output properties
Table 7: CO2 and energy analysis of steel components
Table 8: Cost analysis

7. Group F1 6
Nomenclature
Symbol Definition Units Symbol Definition Units
m Mass kg v Velocity m/s
CG Centre of Gravity m t Travel mm
W Width m WR Wheel Rate N/mm
L Length m MR Motion Ratio
y Height m ACF Angle Correction Factor
F Force N SR Spring Rate
r Radius m SF Suspension Frequency Hz
Ng g's pulled through
cornering
- ζ Damping Ratio -
CSA Cross Sectional Area m2
k Radius of Gyration
I Second Moment of Area m4
S Slenderness Ratio
σ Stress Pa c Crushing Strength
Cb Buckling Load N Cc Crushing Load Pa
RL Rankine Load N y Distance from Centroid M
T Torque Nm
Term Definition
Bump Steer Non consistent toe angle causes wheels to turn during compression,
without driver input
Feather(ing) Increased wear on the inner or outer edge of the tyre
RWD Rear wheel drive
Wheel Rate (WR) Amount of force required to displace a wheel 1mm upward from
ground
Jounce Spring travel in compression
Rebound Spring travel in extension
FEA Finite Element Analysis
FMECA Failure modes effect criticality analysis
AG Auburn Group
HSLA High strength low alloy

8. Group F1 7
1. Introduction
This report outlines the design process carried out by a group of 7, final year BEng
(Hons) Mechanical Engineering students at Plymouth University, in order to build
upon a proposed concept designed by the 2013/2014 Auburn group (AG). The
design will be developed into a fully functional suspension system, to incorporate
into a race car that can compete at a Formula Society of Automotive Engineers
(FSAE) event.
The purpose is to have the proposed suspension system implemented into the
existing concept car, with the ultimate goal of Plymouth University competing in the
FSAE annual meetings, although this will require additional work to optimise the
existing concept.
The suspension system aims to keep the car on the road with maximum traction to
the tyres. It should help absorb energy from going over bumps, reduce the amount
of roll on a car when going round a corner, as well as maintain a safe environment
enabling the driver to drive the car to its full potential.
1.1 Aims & Objectives
The main aim was to fully develop the suspension system from the concept design
presented by the AG.
 Carry out all necessary theoretical tasks thoroughly to develop and optimise a
suspension system
 Evolve a theoretical design into a CAD model and enable manufacturing by
evaluating and choosing appropriate materials, manufacturing methods and
imported parts
 Work effectively as a team and develop and understanding of the work
involved and the importance in engineering of going in-depth into a detail
design for a product
 Use effective project management tools in order to keep on track and gain
experience working in an engineering team
2. The Concept
The group was presented with a conceptual design for
a double wishbone suspension system to be
implemented on a formula student car. The concept
needed to be further developed, intricately designing
components, using theoretical and computational
methods, to ensure confidence that the final design will
work under the conditions that it will be exposed to.
Figure 1: Front concept
suspension design

9. Group F1 8
3. The Final Design
The final design is a push-rod double wishbone suspension system. The group
decided to deviate away from the concept standard double wishbone suspension due
to its aerodynamic limitations. This was done so the final suspension system could
go straight to manufacture when the University has a completed formula student car
design. Therefore, avoiding further work on the suspension system. The final design
can be seen in Figure 2.
4. The Design Process
The drawback of the concept double wishbone suspension system, see Figure 1, is
that it causes aerodynamic drawbacks, as all of the components are kept outside of
the car. For the group to develop a system that would not have to be redesigned in
the future, it was decided that the concept would need to be improved upon. To do
this there was a choice of two advancements that could be taken.
 Push-rod suspension system
 Pull-rod suspension system
Both methods have been used in Formula 1, to bring the components inside the
chassis. However, the push-rod is currently favoured. The pull-rod suspension
system brings all the parts lower to the ground. Thus, lowering centre of gravity and
inducing a bending moment on the pull-rod, see Figure 3. Due to the induced
bending moment on the pull-rod, as well as it not being as commonly adopted in
other cars, it was decided the push-rod suspension system would be used.
Upper Wishbone
Rocker
Anti-Roll Bar
Lower Wishbone
Toe Adjustment Bar
Pushrod
Shocks
Wheel Hub
Figure 2: Rear final suspension design

10. Group F1 9
The initial concept did not contain an anti-roll bar, which would have to be
implemented into the new design to increase performance characteristics, by helping
the tyres maintain as much contact with the road as possible.
4.1. FMECA Analysis
A FMECA analysis was used to determine where faults, flaws and failures could
potentially occur. Therefore, anything that could cause a problem within the design
could be filtered out before any major work went into it.
Many failure modes were considered, examples of these were as follows:
 Over/understeer
o A negligible severity as it would result in performance reduction, which
is not as important as a person’s safety. Expected as a frequent
occurring failure mode, potential as a common problem within a race.
 Excessive vibration
o An undesirable failure as it would deteriorate driver comfort. Possibility
of loosening components. A failure that is unlikely to occur as
avoidance would be simple.
 Heavy steering
o A negligible severity as only performance would be affected. Likely to
be a frequent risk as many simple aspects can cause it such as
underinflated tyres.
Figure 3: Pull-rod vs push-rod (Formula1-dictionary, 2015)
Push-rod Pull-rod
Figure 4: FMECA analysis screenshot

11. Group F1 10
 Failure of components
o A critical failure that could cause injury, event disqualification, or
damage to the University’s reputation. Considered unlikely due to
thorough analysis, as well as sufficient testing before event occurs.
The full FMECA, containing all potential failure modes, can be viewed in the
calculations spreadsheet, FMECA worksheet. A number of mitigating actions were
taken such as sufficient calculations/testing, and ensuring reputable suppliers for
parts, to reduce possible failure modes. As the severity of the failure modes will
remain, the frequency at which they may occur was addressed.
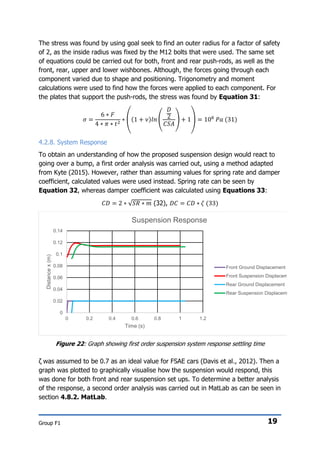
4.2. Calculations
4.2.1. Forces
The first place to start was to calculate the centre of gravity of the car in order to
determine the weight transfer under dynamic conditions. This was done by
gathering x, y and z coordinates, and the mass values for the main components.
Equation 1 was used to find the centre of gravity in the y direction:
𝐶𝐺 𝑦 =
𝑚 𝑐ℎ𝑎𝑠𝑠𝑖𝑠 ∗ 𝑦𝑐ℎ𝑎𝑠𝑠𝑖𝑠 + 𝑚 𝑒𝑛𝑔𝑖𝑛𝑒 ∗ 𝑦 𝑒𝑛𝑔𝑖𝑛𝑒 + 𝑚 𝑑𝑟𝑖𝑣𝑒𝑟 ∗ 𝑦 𝑑𝑟𝑖𝑣𝑒𝑟 + 𝑚 𝑓𝑢𝑒𝑙 𝑡𝑎𝑛𝑘 ∗ 𝑦𝑓𝑢𝑒𝑙 𝑡𝑎𝑛𝑘
𝑚 𝑐ℎ𝑎𝑠𝑠𝑖𝑠 + 𝑚 𝑒𝑛𝑔𝑖𝑛𝑒 + 𝑚 𝑑𝑟𝑖𝑣𝑒𝑟 + 𝑚 𝑓𝑢𝑒𝑙 𝑡𝑎𝑛𝑘
. . (1)
The process was repeated for the z coordinates of each component. It was assumed
that the x coordinate centre of gravity would lie at the car centreline. The minimum
track width to compete in the static 60ͦ test was calculated using Equation 2:
𝑊𝑡𝑟𝑎𝑐𝑘 𝑚𝑖𝑛 = (2 ∗ 𝐶𝐺 𝑦 ∗ tan(60)) − 𝑊𝑡𝑦𝑟𝑒 = 2 ∗ 0.325 ∗ tan(60) − 0.25 = 0.876 (2)
Using the centre of gravity, the dynamic forces were calculated, starting with the
linear forces. Using performance data for the AG proposed Honda CBR 600 engine,
and a mass conversion, an acceleration rate of 1.96 m/s2 was obtained. The vertical
forces acting on the front and rear axles were then calculated using Equations 3
and 4:
𝐹𝑓 =
𝐶𝐺𝑟
𝐿
∗ 𝑚 ∗ 𝑔 −
𝐶𝐺 𝑦
𝐿
𝑚 ∗ 𝑎 = 1083 𝑁 (3)
𝐹𝑟 =
𝐶𝐺𝑟
𝐿
∗ 𝑚 ∗ 𝑔 +
𝐶𝐺 𝑦
𝐿
𝑚 ∗ 𝑎 = 2616 𝑁 (4)
The maximum deceleration rate was calculated, assuming that braking causes a
complete weight transfer to the front wheels, to the point the wheels start skidding.
𝑎−1
=
𝜇 ∗ 𝑊
𝑚 𝑐
=
0.7 ∗ 3698.7[𝑁]
377[𝑘𝑔]
= 6.9 [
𝑚
𝑠2
] (5)
The 6.9m/s2 deceleration rate equates to 0.7g. However, this value is widely taken
to be 1.5g to act as a factor of safety. The vertical forces obtained were: 2268.7 N

12. Group F1 11
on the front, and 1429.7 N on the rear.
Using the tightest corner of 4.5m radius, the lateral forces at each wheel were
calculated for a left hand turn, using Equations 6-8:
𝐹𝑐 =
𝑚 ∗ 𝑣2
𝑟
= 8377.8 𝑁 (6)
𝐹𝑓𝑟 = 0.5 ∗ (𝑚 ∗ 𝑔 + (𝐹𝑐 ∗
𝐶𝐺 𝑦
0.5 ∗ 𝐿
)) ∗ 𝐶𝐺𝑟 = 1951 𝑁 (7)
𝐹𝑟𝑟 = 0.5 ∗ (𝑚 ∗ 𝑔 + (𝐹𝑐 ∗
𝐶𝐺 𝑦
0.5 ∗ 𝐿
)) ∗ 𝐶𝐺𝑧 = 3953 𝑁 (8)
(Bansal, 2005)
4.2.2. Ackerman
Ackerman steering theory was used to ensure the wheel
lock could accommodate the sharpest turn; it was
important to determine turning calculations that would
give a specified wheel lock, dependant on the wheel
base.
Using the AG geometry, the turning dimensions could be
calculated for the wheel base of the final design. Using
Equation 9 the wheel lock was calculated:
𝜃𝑜 = 𝑡𝑎𝑛−1
(
1
1
tan(𝜃𝑖)
+
𝑊𝑡𝑟𝑎𝑐𝑘
𝑊𝑙𝑒𝑛𝑔𝑡ℎ
) = 22° (9)
Equations 10-11 were used to calculate
the radial distance to the rear and to the
centre of gravity could be calculated:
𝐿 𝑟 =
𝑊 𝑙𝑒𝑛𝑔𝑡ℎ
tan(𝜃 𝑖)
+
𝑊 𝑡𝑟𝑎𝑐𝑘
2
= 3.68 𝑚 (10)
𝐿 𝐶𝐺 = √𝐿 𝑟
2 + 𝐶𝐺𝑟
2 = 3.73 𝑚 (11)
Utilising a parametric spreadsheet,
different track and wheelbase lengths
could be used to calculate the outer angle
necessary.
20
30
40
1 1.5 2 2.5
Insidewheellock[°]
Wheelbase [m]
Wheel Lock Requirement
Figure 6: Graph showing required
steering lock
Figure 5: Ackerman theory
(Popa, 2005)

13. Group F1 12
4.2.3. Spring Rate Selection
FSAE rules state the maximum wheel travel must be limited to 25.4mm jounce and
rebound. The maximum load at any one wheel is less than double the force due to
the cars self-weight. Thus, the spring rates (SR) have been selected to sit the car at
25.4mm compression under static load. The wheel rate (WR) was determined using
half the static load on one axle.
𝑊𝑅 =
0.5 ∗ 𝑊𝑟
𝑡 𝑚𝑎𝑥
=
0.5 ∗ 2476[𝑁]
25.4[𝑚𝑚]
= 48.7 [
𝑁
𝑚𝑚
] (12)
The motion ratio (MR) is the ratio of shock, or in this designs case, push-rod
mounting position (D1) to the lower wishbone hub mounting (D2). The angle
correction factor (ACF) relates the shock mounting angle to the vertical, as labelled
in Figure 7.
𝑀𝑅 =
𝐷1
𝐷2
=
267.3[𝑚𝑚]
346.1[𝑚𝑚]
= 0.77 (13)
𝐴𝐶𝐹 = cos(𝐴) = cos(35.4˚) = 0.815 (14)
𝑆𝑅 =
𝑊𝑅
𝑀𝑅2 ∗ 𝐴𝐶𝐹
=
48.7 [
𝑁
𝑚𝑚
]
0.772 ∗ 0.815
= 100.8 [
𝑁
𝑚𝑚
] (15)
The procedure carried out for the front suspension gave a spring rate of 48.9N/mm.
Combining jounce and rebound, the total spring travel distance is 50.8mm,
Equation 16 was used to determine how much travel is used by the front and rear
suspension under dynamic loadings. W reflects the vertical force at the rear right
hand wheel going around a left hand corner, at full acceleration. This load case is
the maximum that could occur at a rear wheel and still within the design limits.
𝑡 𝑢𝑠𝑒𝑑 =
𝑊
𝑆𝑅 ∗ 𝑀𝑅2 ∗ 𝐴𝐶𝐹
=
2454.6[𝑁]
100.8 [
𝑁
𝑚𝑚
] ∗ 0.772 ∗ 0.815
= 50.3[𝑚𝑚](16)
4.2.4. Track Width
Equation 17 determines the maximum speed that the car could go around a corner,
based on the first instant the inside wheels exert zero force on the track.
𝑣 𝑚𝑎𝑥 = √
𝑟 ∗ 𝑁𝑔 ∗ 𝑔 ∗ 𝑊𝑡𝑟𝑎𝑐𝑘
2 ∗ 𝐶𝐺 𝑦
(17)
Figure 7: Motion ratio and mounting angle

14. Group F1 13
Figure 9: Showing different suspension
geometries
Ng is an assumed value of 1.7g, which is the amount of g’s the car can withstand
through cornering. This was based on FSAE stating the static 60° tilt roughly
replicated 1.7g cornering (SAE rules, 2014).
4.2.5. Suspension Geometry
Theander (2004) gives guidelines for suspension geometries in accordance with
suspension theory and previous FSAE car data as listed below, and was considered
when designing the suspension geometry. The numbers correlate to Figure 9.
 Kingpin inclination: 0˚ to 8˚ (1)
 Scrub radius: 0mm to 10mm (2)
 Caster angle: 3˚ to 7˚ (5)
 Static camber: 0˚ to -4˚ (3)
 Roll centre height: 0mm to 50mm
 Toe: Minimise bump steer as much as
possible (4)
The spreadsheet used integrated trigonometry,
Pythagoras’ theorem and the current fixing points
at the hub and chassis to determine the wishbone
and pushrod dimensions as well as scrub radius,
kingpin inclination, track width change, toe angle,
and camber angle throughout compression.
The existing concept used wishbones with mountings either side of the hub with no
adjustment for camber or toe, as shown in Figure 10. The proposed design shown
Figure 8: Graph showing effects of track width on cornering speed
0
5
10
15
20
25
30
0 5 10 15 20 25
MaximumCorneringspeed[m/s]
Cornering Radius [m]
1.4m
1.1m
1.2m
1.3m

15. Group F1 14
in Figure 11 has opted for a single mounting point to minimise weight, adjustment
inaccuracy and time. As a result an independent rear toe arm has been added into
the proposed design and the new mounting points fed into the spreadsheet.
Figure 10: Existing concept wishbone
design
Figure 11: Final wishbone design
4.2.5.1. Toe angle
For maximum grip and to prevent tyre feathering the toe angle should be zero.
However, for a RWD car during acceleration the wheels toe out slightly as the torque
loads cause deflection in the bushings. A 0.5⁰ degree toe in angle has been used on
the rear to counteract this. The same angle was set at the front, as the wheels are
being pushed by the RWD motor.
The initial toe arm, mounted perpendicular to the hub prevented positive wheel
displacement, shown in Figure 12. Iterating for different mounting positions, it was
found fixing the toe arm in line with the rear wishbone chassis mounting and offset
on the hub as in Figure 11, allowed full suspension travel whilst offering the
minimum change in toe angle, shown in Figure 13.
Figure 12: Toe change for concept design Figure 13: Toe change through compression of
final design

16. Group F1 15
The front toe arm is fixed between the hub and steering rack, as shown by the AG
concept in Figure 14. The fixing points at the steering rack caused substantial
bump steer in excess of 7°, and the steering rack location in the car meant the
steering column had to pass between the pedals, making them hard to operate in
race conditions. Iterating through for different steering rack fixing locations it was
found, moving the steering rack up to the next chassis member, as shown in Figure
15. This reduced the amount of bump steer to within 2° total change, also moving
the steering column so that it would not hinder pedal operation.
Figure 14: Steering system showing
interaction with steering arm.
Figure 15: Proposed steering arm position.
4.2.5.2. Camber angle
Camber angle dictates the amount of tyre contact
with the ground. Negative camber as shown in
Figure 16 will decrease straight line grip but
increase cornering grip as it counteracts tyre roll
generated by centrifugal forces when cornering. The
following formula can be used to approximate the
camber angle (θC) required for the wheels to remain
flat with the ground.
𝜃 𝐶 = sin−1
(
2 ∗ 𝑡 𝑐𝑜𝑚𝑝𝑟𝑒𝑠𝑠𝑖𝑜𝑛
𝑇𝑊
) = sin−1
(
2 ∗ 25.4[𝑚𝑚]
1260[𝑚𝑚]
) = 2.31˚(18)
The graph in Figure 17 represents the above equation plotted for 25.4mm jounce
and rebound. The optimum camber angle was set by finding the wheel displacement
(trc) caused by the maximum cornering load (Wfr), using Equations 19-20, and
extrapolating the camber angle from Figure 17.
𝑊𝑅 𝑐 =
0.5 ∗ 𝑊𝑓𝑟
𝑡 𝑚𝑎𝑥
=
0.5 ∗ 3952.5[𝑁]
25.4[𝑚𝑚]
= 77.8 [
𝑁
𝑚𝑚
] (19)
Steering
Column
Figure 16: Positive vs negative
camber (Blueriverfleet, 2015)
Steering
Column

17. Group F1 16
𝑡𝑓𝑐 =
𝑊𝑅 𝑐 ∗ 𝑡 𝑚𝑎𝑥
𝑊𝑅
=
77.8 [
𝑁
𝑚𝑚
] ∗ 25.4[𝑚𝑚]
48.7 [
𝑁
𝑚𝑚
]
= 40.5[𝑚𝑚](20)
At 40.5mm the camber angle for maximum tyre contact is -1.36˚. Based on this
value a camber graph shown in Figure 18 has been produced, the total change in
camber is significantly lower than if it were left at 0˚.
Figure 17. Camber angle for maximum tyre
contact.
Figure 18. Camper through compression
with optimised static angle.
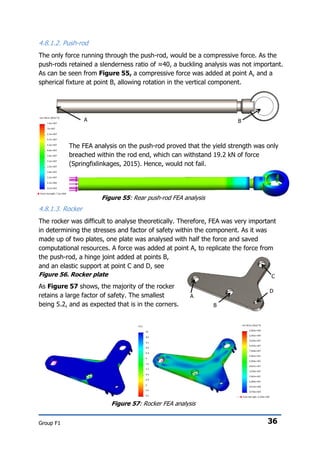
4.2.5.3. Kingpin inclination and scrub radius
The kingpin inclination and camber angle are the only two properties able to alter
the scrub radius, which should be kept between 0 and 10mm to prevent torque steer
(Theander, 2004). An effect that occurs if forces through braking or accelerating are
not the same either side of the car, such as in the event of cornering, a higher scrub
radius will cause greater torque steer.
The kingpin inclination does not change through compression as it is fixed in the
geometry of the hub. Its primary function is to aid the steering’s return to neutral as
the wheel hub rotates about the upper and lower mounting points that form the
kingpin inclination. If the kingpin inclination is too large, it will cause heavy steering
that tries to snap back to neutral. The kingpin also affects the scrub radius, the
larger the kingpin, the lower the scrub radius.
Initially the scrub radius was close to 40mm, as such the kingpin was set to the
maximum value of 8˚. Further alterations, which are covered in Section 4.4. Re-
iteration, Alterations & Design Development, had to be made to the hub and
brake calliper to reduce this value to 11.3mm. This is still larger than ideal, but a
compromise to prevent increasing kingpin inclination or camber angle further.

18. Group F1 17
4.2.6. Roll Centre and Instant Centre
The ride height, wishbone length, and wishbone inclination all affect the location of
the cars instant centre and roll centre, as shown in Figure 19. The instant centre is
the theoretical position at which the wishbones pivot around. The roll centre is then
directly proportional to the instant centre height above the ground. FIA define the
roll centre as "The point in the transverse vertical plane through any pair of wheel
centres at which lateral forces may be applied to the sprung mass without producing
suspension roll" (Technical F1 dictionary, 2014). Therefore, the difference between
the centre of mass and the roll centre forms a moment arm that dictates the amount
of roll the car will undergo when cornering (Technical F1 dictionary, 2014).
Figure 19. Roll and instant centre locations. (Theander, 2004).
The AG concept used horizontal upper wishbones which caused a high roll centre,
and the lowest chassis point off the ground was 85mm, meaning even under full
compression the car was still quite high compared to many competitive FSAE cars. It
was decided to keep the mounting points at the hub and chassis the same, and
lower the car by 30mm. This required a reduction in the lower wishbone length and
an inclination of the upper wishbone which brought the roll centre height, to centre
of mass distance down from 110mm to 12mm. The roll centre was calculated by
representing the lengths and positions of the wishbones on a graph, Figure 20.
This meant the linear regression equations of each wishbone could be solved to find
the point at which they intersect, representative of the instant centre. The roll centre
was determined using the roll centre position at half of the track width, to be
283.5mm at the rear, and 266.4mm at the front.

19. Group F1 18
Figure 20: Concept wishbone arrangement Figure 21: Final wishbone arrangement
4.2.7. Stresses
Individual components were evaluated for their stresses to understand how large
their dimensions would have to be to withstand the forces going through them. The
pushrod was analysed first. Setting assumed dimensions for length, inner and outer
radii, the CSA and second moment of area could be found.
𝐼 =
𝜋∗(𝐷 𝑜
4−𝐷𝑖
4
)
64
(21) 𝐶𝑆𝐴 =
𝜋∗(𝐷 𝑜
2−𝐷𝑖
2
)
4
(22)
A buckling and crushing analysis were carried out using Euler and Rankine methods.
The radius of gyration and slenderness ratio were found by using Equations 23-24:
𝑘 = √
𝐼
𝐶𝑆𝐴
= 0.0054 (23) 𝑆 =
𝐿
𝑘
= 49 (24)
The allowable crushing load was then found by Equation 25:
𝐶𝑐 = 𝑐 ∗ 𝐶𝑆𝐴 = 57 𝑘𝑃𝑎 (25)
The buckling load was then calculated by Equation 26:
𝐶 𝑏 =
𝑛 ∗ 𝜋 ∗ 2 ∗ 𝐸 ∗ 𝐼
𝐿2
= 154 𝑘𝑁 (26)
The Rankine load was calculated using Equation 27:
𝑅𝐿 =
1
1
𝐶𝑐
+
1
𝐶 𝑏
= 42 𝑘𝑁 (27)
This proved well above the load that would be applied through the pushrod, a
bending stress analysis was carried out next. This was done by Equations 28-30:
𝑇 = 𝐹 ∗ 𝑑 (28) 𝑦 =
𝐷 𝑜
2
(29) 𝜎 =
𝑇∗𝑦
𝐼
= 4 ∗ 108
𝑃𝑎 (30)

20. Group F1 19
The stress was found by using goal seek to find an outer radius for a factor of safety
of 2, as the inside radius was fixed by the M12 bolts that were used. The same set
of equations could be carried out for both, front and rear push-rods, as well as the
front, rear, upper and lower wishbones. Although, the forces going through each
component varied due to shape and positioning. Trigonometry and moment
calculations were used to find how the forces were applied to each component. For
the plates that support the push-rods, the stress was found by Equation 31:
𝜎 =
6 ∗ 𝐹
4 ∗ 𝜋 ∗ 𝑡2
∗ ((1 + 𝜈)𝑙𝑛 (
𝐷
2
𝐶𝑆𝐴
) + 1) = 108
𝑃𝑎 (31)
4.2.8. System Response
To obtain an understanding of how the proposed suspension design would react to
going over a bump, a first order analysis was carried out, using a method adapted
from Kyte (2015). However, rather than assuming values for spring rate and damper
coefficient, calculated values were used instead. Spring rate can be seen by
Equation 32, whereas damper coefficient was calculated using Equations 33:
𝐶𝐷 = 2 ∗ √𝑆𝑅 ∗ 𝑚 (32), 𝐷𝐶 = 𝐶𝐷 ∗ 𝜁 (33)
Figure 22: Graph showing first order suspension system response settling time
ζ was assumed to be 0.7 as an ideal value for FSAE cars (Davis et al., 2012). Then a
graph was plotted to graphically visualise how the suspension would respond, this
was done for both front and rear suspension set ups. To determine a better analysis
of the response, a second order analysis was carried out in MatLab as can be seen in
section 4.8.2. MatLab.
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0 0.2 0.4 0.6 0.8 1 1.2
Distancex(m)
Time (s)
Suspension Response
Front Ground Displacement
Front Suspension Displacement
Rear Ground Displacement
Rear Suspension Displacement

21. Group F1 20
4.3. Material selection
There is a vast choice for materials that could be used within the suspension system.
However, there are constraints that must be used to quantify which material would
be the best selection for this project. These constraints include cost and mass
limitations, and the suspension must be able to be worked on by the formula
student team.
Composite and plastic materials were not chosen due to their cost and
manufacturability; this decision led the group to only utilise materials commonly
used for vehicle suspension.
The material selection for any bought in components would not be considered in this
section. It would be deemed that the manufacturer would have undergone many
design procedures to ensure that the components would be of a standard that meets
or surpasses the requirements of the group. The group would therefore have to
ensure that any bought in components are specified correctly.
By searching CES EduPack on level two, all of the metals (ferrous & non-ferrous)
could be compared directly with respect to cost, density and strength. To narrow the
selection down, the elimination of materials that would be inappropriate was
required. This meant removing materials where the cost is far too expensive and the
density to strength ratio would yield no benefit over other materials.
By eliminating the materials that didn’t exceed yield strength of 100MPa a reduced
selection of materials presented, which can be seen in Figure 23.
Figure 23: Level 2 CES EduPack search, metals with yield strength over 100MPa

22. Group F1 21
A level two search narrowed material selection to aluminium and steel. A
spreadsheet that was used to determine the forces, was modified to include the
volume of material, a mass for a component could be determined using a direct
comparison, see Table 1.
Table 1: Extract from calculation spread sheet showing for a comparable load there
is no weight saving using aluminium
Table 1 highlights from the calculation spreadsheet that for a comparable load there
are no benefits from using aluminium. To make a push-rod from either aluminium or
steel, equal in length and capable of withstanding an equal force; the aluminium rod
would need to be a lot thicker in diameter; this increase in size would make the two
masses similar. Considering these points and with cost being an important factor;
the cheaper steel is the more viable choice.
A more in depth search on level three yielded a large selection of materials, so to
narrow this search down further an inspection of all materials and their typical uses
was used to reduce the selection to eight possible choices shown in Table 2.
Table 2: CES EduPack level search of steel that has a typical use of automotive suspension
These high strength low alloy (HSLA) steels are described as offering high-energy
absorption capacity and fatigue strength (Granta Design, 2014). EduPack also states
that these materials are particularly appropriate for automotive suspension systems.
Using this data the team decided the material selection should be HSLA steel YS550;
offering a cheap price for a yield strength of 550-650 MPa.

23. Group F1 22
HSLA YS550 was only available in sheet form. Therefore, it was decided to use AISI
4140 which has similar material properties, shown in Figure 24, and is available in
tube form.
Figure 24: Yield strength comparison for HSLA YS550 (Red) and AISI 4140 (Yellow)
When sourcing steel suppliers the material AISI 4140 was found to not be available
in steel tubing at the sizes required by the calculations. In the search process, a
steel grade of E355+C kept occurring in the required sizing. An investigation into the
material properties found the yield strength to be the same as original YS550 that
was used in the calculations.
Tenaris has a steel tube of dimensions of 15mm OD with a wall thickness of 2mm in
a grade of E355+C (Tenaris 2015). The Tenaris website doesn’t give details of price
for the steel tube, therefore Steel Tubes Direct has been used to give an estimate of
how much the tube would cost at approximately £33 for each length of 5.64m (Steel
Tubes Direct 2015).

24. Group F1 23
4.4. Re-Iteration, Alterations & Design Development
An initial design was developed to integrate a push-rod mechanism into the
suspension system. However, the initial design did not allow enough freedom of
movement within the suspension system. As well as this it induced a bending
moment on the spring and damper system. Therefore, a complete revamp of the
orientation of the design was made, moving the springs from an angled position, to
an upright position, see Figure 25.
Several parts of the design were altered throughout the process. This was either due
to FEA results highlighting failures, components were physically interacting too much,
or to optimise suspension geometry.
4.4.1. Rocker
Figure 25: Spring and damper reposition
Shocks moved
to vertical
position
More freedom of movement
General shape redesigned to accommodate for further movement of
components. Two plate design to reduce weight, and allow certain fixtures.
Connection points altered to allow for ball joints,
enabling further freedom of movement.
Figure 26: Rocker geometry change

25. Group F1 24
4.4.2. Push-rod
4.4.3. Wheel Hub
4.4.4. Anti-Roll Bar
The initial idea for spring position within the rear set-up, was to be positioned
horizontally towards the rear of the car, this did not allow the system to move in
tandem, when being operated through the SolidWorks CAD model. Therefore, to
allow the necessary movement, the springs were moved into a vertical position, see
Figure 29. This meant that the design of the anti-roll bar had to be completely
changed. This change also allowed the ability to make the anti-roll bar out of the
same material as the pushrod, as well as the wishbones, thus reducing
manufacturing costs.
Outside diameter largely reduced, due to incorrect calculations. No bending through push-rod.
Inside diameter remained the same to ensure M12’s could be used throughout assembly.
Figure 27: Push-rod geometry change
New connection points to allow for smaller calliper
to be attached
Off centred connection to allow kingpin inclination.
Off-centre connection point to allow drivetrain clearance
Filleted areas to reduce stress concentrations
Figure 28: Wheel hub geometry change

26. Group F1 25
4.4.5. Brake Calliper
From the calculations in section 4.2.5 Suspension Geometry, the maximum
kingpin inclination was set and the scrub radius was still 30.6mm, approximately 3x
the upper limit. The concept CAD model was analysed, to see if the scrub radius
could be reduced. It was noticed that the brake calliper used for the concept car was
a lot wider than other competitive callipers, which increased the scrub radius.
Therefore, it has been decided that the current AP Racing calliper, will be exchanged
for a Wilwood racing calliper, also popular within FSAE racing events. This would
allow the wheel hub to sit 19.3mm further into the wheel; reducing the scrub radius
to 11.3mm.
4.5. Manufacturing Methods
4.5.1. Hub
The hub is to be manufactured by sand casting. There was an argument for the
hubs to be machined from an ingot but this would generate a lot of waste. The
primary reason to choose sand casting over other methods of casting is purely down
to cost. The price of making the mould is cheaper than other casting moulds
especially for small runs (CPM Industries, 2014).
85.8mm
m
66.52mm
Figure 30: Change in brake calliper
New design allowed the
same loop joints used in
other parts of the assembly
to be incorporated,
simplifying assembly.
New design changed to
bar, reducing parts, and
enabling the use of the
same material as pushrod
and wishbones.
Figure 29: Anti-roll bar geometry
change

27. Group F1 26
The tolerance for this manufacturing method is approximately 0.3mm,
surface finish is classed as fair to good and the thinnest section that can be
cast is around 2.5mm (CPM Industries, 2014). The production of the hubs
could be done in two ways the first could be to outsource the work to a
company that would be able to produce the parts, or they could be done
within the university.
Outsourcing of the manufacture does highlight unknown costing and
without directly speaking to a vendor, it would be difficult to ascertain the
actual cost. However, an estimate of £720 (as of 08/04/2015) for the four
hubs has been achieved using an online source Custompart.net. The quote
is for aluminium A356, the UK equivalent is LM25 a die casting aluminium
alloy that has a high corrosion resistance and is commonly used in road vehicles
(Norton Aluminium, 2009).
Using the in house method would involve the production
of a pattern for the cope and drag, sourcing of adequate
green sand for the sand cast and the use of furnace to
melt the aluminium for pouring. Once the hubs have been
cast there is a need for post processing to ensure that net
shape is obtained accurately, due to the lower quality
surface finish associated with this method of production
(Triad Magnetics, 2015).
The in house production would only be possible if all health & safety precautions can
be met, along with relevant risk assessments it must be a priority to maintain the
safety of all students, staff and equipment.
4.5.2. Adjustable Rods
All of the adjustable rods (push-rod, anti-roll bar and toe arm) would be
manufactured from steel tubing cut to desired length. Utilising a tap, a thread can be
made on the inner diameter, to allow assembly with the loop joints.
The flats that are required for spanner locations on adjustable rods, allow for
adjustments without the need to disassemble the suspension, see Section 4.7.3.
Push-rod, and would be produced using a
surface grinder.
4.5.3. Wishbones
The wishbone manufacture would involve
cutting the steel tubing to desired length,
machining the connecting end piece to size
with a recess of equal size to the outer
diameter of the tube and welding to fix into
Figure 32: Estimate for the wheel
hub manufacture from custompart.net
Figure 33: Rear lower wishbone
Steel tubing
Steel plate
End piece
Figure 31: Rear
wheel hub

28. Group F1 27
place. The chassis side of the wishbones will need to be tapped to ensure that the
M12 bearing fixings will screw into the end pieces.
In the design there are plates used as cross members on the lower wishbones these
will be cut to size from a sheet of steel. The approximate price for a sheet 500mm x
500mm and 6mm thick would be £16 (Buy Metal Online, 2015).
Using the University water-jet cutter would ensure accurate dimensions are obtained
without affecting material properties and adding any extra hardening along the edge
or heat affected zones (KMT Waterjet, 2015). Proper post cutting care will have to
involve washing, cleaning and lubricating of the steel to prevent rusting as this
process will involve a higher risk of oxidation.
The design shows connection points on the chassis and the lower wishbone support
plate, these will also be made from the same steel sheet and also cut with the
water-jet cutter. These parts can be welded into position the same as the support
plates.
4.5.4. Rocker
The rocker will be constructed from the same steel sheet as the
wishbone plating. Utilising the University’s water-jet cutter would
ensure accurate dimensions, and it would not struggle with the
complex shape. This also means that the CAD file could be sent
straight to the water-jet, rather than engineering drawings being
followed by a technician.
The two plates will be connected by nuts and bolts through bearing
joints, that will ensure the rocker will not come apart, as well as the
two plates remaining an equal distance from each other.
4.5.5. Bushings
To ensure the rod ends remain in place there is a need for bushings,
see section 4.7. Detail Design. The manufacture of the bushings
would be completed in house using a bought in steel tube OD 14mm,
ID 11mm (Steel Tube Direct, 2015). The tube can be turned on a
lathe to achieve a 12mm OD along 8mm of the length to match the
ID of the rod end; where it will be inserted. The remaining bushing
length will be cut to maintain an equal space of the rod end in the
chassis and hub fixings.
4.6. Imported Parts
Some components did not need to be completely bespoke to the design, off the
shelf items were chosen to save in-house manufacturing costs, as well as provide
quality assurances.
Figure 34: Rocker
14mm
11mm
12mm
Figure 35: Bushing
8mm

29. Group F1 28
4.6.1. Dampers
To ensure the suspension system would be
adequate for racing, specifically sold FSAE
dampers were chosen to be imported in. A
choice of two dampers were available, a budget
cost effective shock, and a double adjustable
shock. In attempt to remain as competitive as
possible, the double adjustable shock was
chosen. It enables more thorough optimisation
of the damper. A set up can be theoretically
calculated. However, as there are too many
parameters that effect the performance of the
shock, such as tire pressure, lowering of vehicle
and even driver style, testing and optimising
would have to be carried out to ensure the set
up was correct for each race (Nelson, 2009).
4.6.2. Springs
The springs supplied by KAZ technologies, did not provide a spring
stiff enough for the suspension system design. Therefore, one was
bought in from TF tuned, at the correct length to fit the bought in
damper. This allowed the travel of 50.8mm stated by FSAE rules,
as well as the stiffness to accommodate the suspension design.
4.6.3. Rod End
To enable free movement at the joints, a ball joint mechanism was
decided to be incorporated into the design. This would consist of a
spherical bearing, wrapped by a loop joint, see Figure 38. The supplier
Springfix Linkages specifically supply rod ends for suspension systems, as
well as state the M12 loop joint can withstand up to 19.2 kN of force, well
over the force applied to the suspension system.
4.6.4. Nuts, Bolts & Fixings
The bolts used for the rocker will be M12, 70mm high tensile hex
heads. This allows enough clearance for a nut to be screwed on to
keep everything in place. Although some bolts will require being
shorter, they can simply be cut down before assembly.
However, on the rod ends, M10, 70mm high tensile hex head bolts
will be used, accommodated with machined bushings either side of
the loop joint to stop vertical movement.
Double Adjustable
Single Adjustable
Figure 36: Damper selection
comparison
Figure 37:
Imported
springs
Figure 38:
Imported rod ends
Figure 39: 70mm M12
partial threaded bolt

30. Group F1 29
Nylock nuts will be used on all M10 bolts so that they efficiently
stay locked in place. Also, to reduce the effect of the excessive
vibration that will inevitably be induced by the nuts and bolts
from harsh driving conditions.
Standard M12 nuts will be used on the rod ends to lock
components such as the push-rod in place, dependant on the
optimised position.
4.6.5. Washers
Standard flat washers will be used where any nuts and bolts make contact with the
chassis and other components, protecting them from damage by evenly distributing
the applied pressure. The design will require both M10 and M12 washers to
accommodate for the two different size bolts being used.
Standard flat washers are made to a tolerance according to BS4320 and the bolts
being used have a length to accommodate for this range in variance.
4.7. Detail Design
A key part in developing a fully functional
suspension system, is ensuring that all the
components stay sufficiently
fixed together to deal with the
harsh conditions of a racing
environment. However, as
suspension systems are often
changed and regulated
throughout different
competitions within a racing
event, the ability to alter certain dimensions of the suspension
will also have to be incorporated into the design. Therefore,
identifying what parts of the suspension will remain fixed, and
what will have to be altered played an integral role within putting
the model together.
Where components such as the wishbone, attach to the chassis,
the rod ends should be able to move around its spherical bearing.
Although, should not be able to move vertically along the pin in
which the rod end is attached to, see Figure 41. To
accommodate this movement, bushings will be incorporated
either side of the rod end to stop vertical movement, and will sit
flush within the clevis joint, see Figure 42.
Figure 40:
M12 Nylock nut
Figure 41: Bushing locations
Clevis
Joint
Figure 42:
Bushing and rod
end assembly

31. Group F1 30
4.7.1. Lower Wishbone
Rod ends will be attached to the lower wishbone, at the control arms and end piece.
Locking nuts will be used to allow adjustment for different race conditions and to
prevent the rod from loosening.
The lower wishbone will be mounted to the chassis using the standard rod ends,
which will be screwed into the threaded end of the control arms and end piece,
before being placed in the chassis clevis joint, and hub mounting, secured with a
M10 bolt and nylock nut. The pushrod will be fixed to the pushrod supports, using a
rod end on the pushrod end, with an M12 bolt and nylock to hold it in place.
4.7.2. Upper Wishbone
The principle is similar to the
lower wishbone. The control
arms are welded to the end piece
with rod ends at each end
secured with M12 locking nuts.
The alteration of the wheel
camber is controlled by adjusting
the distance of the hub
connection to the wishbones. A
locking nut, that will be moved
along the inside of the wishbone
will allow for the alteration of the wheel camber.
4.7.3. Push-rod
The push-rod is a comparatively simple assembly. It is a length of steel tubing with
rod ends at each end. Locking nuts are used at each end to secure that it will not
loosen or adjust under vibration or toque. However, to ensure alterations can be
Control arms
Locking nuts
End piece
Pushrod supports
Figure 43: Exploded view of rear lower wishbone
Weld points
Rod end to
adjust camber
angle
Figure 44: Exploded view of rear upper wishbone

32. Group F1 31
made to the length in which the push-rod attaches, opposing threads will be utilised
at opposite ends. Therefore, by turning the push-rod itself, will entice the rod ends
to move either towards each other, or away from each other.
To ensure that damage is not caused to the push-rod by tooling,
flats will be incorporated into the surface. This would allow a spanner
to wrap around the push-rod enabling an easy torque rotation.
4.7.4. Positioning arm & Anti-roll bar
Similar to the pushrod, two opposing
threaded rod ends will be secured with
locking nuts to ensure correct position. The
flats along the surface will also have to be
utilised to ensure easy rotation, in which will
alter the toe angle of the wheels. The anti-
roll bar will also be assembled in the same method as the push-rod and positioning
arm.
The flats incorporated into the
components are placed specifically
nearer the thread. Therefore, will have
the least effect on the stress within the
components, as well as allow easy
access for tooling access.
4.7.5. Rocker
As previously explained the rocker is
formed of two water cut sections of steel sheet joined by M12
nylocks and bolts, as well a 6mm pin to accommodate the
damper. It will be mounted to the push-rod, anti-roll bar,
chassis and the damper. This part will not need any alteration.
However, access may be needed to allow replacement, or
adjustment of other parts.
Locking nuts, to lock optimised geometry
in place
Opposing threads
Figure 45: Push-rod assembly Flattened
surface
Figure 46: Example of
flats on components
Figure 47: Positioning arm assembly
Flat
s
Figure 48: Flats locations
Figure 49: Rocker
assembly

33. Group F1 32
4.7.6. Hub
Although not a sub assembly it is a vital part as provides the
connection between the suspension components and the wheel and
brake system, therefore there are a lot of connection points on the
hub. Careful consideration has been taken to ensure the 19mm
spanner required for a M10 bolt can be used efficiently. The same
bushings will also be incorporated into the connection points, to
ensure vertical displacement will be restricted.
4.7.7. Springs and Dampers
The rebound rate of the damper can be adjusted via a
dial shown in Figure 51 using a 5mm pin placed into
the holes and rotated. To accommodate for this, the
dampers were placed upside down, allowing enough
clearance to get to the adjustment location.
4.7.8. Full assembly
To rod ends are used to attach the sub-assemblies
to the chassis and hub. A recommended method of
assembly would be to attach the rockers and
wishbone assemblies, then the hub, anti-roll bar
and push-rod. The shocks and springs would be
attached last.
4.7.9. Tolerances
Every part has a dimensional tolerance associated
with it; this is the range of dimension the part will
be in reference to the specified length. The
tolerances for each part are provided within the
drawing pack for each part.
It is important to assess what impact these tolerances may have on the performance
of the design. The control arms have a tolerance of ±0.5mm per section, this means
the total variance could be up to 2mm across a wishbone. This sort of discrepancy
could alter operating conditions such as toe angle and camber depending on the
geometry. However, the geometry is designed so it can be altered, meaning that any
dimensional discrepancies will not have an effect on the performance of the
suspension system as they can be altered manually. For the flat sections of the
pushrod and other components, tight tolerances of 0.1mm will be used to ensure the
structural strength of the components will remain.
Figure 50: Rear
hub with bushings
Figure 52: Rear left assembly
Adjustment mechanism
Figure 51:
Rebound adjustment

34. Group F1 33
4.7.10. Altering Geometry
The rod ends used, denote a fine pitch thread (Springfixlinkages, 2015), comparing
with the chart from (EngineeringToolbox, 2015) it was found a full rotation of a rod
end, would produce 1.5mm of travel. The suspension geometry can be altered to
give the optimum performance for each race event by adjustments to the overall
wishbone, and toe arm lengths. This is achieved by screwing the rod ends further
into, or out of, the control arms and end pieces. Alteration can be made at both
ends to ensure the loading remains evenly distributed. However, the maximum
visible thread distance should not exceed 18mm (Aurora bearing, 2015) to prevent
damage to the threads. Table 3 shows the adjustments achievable with one full
turn of the rod end. The values were obtained using the Excel Goal Seek function in
the geometry spreadsheets, to work back from the final part lengths to the input
angles and dimensions.
Table 3: Geometry alteration
Part Name: Rod end Adjustment Direction: Adjustment Effect:
Front
Upper
wishbone
One full turn (IN/OUT) Camber change: -
0.4⁰/+0.4⁰
Scrub radius: -
1.1mm/+1.1mm
Lower
wishbone
One full turn (IN/OUT) Track width: -
3.0mm/+3.0mm
Camber change:
+0.4⁰/-0.4⁰
Toe arm One full turn (IN/OUT) Toe angle: +3.2⁰/-3.2⁰
Rear
Upper
wishbone
One full turn (IN/OUT) Camber change: -
0.4⁰/+0.4⁰
Scrub radius: -
1.1mm/+1.1mm
Lower
wishbone
One full turn (IN/OUT) Track width: -
3.0mm/+3.0mm
Camber change:
+0.4⁰/-0.4⁰
Toe arm One full turn (IN/OUT) Toe angle: +2.8⁰/-2.8⁰
4.8. Simulation Analysis
4.8.1. FEA
In order to give more confidence in the theoretical analysis for the stress applied on
each component, an FEA analysis using SolidWorks simulation was carried out on
each individual component, starting with a mesh independence study. A factor of
safety of 1.5 was deemed to be ideal in attempt to remain as competitive as possible,
by keeping the components light.

35. Group F1 34
4.8.1.1. Wishbones
The wishbone loadings were complex, as they are applied to the plate at an angle,
and the end of the wishbone. However, as the loads on the plate were resultant
forces from the push-rod, an assumption was made that at maximum spring
compression, the push-rod acted as fixed geometry, with dynamic loads applied at
the end of the wishbone. Therefore, any bending forces acting upon the wishbone
would be acting around the push-rod attachment.
The same method was not adopted for the upper wishbone as the push-rod does
not affect it. Therefore, only the spherical fixtures were used with a compressive
force at the opposing end, see Figure 54.
Figure 54: Rear upper wishbone FEA analysis
A buckling analysis was also considered for the upper as the tubes retain a
The majority of stress is located in the
area between push-rod and hub
attachment
Spherical fixtures to allow tilt
Basic Fixture
Bending and
compressive
forces
Figure 53: Rear lower wishbone FEA analysis

36. Group F1 35
slenderness value of ≈ 63. A similar method was carried out to Lee (2014). This
helped highlight the failure cases that could occur upon the wishbone through
buckling. As well as highlighting the factor of safety for each failure case. 10 cases
were analysed throughout the simulation. However, the majority of them retained a
very large factor of safety. Table 4 shows the top 5 failure cases that could occur,
and their individual load factors (factor of safety based on applied load).
𝐵𝑢𝑐𝑘𝑙𝑖𝑛𝑔 𝐿𝑜𝑎𝑑 = 𝐴𝑝𝑝𝑙𝑖𝑒𝑑 𝐿𝑜𝑎𝑑 ∗ 𝐿𝑜𝑎𝑑 𝐹𝑎𝑐𝑡𝑜𝑟(𝐹𝑜𝑆)(34)
Table 4: Showing different buckling cases for upper wishbone
Load
Case
Applied
Load (N)
Load Factor
(FoS)
Buckling
Load (N) Deformed Shape
1 1767 1.6129 2849.9943
2 1767 42.836 75691.212
3 1767 53.525 94578.675
4 1767 83.842 148148.814
5 1767 144.55 255419.85
As the table shows, none of the failure cases breach a factor of safety of below 1.
Load case 1 also is only considered a failure within SolidWorks because the
wishbone has moved from its datum, which in this case is acceptable as it has only
moved about its hinge.

37. Group F1 36
4.8.1.2. Push-rod
The only force running through the push-rod, would be a compressive force. As the
push-rods retained a slenderness ratio of ≈40, a buckling analysis was not important.
As can be seen from Figure 55, a compressive force was added at point A, and a
spherical fixture at point B, allowing rotation in the vertical component.
4.8.1.3. Rocker
The rocker was difficult to analyse theoretically. Therefore, FEA was very important
in determining the stresses and factor of safety within the component. As it was
made up of two plates, one plate was analysed with half the force and saved
computational resources. A force was added at point A, to replicate the force from
the push-rod, a hinge joint added at points B,
and an elastic support at point C and D, see
Figure 56. Rocker plate
As Figure 57 shows, the majority of the rocker
retains a large factor of safety. The smallest
being 5.2, and as expected that is in the corners.
A
B
C
D
BA
The FEA analysis on the push-rod proved that the yield strength was only
breached within the rod end, which can withstand 19.2 kN of force
(Springfixlinkages, 2015). Hence, would not fail.
Figure 55: Rear push-rod FEA analysis
Figure 57: Rocker FEA analysis

38. Group F1 37
Applied force at
back face of hub
Hinge
fixtures
Figure 59: Second order model of the
suspension system
4.8.1.4. Hub
The hub has the most complex geometry.
Therefore, FEA played a strong part in
defining if the geometry was capable of
handling the applied forces.
4.7.1.5. Front
The same analysis was
carried out on the front
suspension set up.
However, as the
components are of very
similar dimensions as the rear, with less forces acting through them, it was clearly
evident that geometry did not have to change within the front set up.
The FEA showed that the components within the suspension system would be able
to withstand the forces acting through them. The factor of safety for the majority of
the components was in excess of the 1.5.
4.8.2. MatLab
The Matlab/Simulink model predicts the
settling time (road holding) of the car after
hitting a bump. The vehicle should not
experience large oscillations, and the
oscillations should dissipate quickly (short
settling time).
To simulate the effects of the car hitting a
bump on the track a 1/4 model, replicating 1
of the 4 wheels was used to simplify the
problem to a 1-dimensional (x direction)
second order spring-damper system, as
shown in Figure 59. This model replicates
the car hitting a 0.01m bump (W=0.01m).
Where the input parameters are shown in Table 4:
Stress concentrations
occur at attachment
points
Majority of the body has
a high factor of safety
Figure 58: Rear wheel hub FEA analysis

39. Group F1 38
Table 5: Input parameters
Property Symbol Units Value Front Value Rear Source
Body Mass M1 kg 25 50 Calculations
Suspension Mass M2 kg 15 15 Calculations
Spring constant of
suspension system
K1 N/m 102732 183695 Calculations
Spring constant of
wheel and tyre
K2 N/m 262000 262000 Kaz Technologies
Damping constant of
suspension system
B1 Ns/m 3541.5 6741 Calculations
Damping constant of
wheel and tire
B2 Ns/m 0 0 Assumption
4.8.2.1 Building the model
This system is modelled by summing the forces
acting on both masses and integrating the
accelerations of each mass twice, to give velocity
and displacement values. This is represented by
Equations 35-36, and the Simulink model by
Figure 60:
∬
𝑑2
𝑥1
𝑑𝑡2
𝑑𝑡 = ∫
𝑑𝑥1
𝑑𝑡
𝑑𝑡 = 𝑥1 … … … (35)
∬
𝑑2
𝑥2
𝑑𝑡2
𝑑𝑡 = ∫
𝑑𝑥2
𝑑𝑡
𝑑𝑡 = 𝑥2 … … … (36)
The system is governed by Newton’s second
Law. Newton's law for each of these masses
can be expressed as Equations 37-38, which
are represented as a block diagram in Figure
61:
1
𝑀1
∑1 =
𝑑2
𝑥1
𝑑𝑡2
… … … (37)
1
𝑀2
∑2 =
𝑑2
𝑥2
𝑑𝑡2
… … … (38)
Force from spring (FK1) is a constant, 𝐹𝐾1 = 𝐾1 (𝑥1 − 𝑥2) as shown in Figure 62.
Figure 61: Block diagrams
representing equations 37 and
38, respectively.
Figure 60: Block diagrams
representing equations 35 and
36, respectively.

40. Group F1 39
Figure 62: Block diagram representing K1 in terms of displacement.
The force from damper 1 (𝐹𝑏1). Is expressed as 𝐹𝑏1 = 𝑏1 × (𝑣1 − 𝑣2). As shown in
Figure 63.
Figure 63: Block diagram including damping force of damper 1
The force from Spring 2 (𝐹𝑘2) acts only on Mass 2, but depends on the ground
profile, W. This is expressed as 𝐹𝑘2 = 𝑥2 − 𝑤. As shown in Figure 64.
Figure 64: Block diagram including the force from spring 2
The force from damper 2 (𝐹𝑏2) can be expressed as 𝐹𝑏1 = 𝑏2 × 𝑣2 −
𝑑𝑊
𝑑𝑡
. As shown
in Figure 65

41. Group F1 40
Figure 65: Block diagram including the force from damper 2
Since the distance (x1 – W) is very difficult to measure, and the deformation of the
tire (x2 –W) is negligible, the distance (x1 – x2) is the output. To view the output (x1
– x2) a scope is used to analyse the system response in terms of displacement. To
extract forces from the simulation, the acceleration of the wheel in the direction of
the body of the car can be obtained using the acceleration output as shown in the
final Simulink block diagram, as shown in Figure 66.
Figure 66: The final model used to analyse system response to a 0.01m bump
Using the inputs from Table 4, the model produced a system response, in terms of
displacement for the front wheel as shown in Figure 67, and acceleration Figure
68.

42. Group F1 41
Figure 67: Displacement response for the front wheel hitting a 0.01m bump
Figure 68: Acceleration response for the front wheel hitting a 0.01m bump

43. Group F1 42
The model produced a system response, in terms of displacement for the rear wheel
as shown in Figure 69, and in terms of acceleration in Figure 70.
Figure 69: Displacement response for the rear wheel hitting a 0.01m bump
Figure 70: Acceleration response for the rear wheel hitting a 0.01m bump

44. Group F1 43
Table 6 shows the values obtained from the Simulink plots.
Table 6: Values extracted from the Simulink plots
Property Unit Source Value Front Value Rear
Displacement (x1 – x2) m Simulation 0.0048 0.0039
Settling Time s Simulation 0.3 0.4
Acceleration of wheel to body m/s2
Simulation 50.7 34.5
Mass of ¼ of body kg Calculation 25 50
Force acting through system N Newtons 2nd
Law 1267.5 1725
The displacement plots show rapid settling time, this indicates the suspension
system will effectively absorb and dissipate the oscillations after hitting the bump.
The maximum oscillation the car will experience from the bump is 4.8mm, this is
appropriate for the need of the car since the 0.01m has been absorbed and not
affected the driver. The maximum force acting on the car in this situation is 1725N;
this is less than the forces experienced by the car at maximum cornering speed.
Therefore, the system has already been designed to withstand the 0.01m bump.
One issue when trying to model the suspension system was trying to find a suitable
solver to give reasonable outputs. Simulink uses ‘ode45’ for its default solver. This
fourth order solver was deemed too accurate for this second order system as the
plots were covered with unnecessary mathematical noise. Trying other solvers, it
was discovered that the solver, ‘ode23tb’ was not only more time efficient but
returned feasible results.
4.9. Environmental Impact
The environmental impacts of fossil fuel powered motor racing are widely debated.
Moreover, this is aimed towards the engine and has no direct implications for the
suspension system. Therefore, manufacturing and end of life impacts needed to be
considered. Environmental impacts during the life of the suspension are minimal as
there are no harmful chemicals required for its operation, the only fluids necessary
are for lubrication of rod ends.
It is stated in the FSAE rules that a competing car must undergo a significant design
change every two years, with this in mind there will be an impact to the
environment as some components will have to be redesigned. With the possible
short product life it has been important to consider materials able to be recycled at
the end of their life.
During the manufacture of the components there has been consideration to ensure
of the amount of material to be purchased is not surplus to requirements, and any
offcuts can be recycled.
The suspension system uses two main materials, steel, for the tubing and plates,

45. Group F1 44
and aluminium to cast the hubs. Suppliers of externally sourced component’s and
materials will need to adhere to ethical and environmentally friendly principles. The
E355+C steel is a high strength tensile steel, the environmental impact of steel in
general will be used for this analysis. Tata Steel Construction (2015) provides data
for the carbon and energy impacts of steel products in the UK.
𝑀𝑎𝑠𝑠 𝑜𝑓 𝑡𝑢𝑏𝑒 𝐸355 + 𝐶 = 6.79 𝑘𝑔
𝐶𝑂2 (𝑘𝑔) = 6.79 𝑘𝑔 ∗
0.857𝑘𝑔
𝑘𝑔
= 5.79 𝑘𝑔 𝑜𝑓 𝐶𝑂2(39)
𝐸𝑛𝑒𝑟𝑔𝑦 = 6.79 𝑘𝑔 ∗ 15.42
𝑘𝐽
𝑘𝑔
= 104 𝑘𝐽(40)
𝑀𝑎𝑠𝑠 𝑜𝑓 𝑠ℎ𝑒𝑒𝑡 = 1.82 𝑘𝑔
𝐶𝑂2 = 1.82 𝑘𝑔 ∗ 0.919𝑘𝑔/𝑘𝑔 = 1.67𝑘𝑔 𝑜𝑓 𝐶𝑂2(41)
𝐸𝑛𝑒𝑟𝑔𝑦 = 1.82 𝑘𝑔 ∗ 17.37
𝑘𝐽
𝑘𝑔
= 31.6𝑘𝐽(42)
Steel shows high energy and CO2 values during production which increases
environmental impacts. However, aluminium and steel are widely and readily
recycled. Materials are expected to be recycled at their end of service, making the
end of life environmental impacts of steel and aluminium minimal.
The aluminium hubs will be sand cast. This process is not being performed on a
large industrial scale, the environmental impacts should be considered as the
immediate casting environment. Ventilation will be paramount due to the potentially
harmful gases released during melting. Casting processes require a large amount of
energy and are often inefficient; it is not possible to give an energy consumption
figure as it will vary from foundry to foundry.
4.10. Cost Analysis
The cost analysis involved summing up the amount of imported parts, manufacturing
and material costs to build the suspension system. The initial aim was to keep the
price of the model either the same or below the proposed concept. But, the concept
cost analysis did not include a detailed bill of materials or manufacturing costs; so it
was very unlikely this goal would be met. Also the exchange rate for dollars to
sterling was weaker than last year. Table 8 shows the cost analysis carried out in
order to manufacture the proposed design, using an exchange rate for necessary
parts as of 08/04/15.
Plate Tube
CO2 (kg/kg) 0.919 0.857
Energy (kJ/kg) 17.37 15.42

46. Group F1 45
Table 8: Cost analysis to develop suspension model
Parts Part Names
$ Per
Part $ to £
£ Per
Part /
Pack Quantity
Total Cost
(£)
Damper
7800 FSAE Piggyback
Double Adjustable 750 0.67 502.50 4pcs 2010.00
Spring
Vivid/ Kage Rear Grey
Spring 2/2.25" Stroke 35 0.67 24.98 4pcs 99.92
Steel Tubing 5.64m Tube 65.60 2pcs 131.20
3.05m Tubing for
Bushings 7.91 1pc 7.91
Rocker/
Wishbone Plate 500mm x 500mm x 6mm 16.14 1pc 16.14
Hub Cast Aluminium 268.32 0.67 179.77 4pcs 719.10
Loop Joint R Economy Male Rod End R 4.52 34pcs 153.68
Loop Joint L Economy Male Rod End L 5.32 6pcs 31.92
Bolts M12 x 70mm Hex 7.49 1Pk / 50pcs 7.49
M10 x 70mm Hex 10.31 1Pk / 100pcs 10.31
Nuts M12 Right Thread Nut 6.59 1Pk / 100pcs 6.59
M12 Left Thread Nut 1.08 20 pcs 21.60
M10 Nyloc Nut 3.45 1Pk / 100 pcs 3.45
Washers M10 Flat 3.19 1Pk / 100pcs 3.19
M12 Flat 4.49 1Pk / 100pcs 4.49
Total (£)
3226.99
The hub cost is highlighted in red because if the casting procedure was to occur
within the university campus, a lot of money could be saved. However, as explained
in Section 4.5.1. Hub, all relevant risk assessment and health and safety
precautions must be abided by.
5. Conclusion
The proposed design meets the project aim by being a fully developed operable
suspension system, and complies with the strict FSAE rules and regulations
governing formula student car design, that the product specification was developed
around.
The suspension was designed primarily with SolidWorks, in tandem with calculations,
which caused difficulties when sourcing components from vendors due to sizing
issues. If repeated, the design would be based around the selection of available
materials that meet the design requirements.

47. Group F1 46
6. Recommendations & Advisories
Further work required:
 Steering and drivetrain can be integrated into the design
 Exhaust system requires relocation as it currently exhausts into the
suspension system
 Chassis attachment points will need to added to the base design to
accommodate for the suspension design
 The car will have to go through experimental testing before going into an
event

48. Group F1 47
7. References
2015 Formula SAE Rules. (2014). 1st ed. [ebook] SAE International. Available at:
http://students.sae.org/cds/formulaseries/rules/2015-16_fsae_rules.pdf
Aurorabearing.com, (2015). FAQs - Aurora Bearing Rod Ends, Spherical Bearings &
Bushings. [online] Available at: http://www.aurorabearing.com/technical-faqs.html
[Accessed 2 Apr. 2015].
Bansal, R (2005) A Textbook of Theory of Machines, USA: Laxmi Publications.
Blueriverfleet.com, (2015). Blue River Fleet Service - Shelbyville, IN. [online]
Available at: http://www.blueriverfleet.com/alignment.htm [Accessed 20 Apr. 2015].
Buy Metal Online (2015) 6.0mm / 2 SWG (0.236") - HOT ROLLED, Available
at:http://www.buymetalonline.co.uk/buy-steel-sheet/hot-rolled/6.0mm-2-swg-hot-
rolled.html(Accessed: 16th April 2015).
Carltedt, T. (2014) Sand Casting vs Investment Casting, Available
at: http://info.cpm-industries.com/blog/bid/178170/Sand-Casting-vs-Investment-
Casting (Accessed: 13th April 2015).
Custompart.net (2009) Cost Estimator, Available
at:http://www.custompartnet.com/estimate/sand-casting/ (Accessed: 13th April
2015).
Davis, W, Carney, K, Leith, J, Kirschner, A, Piccioli, D (2012) DESIGN AND
OPTIMIZATION OF A FORMULA SAE RACECAR , Worcester: WORCESTER
POLYTECHNIC INSTITUTE .
Drivealuminum.org, (2015). Sustainability — Drive Aluminum. [online] Available at:
http://www.drivealuminum.org/aluminum-advantages/sustainability [Accessed 20
Apr. 2015].
EngineeringToolbox,. 'Threads - Metric ISO 724'. Engineeringtoolbox.com. N.p.,
2015. Web. 21 Apr. 2015.
Epa.gov, (2015). Life Cycle Assessment (LCA) | Sustainable Technology Research |
US EPA. [online] Available at: http://www.epa.gov/nrmrl/std/lca/lca.html#define
[Accessed 17 Apr. 2015].
Formula1-dictionary, (2015). 'Pushrod-Pullrod'. Web. 7 Apr. 2015.
Granta, Design. CES Edupack. Granta Design, 2015. Print.
Hu, H. (2014) Forged Steel Square - Flat Bar, Available
at:http://www.fuhongsteel.com/forged-steel-square-flat-bar-
2218113.html (Accessed: 31st March 2015).
Kaz Technologies (2015) FSAE Shocks, Available

49. Group F1 48
at:http://www.kaztechnologies.com/fsae/shocks/ (Accessed: 08/04/15).
KMT Waterjet (2015) Metal Cutting, Available at: http://www.kmtwaterjet.com/kmt-
metal-cutting.aspx (Accessed: 16th April 2015).
Kyte, A. (2015). Using Excel Macros.
Lee, H (2014) Mechanics of Materials with SolidWorks Simulation 2014, USA: SDC
Publications.
Nelson, J (2009) Single Vs Double Adjustable Shocks, Available
at:http://www.superchevy.com/how-to/chassis-suspension/0904chp-single-vs-
double-adjustable-varishocks-pros-cons/ (Accessed: 10/04/15).
Norton Aluminium (2009) LM25 (EN 1706 AC-42000) - Aluminium Casting
Alloy,Available at: http://www.nortal.co.uk/LM25/ (Accessed: 16th April 2015).
Popa, C.E. (2005) Steering System and suspension design for 2005 formula SAE-A
racer car, Australia: University of Southern Queensland.
QA1 (2015) Street performance & racing spring rate tech, Available
at:http://www.qa1.net/tech/street-performance-racing-spring-rate-tech (Accessed:
2nd February 2015).
springfixlinkages,. 'Low Cost Rod End - Male'. springfixlinkages. N.p., 2015. Web. 19
Apr. 2015.
Steel Tubes Direct (2015) Round Cold Drawn Seamless Steel Tube | Cold Drawn
Tubes, Available at: http://www.steeltubedirect.co.uk/products/Round-Cold-Drawn-
Seamless-Steel-Tube-Cold-Drawn-Tubes/P100004 (Accessed: 31st March 2015).
Tata Steel Construction, (2015). The carbon footprint of steel | Tata Steel
Construction. [online] Available at:
http://www.tatasteelconstruction.com/en/sustainability/carbon-and-steel [Accessed
17 Apr. 2015].
Tata Steel Europe (2014) Steels for the Aerospace Industry, Available
at:http://www.tatasteeleurope.com/file_source/StaticFiles/Speciality/publications/Tat
a_Steel_Aerospace_Pocket_Book_Aug12.pdf(Accessed: 31st March 2015).
Technical F1 Dictionary (2014) Roll centre, Available at: http://www.formula1-
dictionary.net/roll_center.html (Accessed: 17th April 2015).
Tenaris (2015) Cold drawn seamless steel tubes for mechanical
applications, Available
at: http://www.tenaris.com/shared/documents/files/CB32.pdf (Accessed: 31st March
2015).
Theander, A (2004) Design of a Suspension for a Formula Student Race Car, Sweden:
Aeronautical and Vehicle Engineering Royal Institute of Technology.

50. Group F1 49
Triad Magnetics (2015) Comparing Casting Process, Available
at:http://www.thomasnet.com/articles/custom-manufacturing-
fabricating/comparing-casting(Accessed: 19th April 2015).
University of Michigan (2012) Control Tutorials for Matlab and Simulink, Available at:
http://ctms.engin.umich.edu/CTMS/index.php?example=Suspension&section=Simuli
nkModeling (Accessed: 1st April 2015).