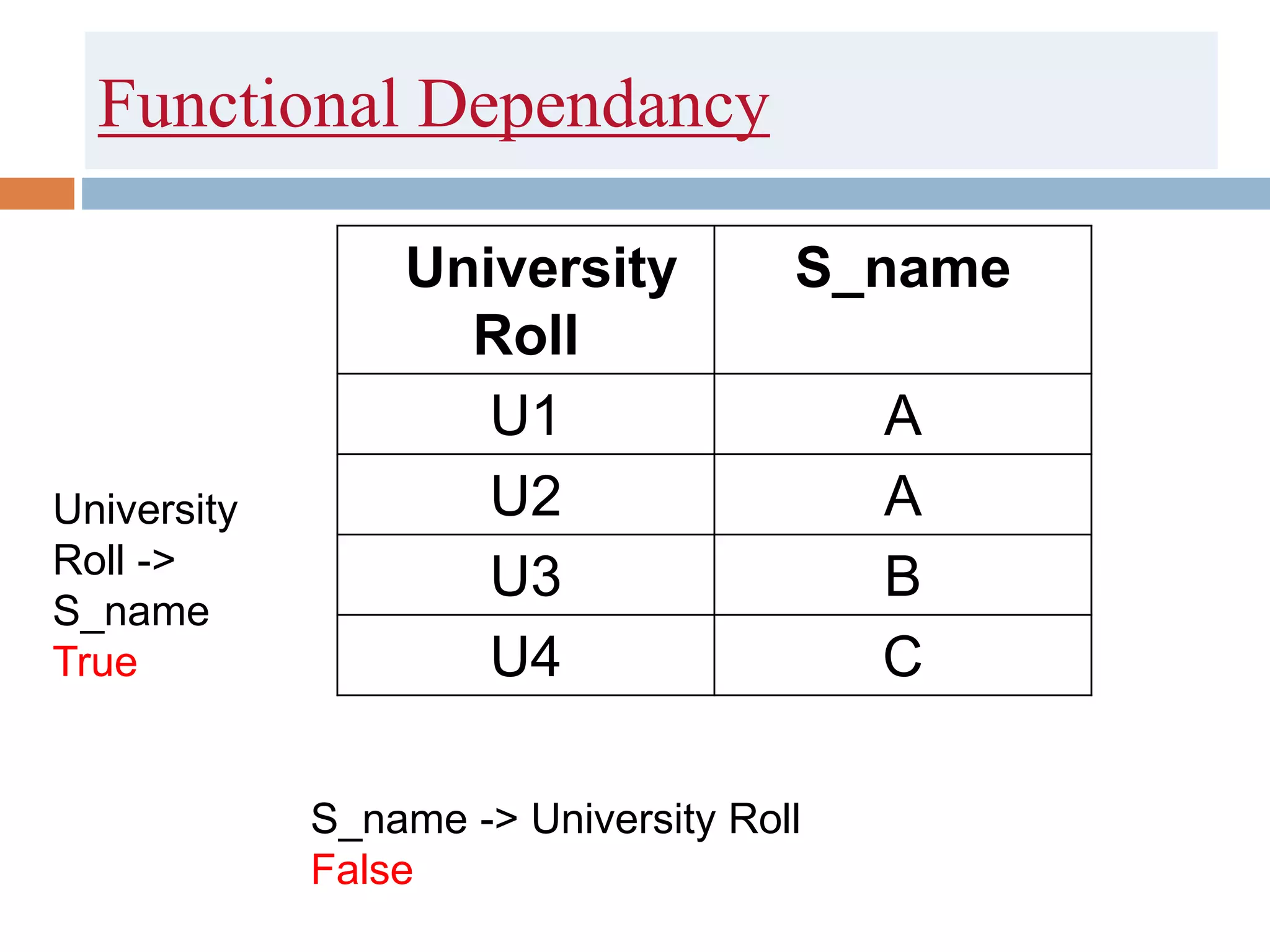
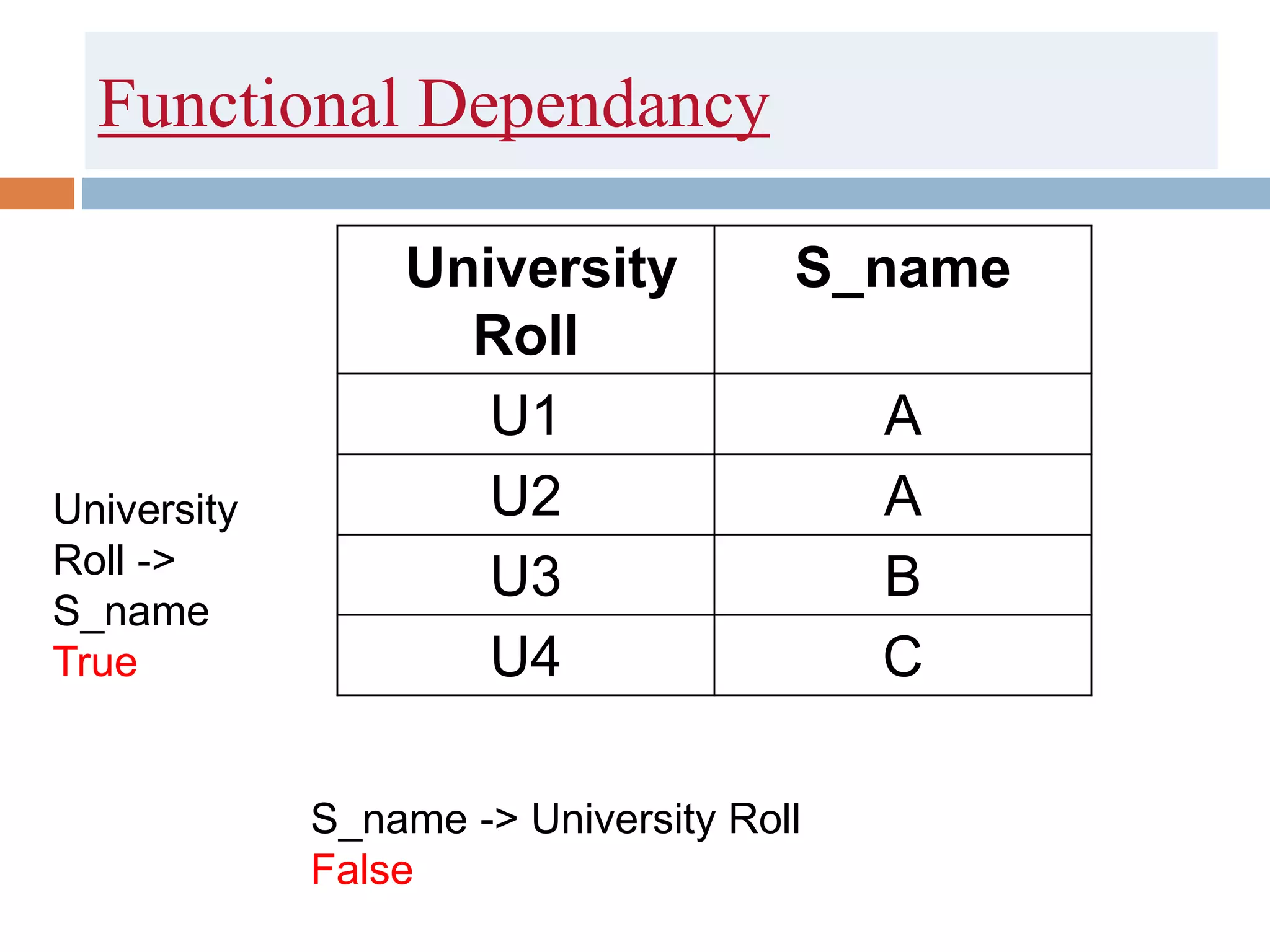
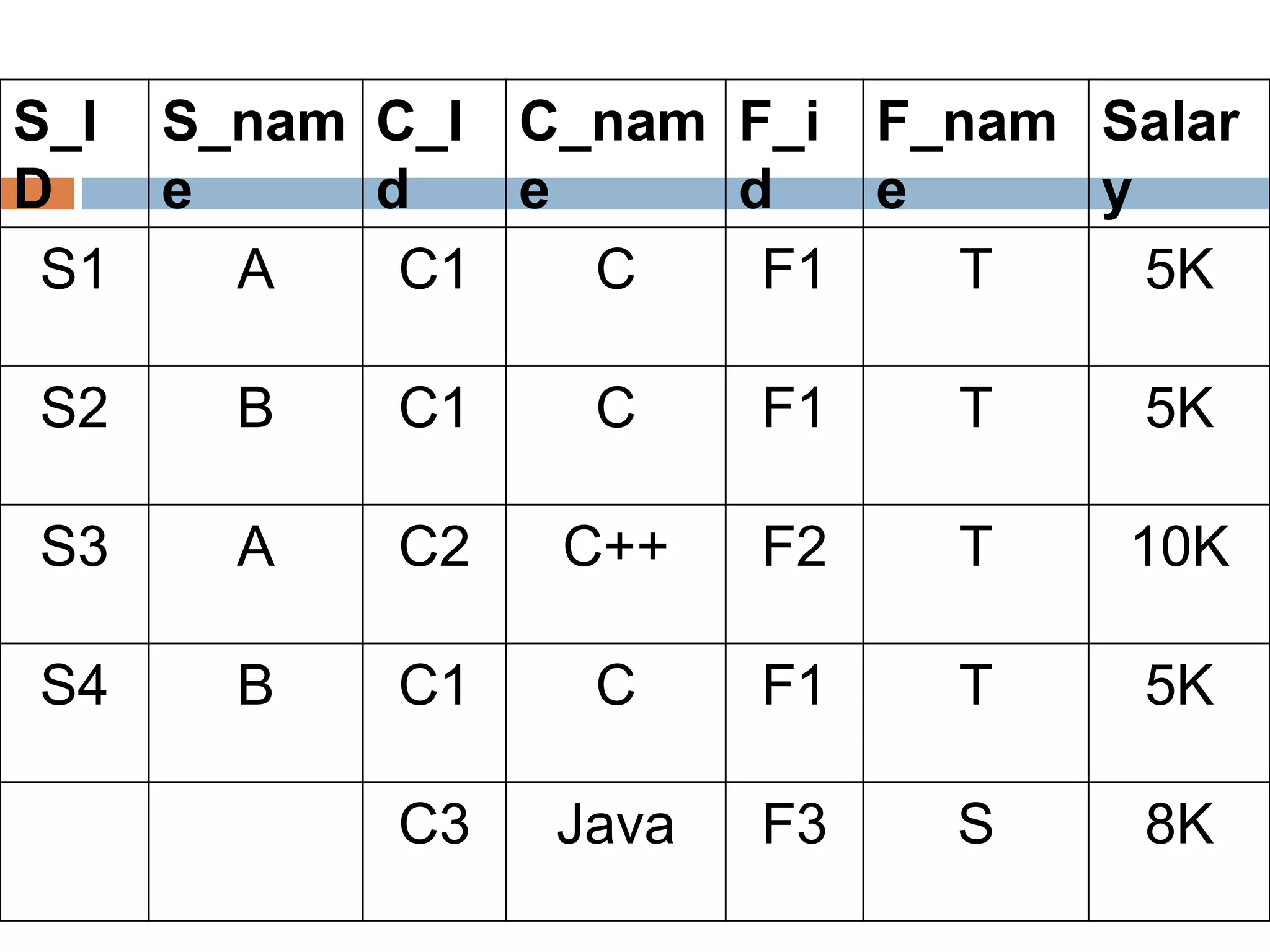
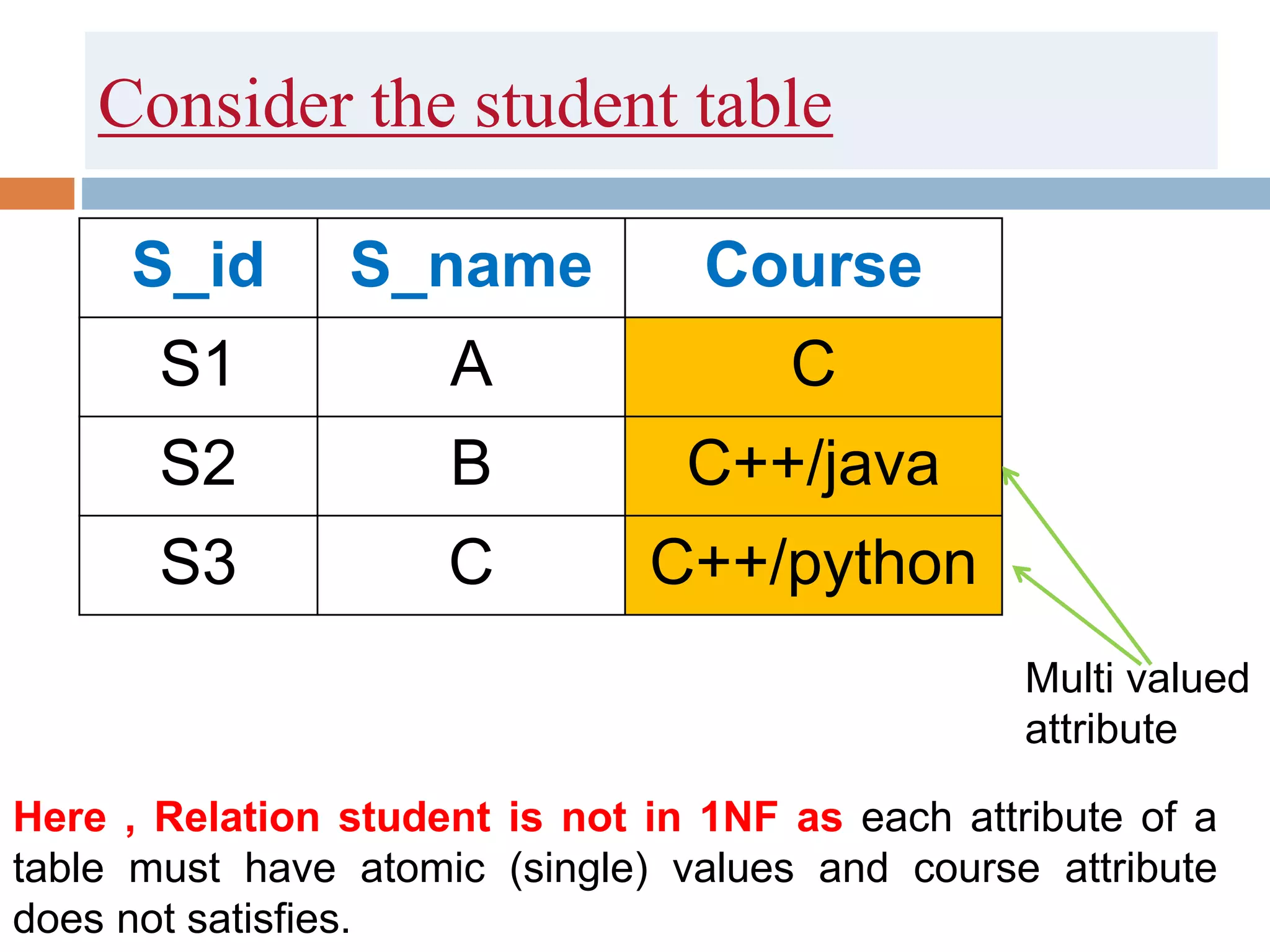
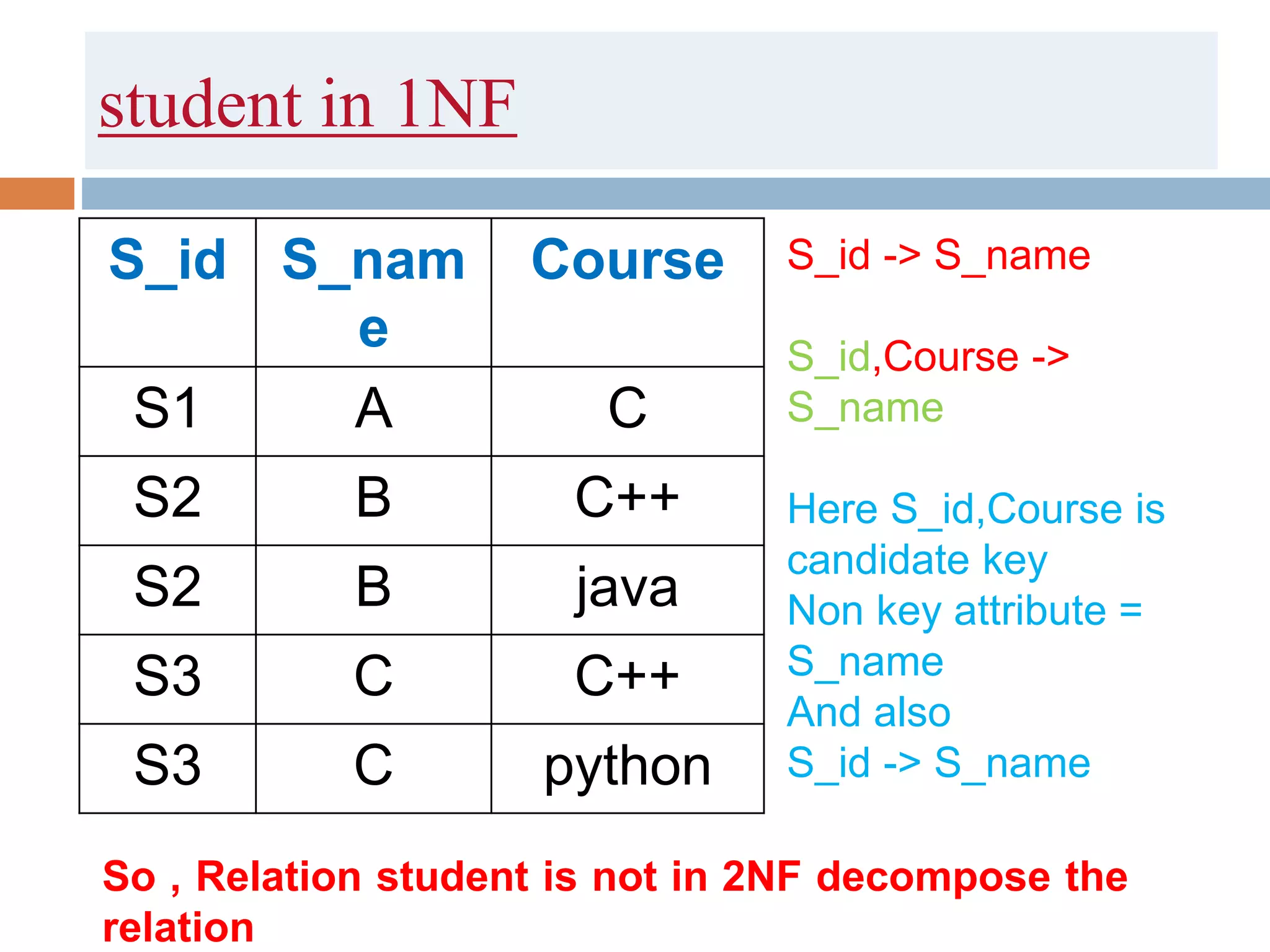
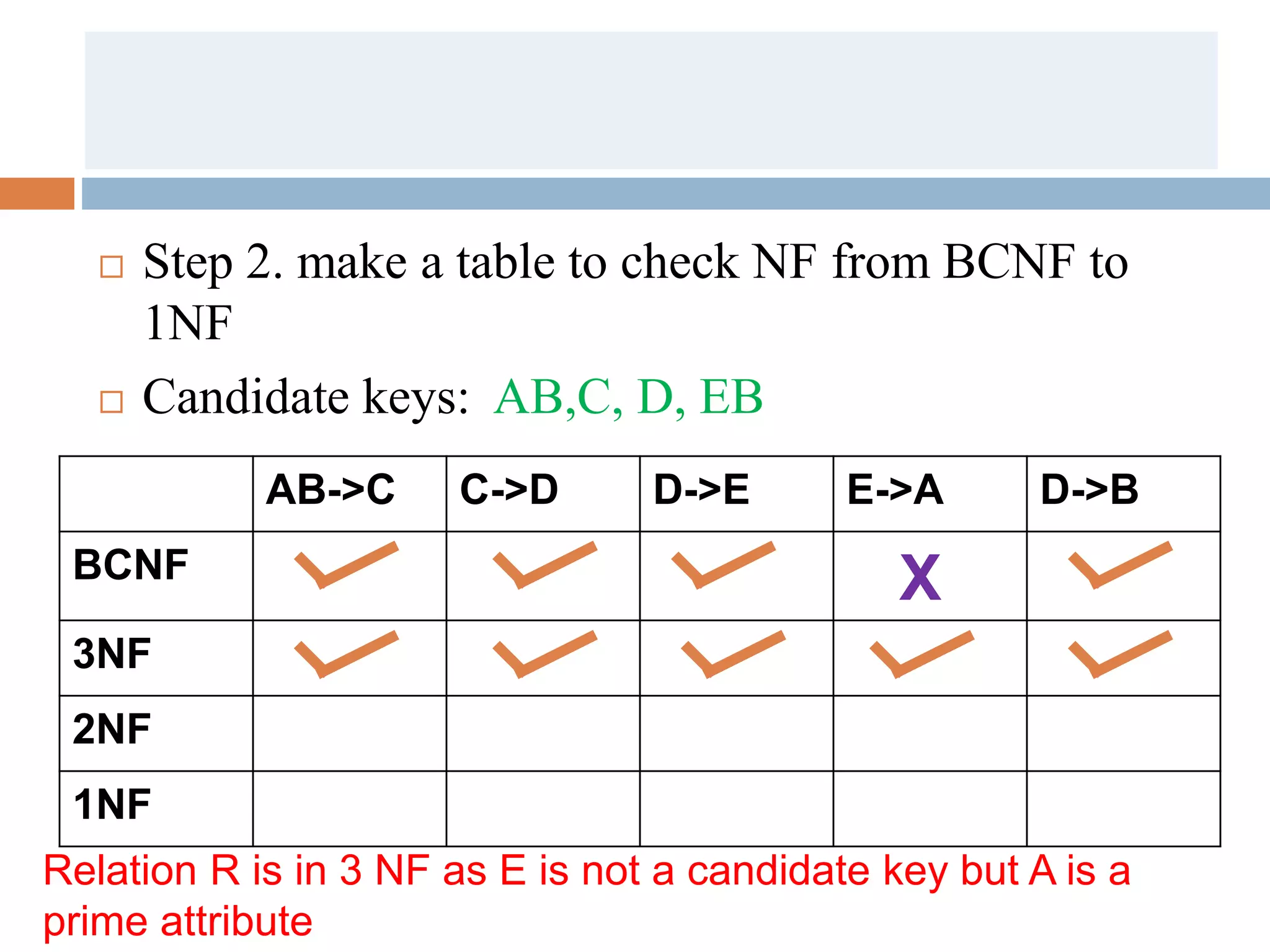
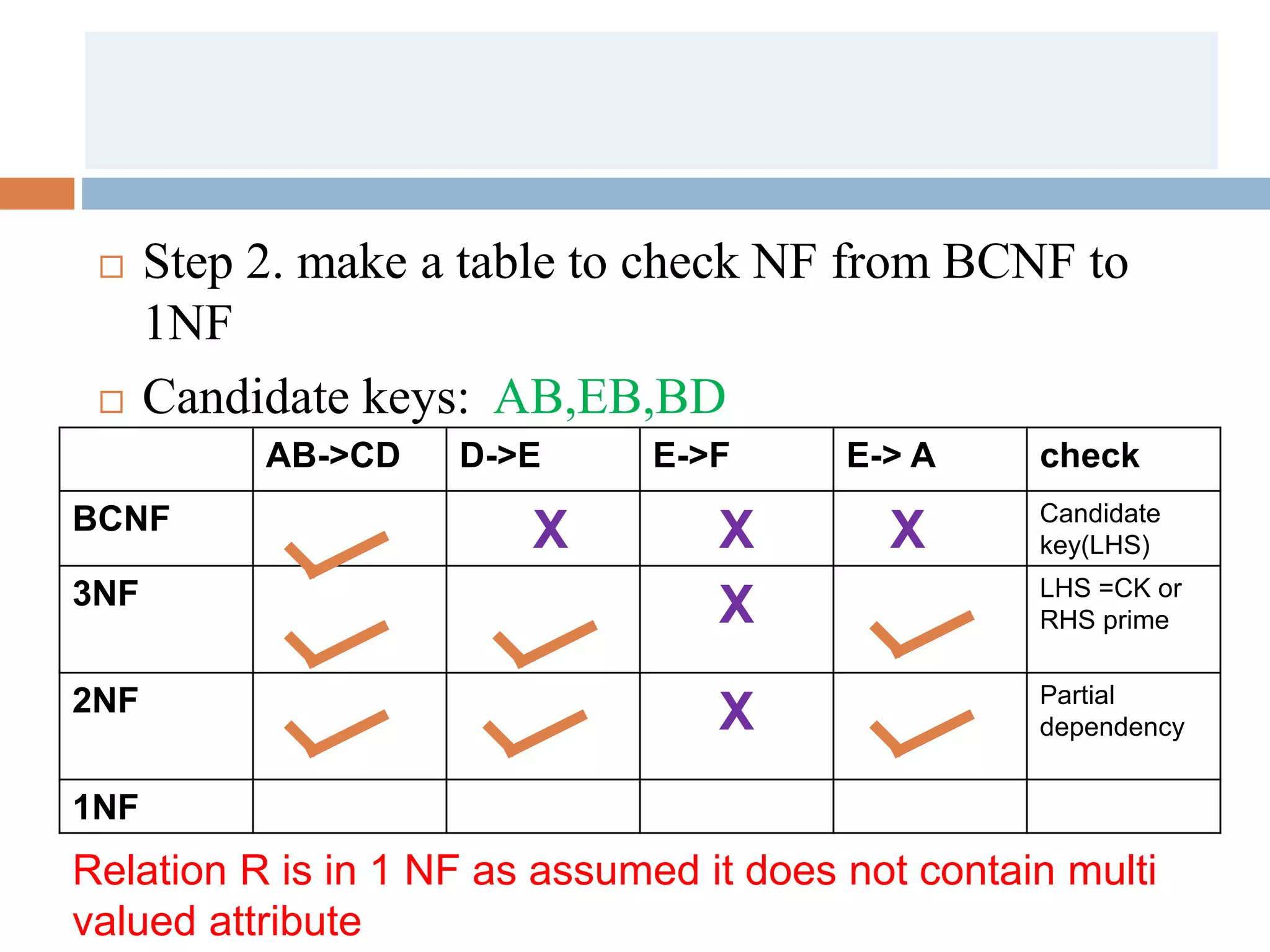
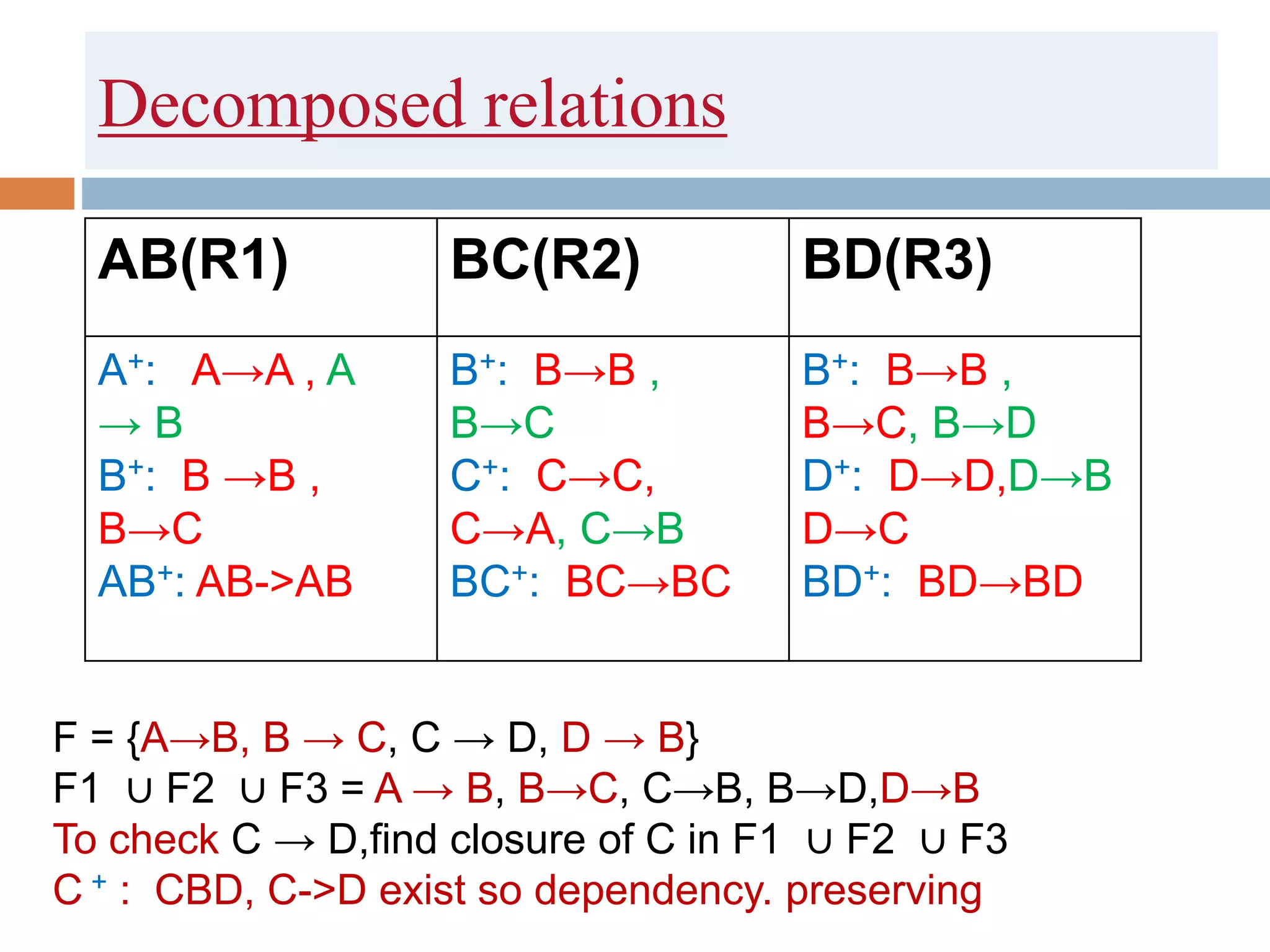
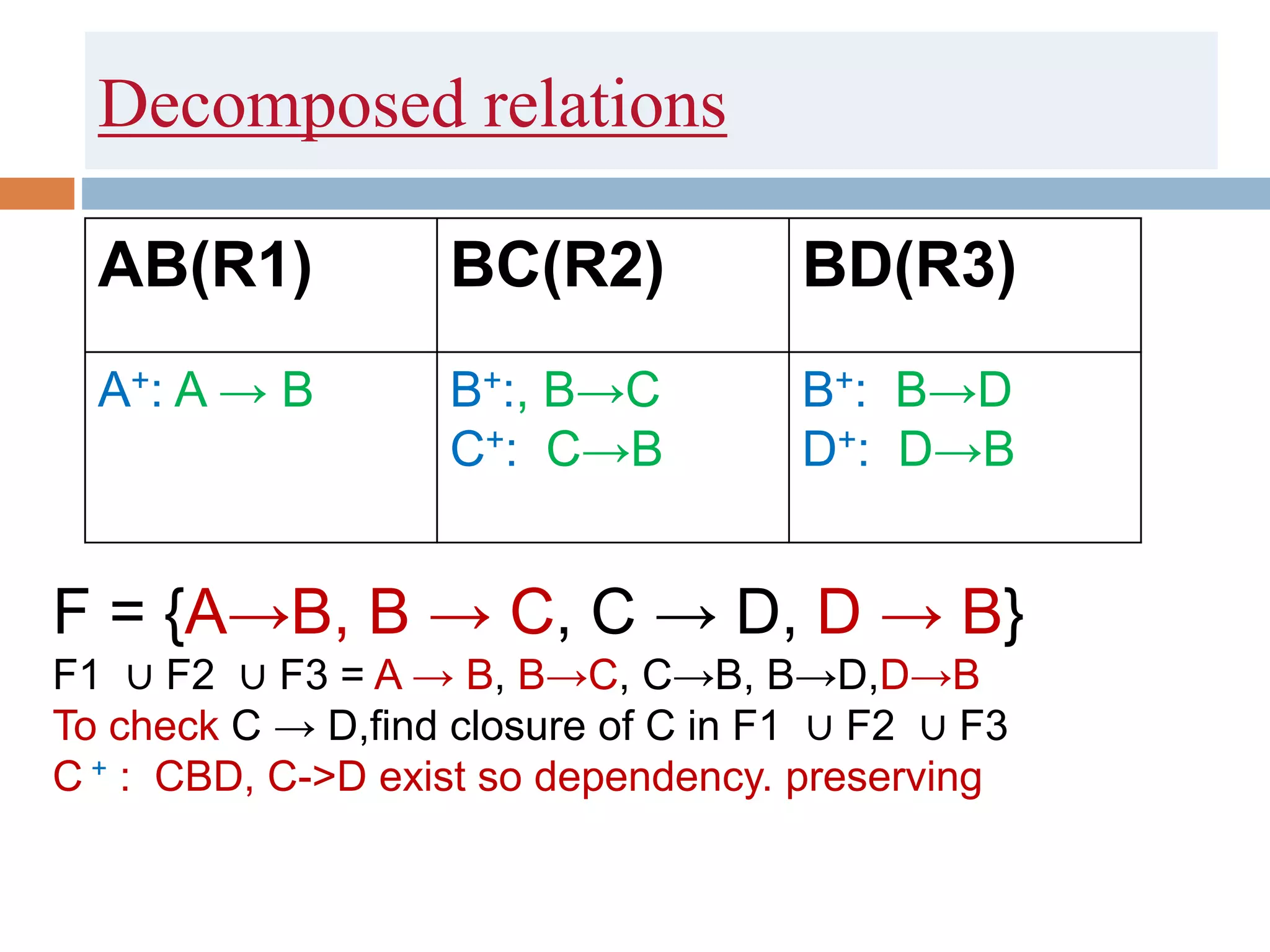
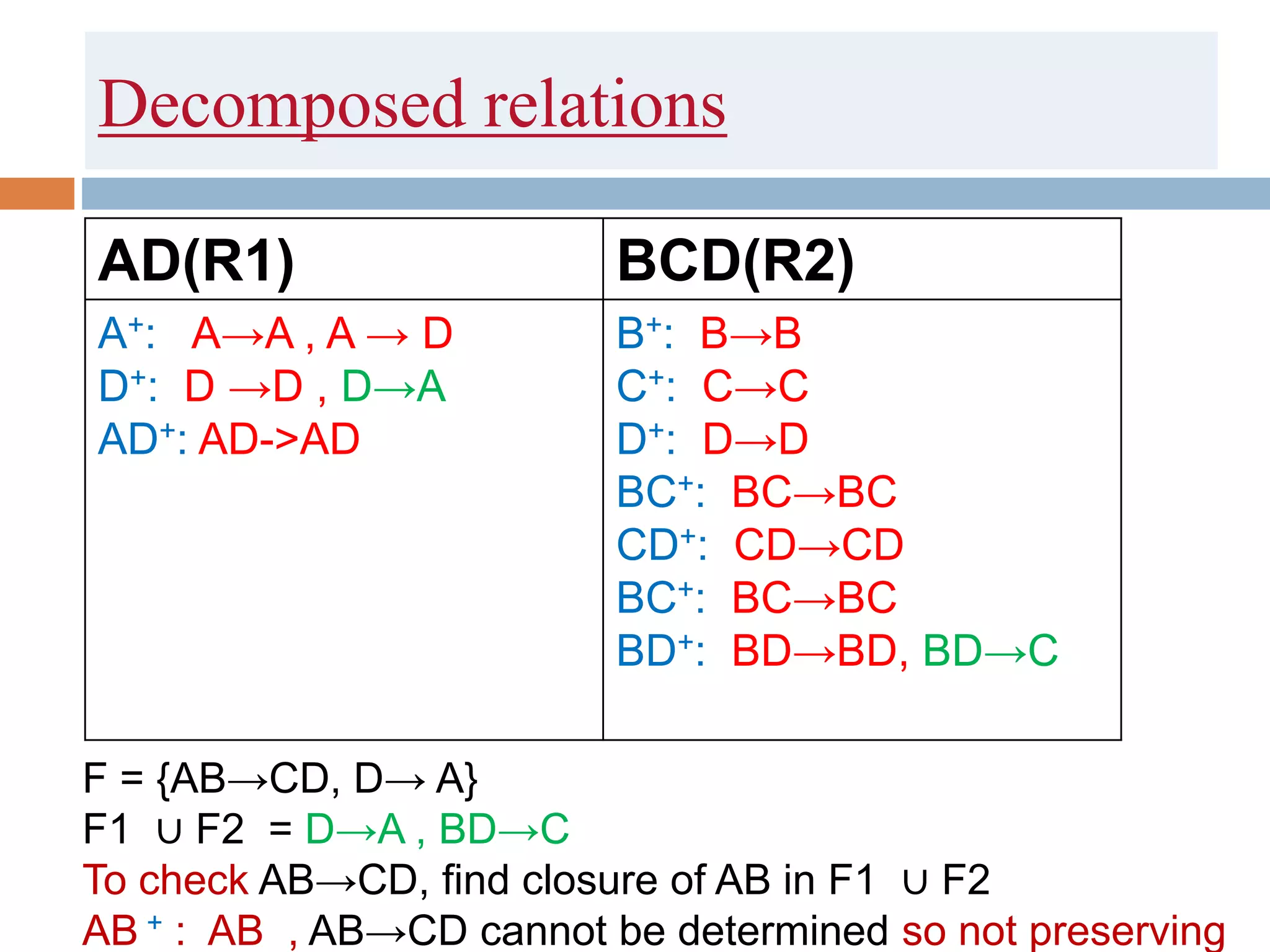
The document discusses database normalization and related concepts. It defines functional dependencies and different normal forms including 1NF, 2NF, 3NF, BCNF. Anomalies like insertion, update and deletion anomalies are explained using an example. The concepts of primary key, candidate key, composite key and partial vs full dependencies are also covered. Different types of functional dependencies like trivial, non-trivial and transitive are defined. The process of normalization up to BCNF is summarized.

1. DATABASE
NORMALIZATION
-VARSHA KUMARI

2. Content : Database Normalization:
 Functional dependencies
 Anomalies in database (Insert Update, Delete)
 Introduction to Normal forms based on primary keys
 First Normal Form
 Second Normal Form
 Third Normal Form
 Boyce Codd Normal Form
 De-normalization
 Lossless and Lossy Joins
 dependency preserving decomposition

3. Functional Dependancy (FDs)
 A functional dependency (FD) is a relationship
between two attributes, typically between the PK
and other non-key attributes within a table.

4. Functional Dependancy
A B
S 1
T 2
U 3
V 4
t1 ->
t2 ->
Let A and B are subset
of a Relation R
t1 ->
If t1(A) = t2(A)
then t1(B) = t2(B)
Then Functional Dependancy A-> B holds true:

5. Functional Dependancy
A B
S 1
S 2
U 3
V 4
t1 ->
t2 ->
Let A and B are subset
of a Relation R
t1 ->
If t1(A) = t2(A)
then t1(B) ! = t2(B)
Then Functional Dependancy A-> B does not holds true:

6. Functional Dependancy
A B
S 1
S 1
U 1
V 1
t1 ->
t2 ->
Let A and B are subset
of a Relation R
t1 ->
If t1(A) = t2(A)
then t1(B) = t2(B)
Then Functional Dependancy A-> B holds true:

7.  If A is unique then A-> B always holds true
 If values in B are all same then also A-> B always
holds true
 Now A and B can be a set of attributes

8. Functional Dependancy
University
Roll
S_name
U1 A
U2 A
U3 B
U4 C
University
Roll ->
S_name
True
S_name -> University Roll
False

9. Functional Dependancy
University
Roll
S_name
U1 A
U2 A
U3 B
U4 C
University
Roll ->
S_name
True
S_name -> University Roll
False

10. to check the determined attribute
 Given R( A, B, C, D, E)
 F = {A -> BC, DE ->C, B ->D}
 {A -> BC, C->DE, B ->D}
 Does A determine all other attributes?
 A->BC
 A-> ABC
 As B-> D so A->ABCD
 As c-> DE so A-> ABCDE
 Here we cannot determine E from A so A is not a
candidate key

11.  Given R( A, B, C, D, E)
 F = {A -> BC, DE ->C, B ->D}
 Is BE a key for R?
 BE -> BE
 As B-> D so BE-> BED
 As DE -> C so BE -> BEDC
 Here we cannot determine A from BE so A is not a
candidate key

12.  Given R( A, B, C, D, E)
 F = {A -> BC, DE ->C, B ->D}
 Is AE a candidate or super key for R?
 AE->AE
 As A-> BC so AE->ABCE
 As B->D so AE->ABCDE
 Here we can determine all the attributes of relation
R so AE is a candidate key
 Is ADE a candidate or super key for R?
 ADE is a superkey as ADE ⊃ AE

13. Various Axioms Rules of functional
dependency
Rule 1 Reflexivity
If A is a set of attributes and B is a subset of A, then A holds B. {
A → B }
Rule 2 Augmentation
If A hold B and C is a set of attributes, then AC holds BC. {AC
→ BC}
It means that attribute in dependencies does not change the
basic dependencies.
Rule 3 Transitivity
If A holds B and B holds C, then A holds C.
If {A → B} and {B → C}, then {A → C}
A holds B {A → B} means that A functionally determines B.
A. Primary Rules

14. B. Secondary Rules
Rule 1 Union
If A holds B and A holds C, then A holds BC.
If{A → B} and {A → C}, then {A → BC}
Rule 2 Decomposition
If A holds BC and A holds B, then A holds C.
If{A → BC} and {A → B}, then {A → C}
Rule 3 Pseudo Transitivity
If A holds B and BC holds D, then AC holds D.
If{A → B} and {BC → D}, then {AC → D}

15. Closure of Functional Dependencies
 Closure set F -> F+
 The set of all FDs that can be inferred from F
 We denote the closure of F by F+
 F+ is a superset of F

16.  Assume relation R (A, B, C)
 Given FDs : A → B, B → C, C → A
 What are the possible keys for R ?
 Step 1: find the closure of A , B, C
 A+ = AB =ABC
 B+ = BC =ABC
 C+ = CA =CAB
 Step 2: If X+ determines all the attributes then X
is a candidate key
 So all A, B and C are candidate keys for relation R.

17.  Assume relation R (A, B, C,D)
 Given FDs : A → B, B → D, C → A
 What are the possible keys for R ?
 A+ = ABD
 B+ = BD
 C+ = CABD
 D+ = D

18. Anomalies
 There are three types of anomalies that occur when
the database is not normalized. These are –
Insertion, update and deletion anomaly. Let’s take
an example to understand this.

19. S_I
D
S_nam
e
C_I
d
C_nam
e
F_i
d
F_nam
e
Salar
y
S1 A C1 C F1 T 5K
S2 B C1 C F1 T 5K
S3 A C2 C++ F2 T 10K
S4 B C1 C F1 T 5K
C3 Java F3 S 8K

20. Anomalies
1. Updation Anomaly:
- if we want to update F1 salary to 7 K , we need to
perform updation of all redundant copies.
2. Deletion Anomaly:
- if we want to delete s3 tuple then we are loosing
the information of f2.
3. Insert Anomaly:
-Not possible to insert F3 information without Sid.

21. To avoid redundancy we use
the concept of decomposition
Fid Fna
me
Cid Cna
me
Sala
ry
F1 T C1 C 5K
F2 T C2 C++ 10K
Sid Sna
me
Cid
S1 A C1
S2 B C1
S3 A C2
S4 B C1

22. Normalization
 Normalization is a set of rules to systematically
achieve a good design.
 If these rules are followed, then the DB design is
guarantee to avoid several problems:
 Inconsistent data
 Anomalies: insert, delete and update
 Redundancy:

23. Normalization
 Normalization is a process of organizing the data
in database to avoid data redundancy, insertion
anomaly, update anomaly & deletion anomaly.
 Here are the steps for normalization:
 First normal form(1NF)
 Second normal form(2NF)
 Third normal form(3NF)
 Boyce & Codd normal form (BCNF)
 Fourthnormal form(4NF)
 Fifth normal form(5NF)

24. Types of Functional Dependencies upto
BCNF
 Trivial functional dependency:
 Non-trivial functional dependency:
 Transitive dependency:

25. Trivial Functional dependency:
 The Trivial dependency is a set of attributes which
are called a trivial if the set of attributes are
included in that attribute.
 So, X -> Y is a trivial functional dependency if Y is
a subset of X.

26. Example:
Emp_id Emp_name
AS555 Harry
AS811 George
AS999 Kevin
Consider this table with two columns Emp_id and Emp_name.
{Emp_id, Emp_name} -> Emp_id is a trivial functional dependency as
Emp_id is a subset of {Emp_id,Emp_name}.

27. Non trivial functional dependency
 Functional dependency which also known as a
nontrivial dependency occurs when A->B holds
true where B is not a subset of A.
 In a relationship, if attribute B is not a subset of
attribute A, then it is considered as a non-trivial
dependency.

28. Example:
Company CEO Age
Microsoft Satya Nadella 51
Google Sundar Pichai 46
Apple Tim Cook 57
(Company} -> {CEO} (if we know the Company, we
knows the CEO name)
But CEO is not a subset of Company, and hence
it's non-trivial functional dependency.

29. Transitive dependency:
 A transitive is a type of functional dependency
which happens when t is indirectly formed by two
functional dependencies.
Company CEO Age
Microsoft Satya Nadella 51
Google Sundar Pichai 46
Alibaba Jack Ma 54

30.  Company} -> {CEO} (if we know the compay,
we know its CEO's name)
 {CEO } -> {Age} If we know the CEO, we know
the Age
 Therefore according to the rule of rule of
transitive dependency:
 { Company} -> {Age} should hold, that makes
sense because if we know the company name, we
can know his age.
Note:
You need to remember that transitive
dependency can only occur in a relation of three
or more attributes.

31. Normalization
 Normalization is a process of organizing the data
in database to avoid data redundancy, insertion
anomaly, update anomaly & deletion anomaly.
 Here are the steps for normalization:
 First normal form(1NF)
 Second normal form(2NF)
 Third normal form(3NF)
 Boyce & Codd normal form (BCNF)
 Fourthnormal form(4NF)
 Fifth normal form(5NF)
However (1NF, 2NF,
3NF) are sufficient for
normalization.

32. First normal form (1NF)
 Relation R is in 1NF only if
 an attribute (column) of a R does not contain multiple
values.
OR
 An attribute of R should hold only atomic values

33. Consider the student table
S_id S_name Course
S1 A C
S2 B C++/java
S3 C C++/python
Multi valued
attribute
Here , Relation student is not in 1NF as each attribute of a
table must have atomic (single) values and course attribute
does not satisfies.

34. Convert student into 1NF
S_id S_name Course
S1 A C
S2 B C++
S2 B java
S3 C C++
S3 C python
single
valued
attribute
Now , Relation student is in 1NF

35. Disadvantages
 Relation student still suffering from redundancy
problem.
 Find the functional dependancy from student table
?
 Sid->Sname T
 Sid,Course ->Sname T
 Sid,Sname-> course F
 Sname->Sid T

36. Second normal form (2NF)
 Relation R is in 2NF only if
 R is in 1NF (First normal form)
 No non-prime(non key) attribute is dependent on the
proper subset of any candidate key of table.
OR
 R should not contain any partial dependancy.
OR
 All non key attribute are fully dependant on candidate
key of the table.

37. Prime(key) and Non prime(Non key)
attributes
 Suppose Candidate key for relation R(A,B,C,D,E)
is AE
 Then prime attribute are : A, E
 Then Non-prime attribute are : B,C,D

38. Partial Dependancy
 Suppose Candidate key for relation R(A,B,C,D,E)
is AE
 If A-> C , here A is the subset of candidate key AE
and C is non prime attribute this is called partial
dependancy .
 If AE-> C , here AE is the candidate key and C is
non prime attribute this is called fully dependancy.

39. student in 1NF
S_id S_nam
e
Course
S1 A C
S2 B C++
S2 B java
S3 C C++
S3 C python
S_id -> S_name
S_id,Course ->
S_name
Here S_id,Course is
candidate key
Non key attribute =
S_name
And also
S_id -> S_name
So , Relation student is not in 2NF decompose the
relation

40. Convert student table into R1 and R2
S_id S_name
S1 A
S2 B
S3 C
S_id Course
S1 C
S2 C++
S2 java
S3 C++
S3 python
R1(Sid->Sname)
CK= Sid
R2(S_id,course->S_id,course)
CK = S_id,course
No partial dependency so R1 and R2 are in 2NF

41. Third Normal Form
 Relation R is in 3NF only if
 R is in 2NF (First normal form)
 Transitive functional dependency of non-prime
attribute on any super key should be removed.
OR
 R should not contain any transitive dependency.
OR
 For each non trivial functional dependency X->Y then
either X must be candidate key or super key or Y
must be prime attribute.

42. Transitive Dependency
 Let R be the relational schema with non trivial
functional dependency X->Y is transitive
dependency if
 1. X is not a candidate key
OR
 2. Y is non-prime attibute.
 Eg : Mob_no,name->name

43. Example of to check transitive
dependency.
 Relation R(A,B,C,D)
 And FD’s {A->B , B-> C, C-> D , D-> A}
 Here candidate keys are A,B,C,D
 So no transitive dependency.

44. Example to check 3NF
 Relation R(A,B,C,D) and FD’s ={AB->C, C->D}
 Here candidate key AB
 In AB->C, here AB is candidate key
 In C->D, here C is not a candidate key and D is
non prime attribute
 Here Transitive dependency exist so relation R is
not in 3NF

45. Solution: Decompose the relation
 R1(A,B,C) R2(C,D)
 FD’s={AB->C} FD’s={C->D}
 Ck=AB CK= C
 Now both relations are in 3NF.

46. Boyce & Codd normal form (BCNF)
 Relation R is in BCNF only if
 it is in 3NF
 and for every functional dependency X->Y,
X should be the candidate key or super key of the
table.
 It is an advance version of 3NF that’s why it is also
referred as 3.5NF. Also BCNF is stricter than 3NF.

47. Example to check BCNF
 Relation R(A,B,C,D) and FD’s ={AB->C, C->D}
 Here candidate key AB
 In AB->C, here AB is candidate key
 In C->D, here C is not a candidate key
 R is not in BCNF so decompose the relation

48. Solution: Decompose the relation
 R1(A,B,C) R2(C,D)
 FD’s={AB->C} FD’s={C->D}
 Ck=AB CK= C
 Now both relations R1 and R2 are in BCNF

49. Check the highest Normal Form
Example 1
 Consider a relation R(A,B,C,D,E)
 and FD’s ={AB->C, C->D, D->E, E->A, D->B}
 Step 1. Identify the Candidate key.
 Step 2. make a table to check NF from BCNF to 1NF

50. Check the highest Normal Form
 Consider a relation R(A,B,C,D,E)
 and FD’s ={AB->C, C->D, D->E, E->A, D->B}
 Step 1. Identify the Candidate key.
 Candidate keys: AB,C, D, EB
 AB+ = ABC=ABCD= ABCDE
 C+ = CD= CDE= CDEA=CDEAB
 D+ = DEB=DEBA = DEBAC
 E+ = EA , but EB+ = EAB= EABC= EABCD

51.  Step 2. make a table to check NF from BCNF to
1NF
 Candidate keys: AB,C, D, EB
AB->C C->D D->E E->A D->B
BCNF X
3NF
2NF
1NF
Relation R is in 3 NF as E is not a candidate key but A is a
prime attribute

52. Check the highest Normal Form
Example 2
 Consider a relation R(A,B,C,D,E,F)
 and FD’s ={AB->CD, D->E, E->F, E->A}
 Step 1. Identify the Candidate key.
 Step 2. make a table to check NF from BCNF to 1NF

53. Check the highest Normal Form
 Consider a relation R(A,B,C,D,E)
 and FD’s ={AB->CD, D->E, E->F, E->A}
 Step 1. Identify the Candidate key.
 Candidate keys: AB,EB,BD
 AB+ = ABCD= ABCDEF
 D+ = DE=DEFA , but BD+ = BDEFAC
 E+ = EFA , but EB+ = EFAB= EFABCD

54.  Step 2. make a table to check NF from BCNF to
1NF
 Candidate keys: AB,EB,BD
AB->CD D->E E->F E-> A check
BCNF X X X Candidate
key(LHS)
3NF X LHS =CK or
RHS prime
2NF X Partial
dependency
1NF
Relation R is in 1 NF as assumed it does not contain multi
valued attribute

55. Question
 Find the highest normal form of a
relation R(A,B,C,D,E) with FD set as {BC->D,
AC->BE, B->E}

56. Question
 Find the highest normal form of a
relation R(A,B,C,D,E) with FD set {A->D, B->A,
BC->D, AC->BE}

57. Question
 Find the highest normal form of a
relation R(A,B,C,D,E) with FD set {B->A, A->C,
BC->D, AC->BE}
 B+
 A+
 BC+
 AC+

58. Denormalization
 Normalization is the technique of dividing the data
into multiple tables to reduce the data redundancy
and inconsistency and to achieve data integrity.
 Denormalization increases redundancy as it is used
to combine multiple table data into one so that it
can be queried quickly.
 It is an optimization technique in which we add
redundant data to one or more tables.

59. Desirable Properties of Decomposition
 if we combine the decomposed table (de-
normalization), it should give the original table int
terms of rows and columns.
 the following two properties are described as:
 Lossless Join Decomposition Property
 Dependency Preserving Property

62. Lossless vs. Lossy Decomposition
 Consider relation R is divided into R1 and R2
 Lossless Decomposition
 R1 natural join R2 should create exactly R
 Lossy Decomposition
 R1 natural join R2 adds more records (or delete
records ) from R

65. To ensure lossless decomposition
 The common columns must be candidate key in
one of the two relations

66. Dependency preserving
 every dependency in original table must be
preserved or say, every dependency must be
satisfied by at least one decomposed table.

67. Dependency preserving
 Consider R be the original relational schema
having FD set F. Let R1 and R2 having FD set F1
and F2 respectively, are the decomposed sub-
relations of R.
 The decomposition of R is said to be preserving if
 F1 ∪ F2 ≡ F {Dependency Preserving}
 If F1 ∪ F2 ⊂ F {NOT Preserving Dependency}
 and F1 ∪ F2 ⊃ F {this is not possible}

68. Question 1
 Consider R(ABC) has following FD's
 F = {A→B, B → C, C → A}
 D = {AB,BC}
 check whether decomposition is dependency
preserving or not

69. Decomposed relations
AB(R1) BC(R2)
A+: A→A , A → B
B+: B →B , B→C,
B→A
AB+: AB->AB
B+: B→B , B→C
C+: C→C, C→A, C→B
BC+: BC→BC
F = {A→B, B → C, C → A}
F1 ∪ F2 ∪ F3 = A → B, B→A, B→C, C→B
To check C →A,find closure of C in F1 ∪ F2 ∪ F3
C + : CBA, C->A exist so dependency. preserving

70. Decomposed relations
AB(R1) BC(R2)
A+: A → B
B+: B→A
B+: B→C
C+: C→B
F = {A→B, B → C, C → A}
F1 ∪ F2 = A → B, B→A, B→C, C→B
To check C →A,find closure of C in F1 ∪ F2
C + : CBA, C->A exist so dependency. preserving

71. Question 2
 Consider R(ABCD) has following FD's
 F = {A→B, B → C, C → D,D → B}
 D = {AB,BC,BD}
 check whether decomposition is dependency
preserving or not

72. Decomposed relations
AB(R1) BC(R2) BD(R3)
A+: A→A , A
→ B
B+: B →B ,
B→C
AB+: AB->AB
B+: B→B ,
B→C
C+: C→C,
C→A, C→B
BC+: BC→BC
B+: B→B ,
B→C, B→D
D+: D→D,D→B
D→C
BD+: BD→BD
F = {A→B, B → C, C → D, D → B}
F1 ∪ F2 ∪ F3 = A → B, B→C, C→B, B→D,D→B
To check C → D,find closure of C in F1 ∪ F2 ∪ F3
C + : CBD, C->D exist so dependency. preserving

73. Decomposed relations
AB(R1) BC(R2) BD(R3)
A+: A → B B+:, B→C
C+: C→B
B+: B→D
D+: D→B
F = {A→B, B → C, C → D, D → B}
F1 ∪ F2 ∪ F3 = A → B, B→C, C→B, B→D,D→B
To check C → D,find closure of C in F1 ∪ F2 ∪ F3
C + : CBD, C->D exist so dependency. preserving

74. Question 3
 Consider R(ABCD) has following FD's
 F = {AB→CD, D→ A}
 D = {AD,BCD}
 check whether decomposition is dependency
preserving or not

75. Decomposed relations
AD(R1) BCD(R2)
A+: A→A , A → D
D+: D →D , D→A
AD+: AD->AD
B+: B→B
C+: C→C
D+: D→D
BC+: BC→BC
CD+: CD→CD
BC+: BC→BC
BD+: BD→BD, BD→C
F = {AB→CD, D→ A}
F1 ∪ F2 = D→A , BD→C
To check AB→CD, find closure of AB in F1 ∪ F2
AB + : AB , AB→CD cannot be determined so not preserving