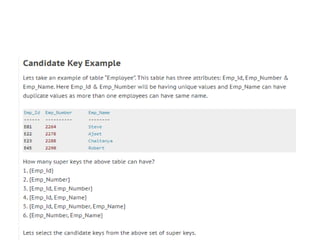
The document discusses functional dependencies and normalization forms. It defines functional dependency as a relationship between two attributes where the left side attribute determines the right side attribute. It provides an example of a functional dependency between Emp_Id and Emp_Name. It also defines trivial and non-trivial functional dependencies. The document then discusses candidate keys and how to find them. It provides examples and steps to find candidate keys and determine the total number of candidate keys and super keys. Finally, it discusses normalization forms up to fourth normal form (4NF), defining each form and providing examples.

2. Functional Dependency
• The functional dependency is a relationship that exists between
two attributes. It typically exists between the primary key and non-
key attribute within a table.
X → Y
• The left side of FD is known as a determinant, the right side of the
production is known as a dependent. Assume we have an employee
table with attributes: Emp_Id, Emp_Name, Emp_Address.
• Here Emp_Id attribute can uniquely identify the Emp_Name
attribute of employee table because if we know the Emp_Id, we can
tell that employee name associated with it.
Functional dependency can be written as:
Emp_Id → Emp_Name
We can say that Emp_Name is functionally dependent on Emp_Id.

3. Types of Functional dependency

4. • 1. Trivial functional dependency
A → B has trivial functional dependency if B is a subset of A.
The following dependencies are also trivial like: A → A, B → B
Consider a table with two columns Employee_Id and Emplo
yee_Name.
• {Employee_id, Employee_Name} → Employee_Id is a triv
ial functional dependency as
• Employee_Id is a subset of {Employee_Id, Employee_Name
}.
• Also, Employee_Id → Employee_Id and Employee_Name
→ Employee_Name are trivial dependencies too.

5. • Non-trivial functional dependency
• A → B has a non-trivial functional dependency
if B is not a subset of A.
• When A intersection B is NULL, then A → B is
called as complete non-trivial.
ID → Name,
Name → DOB

6. Candidate key
A candidate key may be defined as-
A set of minimal attribute(s) that can identify each
tuple uniquely in the given relation is called as a
candidate key.
OR
A minimal super key is called as a candidate key.
For any given relation, It is possible to have
multiple candidate keys.
• There exists no general formula to find the total
number of candidate keys of a given relation.

7. Example-
Consider the following Student schema-
Student ( roll , name , sex , age , address , class , section )
Given below are the examples of candidate keys-
( class , section , roll )
( name , address )
• These are candidate keys because each set consists of
minimal attributes required to identify each student
uniquely in the Student table.

8. Finding Candidate Keys
Step-01:
• Determine all essential attributes of the given
relation.
• Essential attributes are those attributes which are
not present on RHS of any functional
dependency.
• Essential attributes are always a part of every
candidate key.
• This is because they can not be determined by
other attributes.

12. PRACTICE PROBLEMS BASED ON
FINDING CANDIDATE KEYS-
Problem-01:
Let R = (A, B, C, D, E, F) be a relation scheme with the following
dependencies-
C → F
E → A
EC → D
A → B
Which of the following is a key for R?
CD
EC
AE
AC
Also, determine the total number of candidate keys and super keys.

13. Solution-
We will find candidate keys of the given relation in the
following steps-
Step-01:
Determine all essential attributes of the given relation.
Essential attributes of the relation are- C and E.
So, attributes C and E will definitely be a part of every
candidate key.

14. Step-02:
Now, We will check if the essential attributes together can determine all remaining
non-essential attributes.
To check, we find the closure of CE.
So, we have-
{ CE }+
= { C , E }
= { C , E , F } ( Using C → F )
= { A , C , E , F } ( Using E → A )
= { A , C , D , E , F } ( Using EC → D )
= { A , B , C , D , E , F } ( Using A → B )
We conclude that CE can determine all the attributes of the given relation.
So, CE is the only possible candidate key of the relation.
Thus, Option (B) is correct.

15. Total Number of Candidate Keys-
Only one candidate key CE is possible.
Total Number of Super Keys-
There are total 6 attributes in the given relation of which-
There are 2 essential attributes- C and E.
Remaining 4 attributes are non-essential attributes.
Essential attributes will be definitely present in every key.
Non-essential attributes may or may not be taken in every super key.
So, number of super keys possible = 2 x 2 x 2 x 2 = 16.
Thus, total number of super keys possible = 16.

16. Problem-02:
Let R = (A, B, C, D, E) be a relation scheme with
the following dependencies-
AB → C
C → D
B → E
Determine the total number of candidate keys
and super keys.

17. Solution-
We will find candidate keys of the given relation in the following steps-
Step-01:
Determine all essential attributes of the given relation.
Essential attributes of the relation are- A and B.
So, attributes A and B will definitely be a part of every candidate key.
Step-02:
Now,
We will check if the essential attributes together can determine all remaining non
essential attributes.
To check, we find the closure of AB.

18. So, we have-
{ AB }+
= { A , B }
= { A , B , C } ( Using AB → C )
= { A , B , C , D } ( Using C → D )
= { A , B , C , D , E } ( Using B → E )
We conclude that AB can determine all the attributes of the given relation.
Thus, AB is the only possible candidate key of the relation.
Total Number of Candidate Keys-
Only one candidate key AB is possible.
Total Number of Super Keys-
There are total 5 attributes in the given relation of which-
There are 2 essential attributes- A and B.
Remaining 3 attributes are non-essential attributes.
Essential attributes will be definitely present in every key.
Non-essential attributes may or may not be taken in every super key.
So, number of super keys possible = 2 x 2 x 2 = 8.
Thus, total number of super keys possible = 8.

19. Problem-03:
Consider the relation scheme R(E, F, G, H, I, J, K, L, M, N) and the set of functional
dependencies-
{ E, F } → { G }
{ F } → { I , J }
{ E, H } → { K, L }
{ K } → { M }
{ L } → { N }
What is the key for R?
{ E, F }
{ E, F, H }
{ E, F, H, K, L }
{ E }
Also, determine the total number of candidate keys and super keys.

20. Solution-
We will find candidate keys of the given relation in the following steps-
Step-01:
Determine all essential attributes of the given relation.
Essential attributes of the relation are- E, F and H.
So, attributes E, F and H will definitely be a part of every candidate key.
Step-02:
Now,
We will check if the essential attributes together can determine all remaining non-essential attributes.
To check, we find the closure of EFH.
So, we have-
{ EFH }+
= { E , F , H }
= { E , F , G , H } ( Using EF → G )
= { E , F , G , H , I , J } ( Using F → IJ )
= { E , F , G , H , I , J , K , L } ( Using EH → KL )
= { E , F , G , H , I , J , K , L , M } ( Using K → M )
= { E , F , G , H , I , J , K , L , M , N } ( Using L → N )
We conclude that EFH can determine all the attributes of the given relation.
So, EFH is the only possible candidate key of the relation.
Thus, Option (B) is correct.

21. Total Number of Candidate Keys-
Only one candidate key EFH is possible.
Total Number of Super Keys-
There are total 10 attributes in the given relation of which-
There are 3 essential attributes- E, F and H.
Remaining 7 attributes are non-essential attributes.
Essential attributes will be definitely present in every key.
Non-essential attributes may or may not be taken in every super key.
So, number of super keys possible = 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128.
Thus, total number of super keys possible = 128.

23. Normalization
Third Normal Form (3NF)
• A relation will be in 3NF if it is in 2NF and not contain any
transitive partial dependency.
• 3NF is used to reduce the data duplication. It is also used to
achieve the data integrity.
• If there is no transitive dependency for non-prime
attributes, then the relation must be in third normal form.
• A relation is in third normal form if it holds atleast one of
the following conditions for every non-trivial function
dependency X → Y.
X is a super key.
Y is a prime attribute, i.e., each element of Y is part of some
candidate key.

26. • Example 2 – Consider relation R(A, B, C, D, E)
A -> BC,
CD -> E,
B -> D,
E -> A
All possible candidate keys in above relation
are {A, E, CD, BC} All attribute are on right
sides of all functional dependencies are prime.

27. Boyce Codd normal form (BCNF)
• It is an advance version of 3NF that’s why it is
also referred as 3.5NF. BCNF is stricter than
3NF.
• A table complies with BCNF if it is in 3NF and
for every functional dependency
X->Y, X should be the super key of the table.

28. Example: Suppose there is a company wherein employees work in more than one department.
They store the data like this:

31. Fourth normal form (4NF)
• A relation will be in 4NF if it is in Boyce Codd
normal form and has no multi-valued
dependency.
• For a dependency A → B, if for a single value
of A, multiple values of B exists, then the
relation will be a multi-valued dependency.