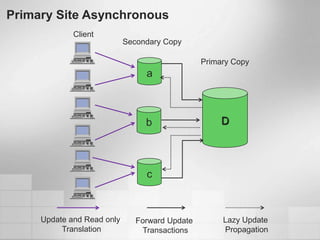
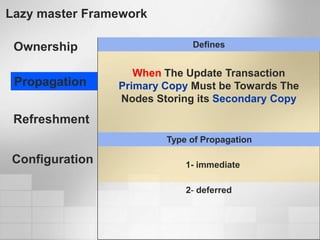
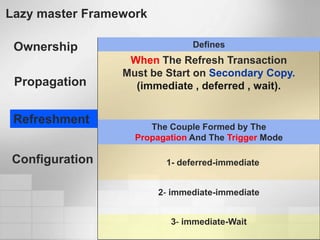
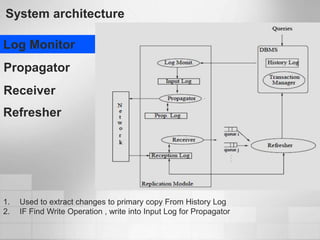
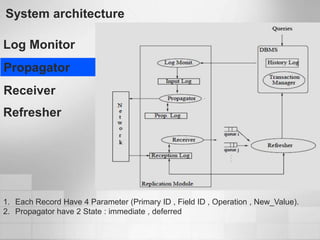
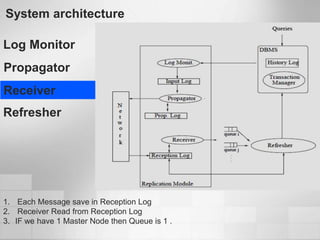
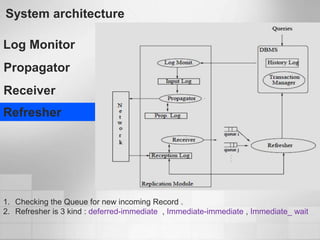
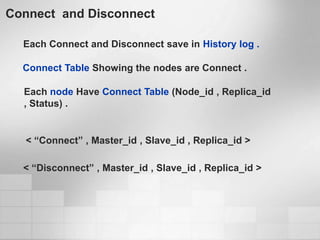
1. Software metrics are used to quantify attributes of software objects by mapping symbols to those objects. There are different types of metrics that can be calculated. 2. Important metrics include McCabe's cyclomatic complexity metric, which measures the number of linearly independent paths through a program, and Halstead's software science metrics which measure properties like program volume and difficulty. 3. Product metrics measure attributes of the software independent of how it was produced, like lines of code. Process metrics measure attributes relating to the development process.

1. Software MetricsEhsan hessamiIslamic Azad University OF Qazvin

2. What ?Software measurement is the mapping of symbols to objects

3. What ?Software measurement is the mapping of symbols to objectsWhy ?!!!!!!quantify some attribute of the objects

4. Criteria

5. CriteriaA metric must allow differententitiesto be distinguished.A metric must obey a representationcondition

6. Criteria…Each unit of the attribute must contribute an equivalent amount to the metricDifferent entities can have thesameattributevalue

7. Many timesthe attribute of interest is notdirectly measurable . An indirect measure involves ameasure and a predictionformula

8. Exampledensitymassvolume

9. Software Measurement Theory2 Kinds :numerical relation systemempirical relation system

10. The empirical relation systemtwo parts:A set of entities, EA set of relationships, R

11. The numerical relation systemtwo parts:A set of entities, NEXP : Integers , RealA set of relationships, PEXP : Less , Equal

12. MappingM, maps (E, R) to (N, P)related in the empirical systemrelated in the numberical system

13. MappingM, maps (E, R) to (N, P)related in the empirical systemrelated in the numberical systemEXP : x rel y if M(x) rel M(y)

14. EXP . Mappingmeasure, BIGX height=< Y height and X weight =< Y weight

15. MONOTONICITYIF increase the value of attribute , the object Will not Reverse.

16. MONOTONICITYIF increase the value of attribute , The object will not Reverse. Exp : 2y = XMonotonicityX>0 And X<52y = 5x - xIncreaesX>=5 And X<10DecreaseNot Monotonicity

17. MEASUREMENT SCALESThere are five different scale types :nominalordinalintervalratioabsolute

18. NormalThis type basically assigns numbers or symbols without regard to any quantity

19. NormalThis type basically assigns numbers or symbols without regard to any quantityEXP:

20. Ordinalthere is an implied ordering of the entities by the numbers assigned to the entity

21. Ordinalthere is an implied ordering of the entities by the numbers assigned to the entityEXP: First – SecondNot Equal1Second - third23

22. Intervalthe amount of the difference is constant

23. Intervalthe amount of the difference is constantEXP: converting from a Celsius to a FahrenheitFormule : 9.5 x +32

24. Ratiothe amount of the difference is constant and Well Zero

25. absoluteThe absolute is a counting scale measureEXP:

26. Product MetricsProduct metrics are metrics thatcan be calculated from the document independent of how it was produced . The most basic metric for size is thelinesof code metric .

27. McCABE’S CYCLOMATIC NUMBERintroduced in 1976 . Use the Gragh Theory : C = E – N + 2C = Cyclomatic number .E = number of Edges .N = number of Eodes .

28. McCABE’S CYCLOMATIC NUMBEREXP : 51432E = 11 N = 8C = 11 – 8 + 2 C = 5

29. McCABE’S CYCLOMATIC NUMBERCalculating the cyclomatic number from control flow graphs is time-consuming . McCabe found a more directMethod of calculating his measure .

30. McCABE’S CYCLOMATIC NUMBERRestriction : IN source Code : 1 decision IF , For , While Case or multiple Branch 1 less decision

31. McCABE’S CYCLOMATIC NUMBERRestriction … : Control flow graphs are required to have a distinct starting node and a distinct stoppingnodeFormula : C = D + 1D = Sum of Decisions

32. ExampleE = 2D = 1E = 2D = 1E = 3D = 2D = 4 C = 5Complexity

33. Threshold ValueIf the Complexity is greater than 10, efforts should be made to reduce the value or to split the module

34. HALSTEAD’S SOFTWARE SCIENCEHe did his work in the late 1960s and 1970s.He empirically looked for measuresof intrinsic size

35. HALSTEAD’S SOFTWARE SCIENCEvariablesOperandsconstantscommasparenthesesOperatorarithmetic operatorsbrackets

36. Basic Measures—η1 and η2η = η1 + η2 η =total count of unique tokensCount of unique Operatorη1 =Count of unique Operands η2 =

37. Basic Measures—η1 and η2Exp :z = 0;While x> 0 z = z + y ; x = x + 1;End –while ;Print(z) ;Operator = ; > + - Print () While-endwhileOperand z x y 0 1η1 =8 η2 = 5 η = 13

38. Length(N)N = N1 + N2 N =total count of tokensCount of OperatorN1 =Count of OperandsN2 =

39. LengthEXP : Operators= 3; 5While 1> 1+ 1- 1Print 1() 1OperandsZ 4X 3Y 20 21 1z = 0;While x> 0 z = z + y ; x = x + 1;End –while ;Print(z) ;N = N1 + N2 = 14+12 = 26

40. Estimate of the Length(est N)η1η2est N = η1*log + η2*log22

41. Estimate of the Length(est N)η1η2est N = η1*log + η2*log22Exp :η1=8 , η2=5est N = 8*3 +5*2.32 = 35.6

42. Volume ( V )Volume = number of bits(η1+ η2)V = N * Log2

43. Volume ( V )Volume = number of bits(η1+ η2)V = N * Log2Exp: N = 26 , η1=8 , η2=513V = 26 * Log = 96.22

44. Potential Volume, V*Potential Volume = Min number of bitsV* = (2 + η2*)log(2+ η2*)2η2* = The Minimal number of Operands

45. Other ParameterImplementation Level : L = V* / V

46. Other ParameterImplementation Level : L = V* / VEffort : E = V / L unit of Effors is emd

47. Other ParameterImplementation Level : L = V* / VEffort : E = V / L unit of Effors is emdTime :T = E / S18 emd / sec

48. HENRY–KAFURA INFORMATION FLOWmeasure the intermodule complexity of source code . HK = Weight *(out * in )iiiiIn = into the moduleiOut = out the module iWeight = weight the module i

49. HENRY–KAFURA INFORMATION FLOWExp : Weight = 1 HK = 1110