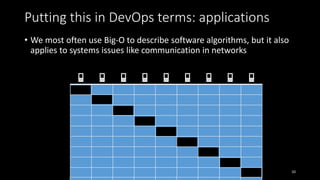
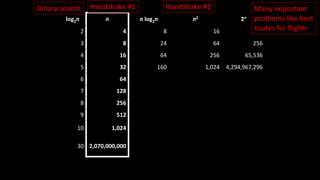
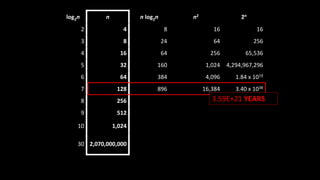
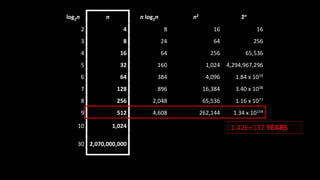
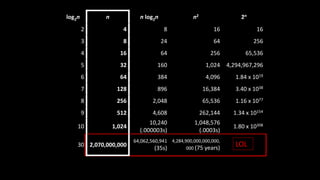
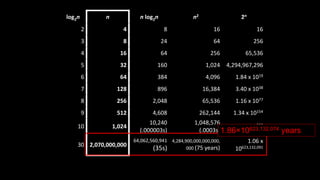
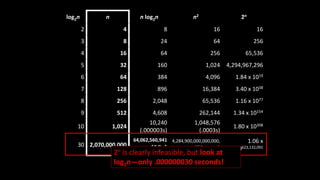
The document explains the concept of big-O notation, particularly in the context of DevOps and software performance. It illustrates how to analyze the time complexity of algorithms and systems, comparing linear (O(n)) and quadratic (O(n^2)) growth rates, alongside a binary search example demonstrating logarithmic performance (O(log n)). Additionally, it emphasizes the importance of understanding the structure of problems to effectively measure performance in network communications and systems.

2. ESSENTIAL BIG-O FOR DEVOPS

3. Before we start, let’s get introduced
3

4. Before we start, let’s get introduced
• Lets say I want to meet each of you today with a handshake and you tell me
your name…
• How many introductions need to happen?
There are N people in the room including me
But do I need to shake hands with myself, or tell myself my name?
N-1 introductions
4
🤵🤵
👩🤵
⚖️
💁♂️
👨🤵
🔬
👨
🎓
👳🤵
👩🤵
💻
👨🤵
🔧
Me
Me

5. Putting this in Big-O terms
• Big-O is a way of categorizing amount of work to be done in
general terms, with a focus on:
• Rate of growth as a function of the problem size N
• What that rate looks like on the horizon (i.e., for large N)
• Therefore, we don’t really care about an insignificant +/-1
5
🤵🤵
👩
🤵
⚖️
💁
♂️
👨
🤵
🔬
👨
🎓
💁
♂️
👨
🤵
🔬
👨
🎓
👳
🤵
👩
🤵
💻
👩
🤵
⚖️
💁
♂️
👨
🤵
🔬
👨
🎓
👳
🤵
👩
🤵
💻
👨
🤵
🔧
Me
Me

6. Putting this in Big-O terms
• For the first handshake problem, the rate N is important and the -1
constant is not, so N – 1 introductions becomes:
O( N )
• Similarly, if we said that each introduction takes 5 seconds, the
amount of work in terms of time is 3(N – 1) = 3N – 3, but we
disregard the constant 3s:
O( N )
6
-1
- 33

7. Before we start, let’s get introduced
• What if I not only want you to be introduced to me, but to each other?
• Now how many introductions?
7
🤵🤵
👩🤵
⚖️
💁♂️
👨🤵
🔬
👨
🎓
👳🤵
👩🤵
💻
👨🤵
🔧
Me
🤵🤵
👩🤵⚖️
💁♂️
👨🤵
🔬
👨🎓
👳🤵
👩🤵
N2

8. Before we start, let’s get introduced
• What if I not only want you to be introduced to me, but to each other?
• Now how many introductions?
8
N2(N - 1)2N2 - 2N + 1

9. Putting this in Big-O terms
• For the second handshake problem, the introductions was N2 - N:
O( N2 )
• But wait, didn’t we just say that a term of +/- N was important?
• For Big-O, we only care about the largest term of the polynomial
9
- 2N + 1

10. Putting this in DevOps terms: applications
• We most often use Big-O to describe software algorithms, but it also
applies to systems issues like communication in networks
10
🤵🤵
👩🤵
⚖️
💁♂️
👨🤵
🔬
👨
🎓
👳🤵
👩🤵
💻
👨🤵
🔧
Me
🤵🤵
👩🤵⚖️
💁♂️
👨🤵
🔬
👨🎓
👳🤵
👩🤵
📱 📱 📱 📱 📱 📱 📱 📱 📱
📱
📱
📱
📱
📱
📱
📱
📱
📱

11. 📱 📱 📱 📱 📱 📱 📱 📱 📱
📱
📱
📱
📱
📱
📱
📱
📱
📱
Putting this in DevOps terms: parallelism
• With all Big-O analysis, but especially when applying to networks and
systems, be careful about what you’re measuring!
• There are O(N2) communications, but they won’t take O(N2) time!
11

12. Putting this in DevOps terms: parallelism
• With all Big-O analysis, but especially when applying to networks and
systems, be careful about what you’re measuring!
• There are O(N2) communications, but they won’t take O(N2) time!
12
📱
📱
📱
📱
📱
📱
📱
📱
📱
📱

13. Search

14. Imagine storing sorted data in an array
• How long does it take us to find a number we
are looking for?
2 7 8 13 25 29 33 51 89 90 95

15. Imagine storing sorted data in an array
• How long does it take us to find a number we
are looking for?
• If you start at the front and proceed forward,
each inspection of an item rules out 1 item
O(N)inspections (worst case)
2 7 8 13 25 29 33 51 89 90 95

16. Imagine storing sorted data in an array
• If instead we jump right to the middle, one of
three things can happen:
1. The middle one happens to be the number we
were looking for, yay!
2. We realize we went too far
3. We realize we didn’t go far enough
2 7 8 13 25 29 33 51 89 90 95

17. Imagine storing sorted data in an array
• If instead we jump right to the middle, one of
three things can happen:
1. The middle one happens to be the number we
were looking for, yay!
2. We realize we went too far
3. We realize we didn’t go far enough
Ruling out HALF the options with one inspection
2 7 8 13 25 29 33 51 89 90 95

18. Binary search
• Let’s say the answer was case 3, “we didn’t go far
enough”:
• We ruled out the entire first half, and now only have the
second half to search
• We could start at the front of the second half and proceed
forward checking each item one at a time…
2 7 8 13 25 29 33 51 89 90 95

19. Binary search
• Let’s say the answer was case 3, “we didn’t go far
enough”
• We ruled out the entire first half, and now only have the
second half to search
• We could start at the front of the second half and proceed
forward checking each item one at a time… but why do
that when we know we have a better way?
• Jump right to the middle of the region to search
2 7 8 13 25 29 33 51 89 90 95

20. Binary search
• Let’s say the answer was case 3, “we didn’t go far
enough”
• We ruled out the entire first half, and now only have the
second half to search
• We could start at the front of the second half and proceed
forward checking each item one at a time… but why do
that when we know we have a better way?
• Jump right to the middle of the region to search
• Worst case cost is number of times we can divide
length in half: O(log2N)
2 7 8 13 25 29 33 51 89 90 95

21. Putting it all together

22. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64
7 128
8 256
9 512
10 1,024
30 2,070,000,000
Binary search Handshake #1 Handshake #2 Many important
problems like best
routes for flights

23. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64
7 128
8 256
9 512
10 1,024
30 2,070,000,000
2.4s
Easy!

24. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64 384 4,096 1.84 x 1019
7 128
8 256
9 512
10 1,024
30 2,070,000,000
194 YEARS

25. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64 384 4,096 1.84 x 1019
7 128 896 16,384 3.40 x 1038
8 256
9 512
10 1,024
30 2,070,000,000
3.59E+21 YEARS

26. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64 384 4,096 1.84 x 1019
7 128 896 16,384 3.40 x 1038
8 256
9 512
10 1,024
30 2,070,000,000
3,590,000,000,000,000,000,000
YEARS

27. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64 384 4,096 1.84 x 1019
7 128 896 16,384 3.40 x 1038
8 256 2,048 65,536 1.16 x 1077
9 512
10 1,024
30 2,070,000,000
For comparison: there are
about 10E+80 atoms in the
universe. No big deal.

28. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64 384 4,096 1.84 x 1019
7 128 896 16,384 3.40 x 1038
8 256 2,048 65,536 1.16 x 1077
9 512 4,608 262,144 1.34 x 10154
10 1,024
30 2,070,000,000
1.42E+137 YEARS

29. LOL
log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64 384 4,096 1.84 x 1019
7 128 896 16,384 3.40 x 1038
8 256 2,048 65,536 1.16 x 1077
9 512 4,608 262,144 1.34 x 10154
10 1,024
10,240
(.000003s)
1,048,576
(.0003s)
1.80 x 10308
30 2,070,000,000
64,062,560,941
(35s)
4,284,900,000,000,000,
000 (75 years)

30. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64 384 4,096 1.84 x 1019
7 128 896 16,384 3.40 x 1038
8 256 2,048 65,536 1.16 x 1077
9 512 4,608 262,144 1.34 x 10154
10 1,024
10,240
(.000003s)
1,048,576
(.0003s)
1.80 x 10308
30 2,070,000,000
64,062,560,941
(35s)
4,284,900,000,000,000,
000 (75 years)
1.06 x
10623,132,091
1.86×10623,132,074 years

31. log2n n n log2n n2 2n
2 4 8 16 16
3 8 24 64 256
4 16 64 256 65,536
5 32 160 1,024 4,294,967,296
6 64 384 4,096 1.84 x 1019
7 128 896 16,384 3.40 x 1038
8 256 2,048 65,536 1.16 x 1077
9 512 4,608 262,144 1.34 x 10154
10 1,024
10,240
(.000003s)
1,048,576
(.0003s)
1.80 x 10308
30 2,070,000,000
64,062,560,941
(35s)
4,284,900,000,000,000,
000 (75 years)
1.06 x
10623,132,091
2n is clearly infeasible, but look at
log2n—only .000000030 seconds!