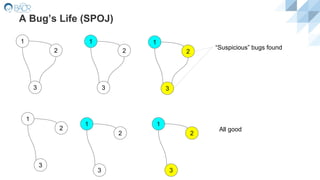
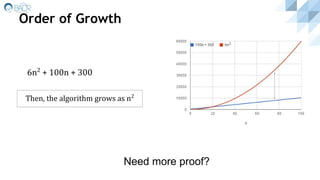
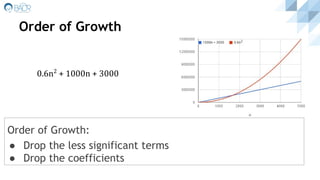
An algorithm is a set of steps to accomplish a task. Common algorithms include sorting, searching, and graph algorithms. Algorithms are described based on their correctness, resource usage, and asymptotic time complexity. Understanding algorithms helps improve coding skills and can aid career opportunities that involve algorithmic problem solving. Key algorithms were briefly outlined, including breadth-first search on graphs and using bipartite graph checks to verify assumptions about bug gender interactions.

2. Algorithms
A Sneak Peek

3. Definition
A broad definition: A set of steps to accomplish a task
● You use algorithms daily
○ Brush your teeth
○ Drive to work
○ ...
Replace the steps with code, and you get our algorithms

4. Ants (UVa)
Description
● n ants walk on L cm long pole. n and l are both known
● Speed of each ant is 1 cm/s
● When an ant reaches the end of the pole, it falls
● If two ants meet, they change direction. Otherwise,
they never change direction
● We know the original positions
● Assume that each ant can start in either direction
● Get the earliest time and latest time possible for all
ants to fall down
L

5. Ants (UVa)
Conflict
All ants are the same.
Color only means different
direction.
Change direction
Falls down

6. Ants (UVa)
● Earliest time for all to fall down?
● Just head to the nearest end
max(min(p0, L-p0), min(p1, L-p1), … min(pn-1, L-pn-1))
Answer

7. Ants (UVa)
● Latest time for all to fall down?
● Head to the farthest end
max(max(p0, L-p0), max(p1, L-p1), … max(pn-1, L-pn-1))
Answer

8. Ants (UVa)
● But what if two ants meet?
○ Each one should invert direction
● Should that matter?
Both invert direction Same length, same speed …
same time

9. How to Describe Algorithms
● Correctness
○ Some algorithms are expected to give one and exact correct
answer
■ Shortest driving route by GPS
○ Irrelevant from bad input
■ GPS not being fed by real-time data
○ We may tolerate a chance of error as long as we control it
■ Prime numbers test in RSA with Fermat Little Theorem
○ Nondeterministic
■ Even with the same input, the output can be different

10. How to Describe Algorithms
● Resource usage
○ Mainly CPU cycles, a.k.a time
■ Also, memory, network bandwidth, random bits, disk operations
○ How can we measure time performance for an algorithm?
■ e.g. If it takes t to solve n, then to solve an, it takes at?

11. Asymptotic notation
1. Measure time in terms of input
● Specifically, how many instructions per input size
2. Measure the rate of growth
● How fast it grows as input grows
● More: We’re interested in the dominant form (Order of
Growth)
t(n) = 25n + 500 25n dominates 500

12. Order of Growth
6n2
+ 100n + 300
Then, the algorithm grows as n2
Need more proof?

13. Order of Growth
0.6n2
+ 1000n + 3000
Order of Growth:
● Drop the less significant terms
● Drop the coefficients

14. Order of Growth - Different Notations
no
t(n) = Θ(n); then
k1
n < t(n) < k2
n; for all n > no
for some constants k1
, k2
and no
Big Theta

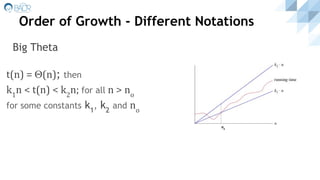
15. Order of Growth - Different Notations[4]
t(n) = O(f(n)); then
kf(n) < t(n); for all n > no
for some constants k and no
Big O
no
no
t(n) = Ω(f(n)); then
t(n) > kf(n); for all n > no
for some constants k and no
Big Omega

16. Order of Growth - Bubble Sort
func bubblesort( var a as array )
for i from 1 to N
for j from 0 to N - 1
if a[j] > a[j + 1]
swap( a[j], a[j + 1] )
end func
t(n) = 2 * (1 + 2 + … + (N - 1)) = 2 * (N * (N - 1) / 2)
t(n) = O(N2
)

17. Different Domains
● Sorting
● Binary search (Or searching generally)
● Graphs
● Strings
● Cryptography
● Data Compression
● Dynamic Programming
● Math
● Simulation
● Geography

18. Algorithms and You - Why You Should Care?
● It helps you become a better coder
● It’s not the complicated algorithms, it’s the skills
● Rarely would you encounter a problem that requires a
sophisticated algorithm
● Even in software giants

19. Algorithms and You - What Skills? [5]
● Fast coding, but careful coding
● Know the default language framework better
● Converting that mental model into something
● That’s what it’s all about
● Get in the code mode
● DEBUGGING
● ...

20. Algorithms and You - Why You Should Care?
● It would ease your way into the big companies and
more
● Interviews contain much more than algorithms, BTW…
● Some of the big companies host their own
competitions or watch closely on another
● Code Jam, Hacker Cup, ACM ICPC, Top Coder …
Managers! Please look away for a second!

21. Algorithms and You - Why You Should Care?
It’s fun and a great brain exercise.
Lastly,

22. Graphs - A Sneak Peek
● A graph is a set of vertices V and edges E
● An edge connects two vertices
● The edges can be directed or not
1
2
3
4
1
2
3
4

23. Graphs - A Sneak Peek
Everywhere in life
● Computers as vertices and wires as edges
● Road intersections and roads
● People as vertices and relationships as edges
● …

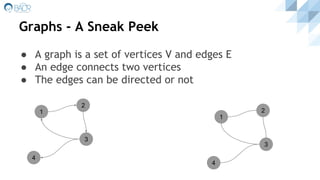
24. Graphs - A Sneak Peek
Representations
● Adjacency matrix
○ 2D boolean array, where matrix[i][j] = true, if there’s an
edge from node i to node j
● Adjacency list
○ Each node maintains a list, of all adjacent nodes
● Edge list
○ Store edges as pairs of nodes

25. Graphs - A Sneak Peek
Algorithms
● Searching
○ Breadth-first search, depth-first search
● Traversal
● Flood fill
● Shortest path
○ Dijkstra, Bellman-Ford, Floyd-Warshall
● Max-flow
● Bipartite graphs
● ...

26. Graphs - Sneak Peek
DFS using adjacency list
procedure DFS(G,v):
label v as discovered
for all edges w in G.adjacentEdges(v) do
if vertex w is not labeled as discovered then
recursively call DFS(G,w)
Complexity: O(n + m)

27. A Bug’s Life (SPOJ)
● Researching the sexual behaviour of a rare bug species
○ Note: Believe me. It’s a good problem! :D
● Assumingly, they have two genders
● We can identify all bugs by numbers, and we know all
interactions that happened
● Verify that the assumption is true.
○ i.e. There are no homsexual bugs

28. A Bug’s Life (SPOJ)
1
2
3
1
2
3
1
2
3
“Suspicious” bugs found
1
2
3
1
2
3
1
2
3
All good

29. A Bug’s Life (SPOJ)
Solution:
Bipartite graph check / Graph two-colors problem

30. A Bug’s Life (SPOJ)
hasSuspeciuosBugs(V):
for v in V:
if v is unmarked:
mark v with color1
if (visit(v))
return true
visit(v):
otherColor = //
for av in v.adjacencyList:
if av is marked:
if av.mark != otherColor:
return true
else:
av.mark = otherColor
if (visit(av))
return true
return false

31. References
1. Algorithms Unlocked by Thomas Cormen
2. Ants (UVa)
3. Nondeterministic Algorithms (WIkipedia)
4. Asymptotic Notation (Khan Academy)
5. Regarding the smug opposition to programming competitions
6. DFS (Wikipedia)
7. A Bug’s Life (SPOJ)
8. Bureaucracy (SPOJ)
9. Paradox (SPOJ)