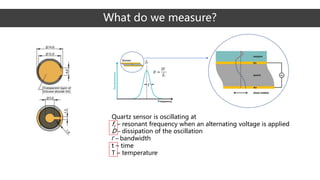
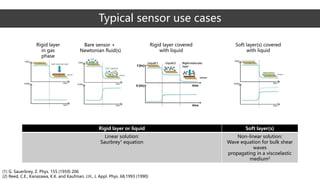
The document discusses QCM-D data analysis and architecture. It describes how data is collected from a quartz sensor oscillating under an alternating voltage. The data measures frequency and dissipation changes when rigid or soft layers are deposited on the sensor surface. The analysis aims to determine layer properties like thickness, shear modulus, and viscosity by fitting the data to theoretical models using a multi-step optimization process. The sensor can be used to study various biomolecular interactions and processes.

1. QCM-D Data Analysis
Architecture
by Gurbych Oleksandr,
Scientific Software Engineer at Biolin Scientific R&D

2. Where do the data
come from?

3. Where do the data
come from?

4. Quartz sensor is oscillating at
fr – resonant frequency when an alternating voltage is applied
D – dissipation of the oscillation
Г – bandwidth
t – time
T – temperature
What do we measure?

5. Rigid layer
in gas
phase
Bare sensor +
Newtonian fluid(s)
Rigid layer covered
with liquid
Soft layer(s) covered
with liquid
(1) G. Sauerbrey, Z. Phys. 155 (1959) 206
(2) Reed, C.E., Kanazawa, K.K. and Kaufman, J.H., J. Appl. Phys. 68,1993 (1990)
Rigid layer or liquid Soft layer(s)
Linear solution:
Saurbrey1 equation
Non-linear solution:
Wave equation for bulk shear
waves
propagating in a viscoelastic
medium2
Typical sensor use cases

6. What do we want to find?
Δ𝑓 ≈ −
𝑓0
ρ0ℎ0
· Δm ℎ =
Δ𝑚
𝜌
Δ𝑓 – frequency change, Hz
Δ𝑚 – mass change per unit area, g/cm2
h – layer thickness, nm
𝜌 – density of layer material
𝑓0, ρ0, ℎ0 - SiO2 crystal characteristics
Rigid layer - Sauerbrey equation: Soft layer – wave equation solutions3:
Δ𝑓 ≈ −
1
2π𝜌0ℎ0
𝜂3
𝛿3
+ ෍
𝑗=1,2
ℎ𝑗 𝜌𝑗ω − 2ℎ𝑗
𝜂3
𝛿3
2
𝜂 𝑗ω2
𝜇 𝑗
2
+ ω2 𝜂 𝑗
2
Δ𝐷 ≈ −
1
2π𝑓𝜌0ℎ0
𝜂3
𝛿3
+ ෍
𝑗=1,2
2ℎ𝑗
𝜂3
𝛿3
2
𝜇 𝑗ω
𝜇 𝑗
2
+ ω2 𝜂 𝑗
2 , 𝛿 =
2𝜂
𝜌ω
(3) Voinova M.V., Rodahl M. et.al. Viscoelastic Acoustic Response of Layered Polymer Films at Fluid-Solid Interfaces: Continuum Mechanics Approach. Physica Scripta.
Summary:
find Δm 𝜇 – shear modulus,
g/(m·s2)
𝜂 – viscosity, g/(m·s)
ω – angular frequency
Summary:
find ℎ1,2, 𝜇1,2,3, 𝜂1,2,3
(3 – 8 parameters optimization)

7. Very general scope
1 Time array
5-7 f arrays
5-7 D arrays
1 Temp array
~106 rows
~15 Mb
Calculation Engine*
+ select materials, liquids
+ set up measurements
+ set constraints (if needed)
* magic happens here

8. Smartfit 1: find local peaks

9. Smartfit 2: wide log-grid simplex search
fit parameter
fit parameter fit parameter
evaluation (LS)

10. Smartfit 3: backward narrow simplex search
fit parameter evaluation (LS)
fit parameter fit parameter

11. Smartfit 4: forward narrow simplex search
fit parameter evaluation (LS)
fit parameter fit parameter

12. Smartfit 5: linear interpolation & solutions selection
fit parameter evaluation (LS)
fit parameter fit parameter

13. General
Architecture

14. Data flow

15. Calculation Engine

16. Thank you!

17. 𝜇 + 𝑖ω𝜂 ·
∂2
𝑢 𝑥(𝑦, 𝑡)
∂𝑦2
= −ρω2
𝑢 𝑥(𝑦, 𝑡)
𝑢 𝑥 𝑦, 𝑡 = 𝐶1 𝑒−𝜉𝑦
+ 𝐶2 𝑒 𝜉𝑦
𝑒 𝑖ω𝑡
𝜉 =
1
𝛿
1 + 𝜒2 − 𝜒
1 + 𝜒2
+ 𝑖
1
𝛿
1 + 𝜒2 + 𝜒
1 + 𝜒2
𝜒 =
𝜇
𝜂ω
𝛿 =
2𝜂
𝜌ω
General solution:
where
where
and
𝜇 – shear modulus,
g/(m·s2)
𝜂 – viscosity, g/(m·s)
ω – angular frequency
Wave equation for bulk shear waves
propagating in a viscoelastic medium

18. Sensor Usage:
• Protein adsorbtion / desorbtionI
• Cell adhesionII
• Protein-protein interaction
• Degradation of polymers
• Biofouling and biofilm formation
• Drug analysisIII
• DNA / RNA BiosensorsIV
(I) Fredrik Hook, et. al., “Structural changes in hemoglobin during adsorption to solid surfaces: effects of pH, ionic strength and ligand binding”, Proc. Natl. Acad. Sci. US
(II) C. Fredriksson, S. Kihlman, M. Rodahl and B. Kasemo, “The Piezoelectric Quartz crystal Mass and Dissipation Sensor: A means of studyinng Cell adhesion”, Langmuir,
(III) Wei, W. Z. et. al. , “Selective pharmaceutical analyis technique with sensitive piezoelectric quartz sensors”, Anal. Lett. 26(11)(1993)2371.
(IV) Storri, S, Santoni, T., Mascini, M.,”A piezoelectric biosensor for DNA hybridization detection”, Anal. Lett. 31(11)(1998)1795.

19. Data flow (detailed)