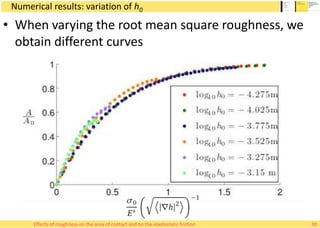
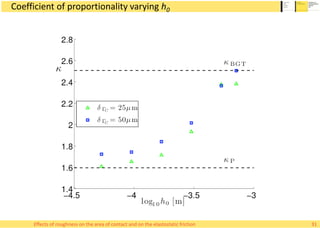
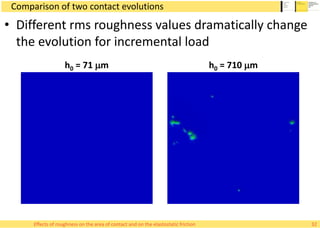
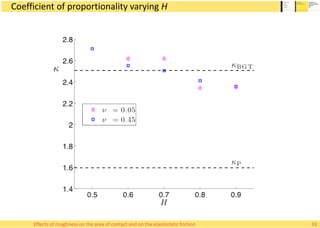
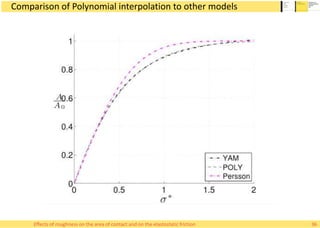
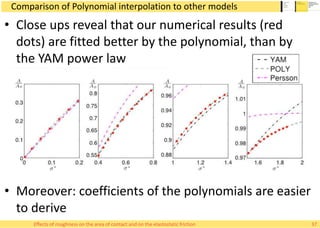
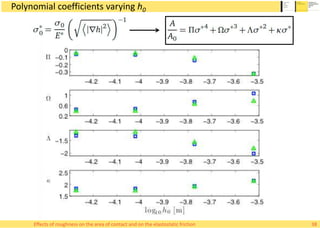
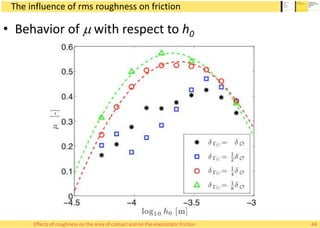
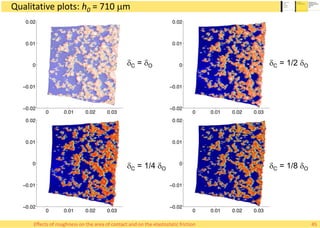
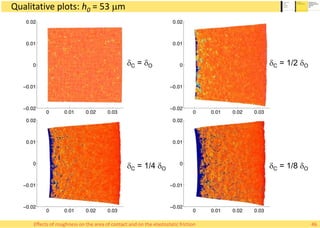
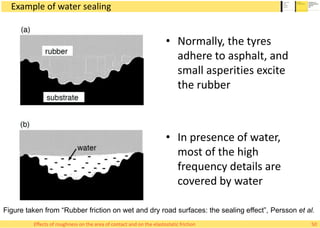
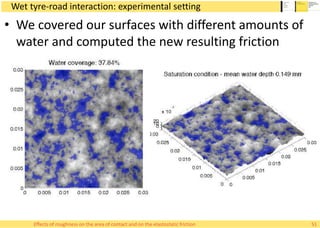
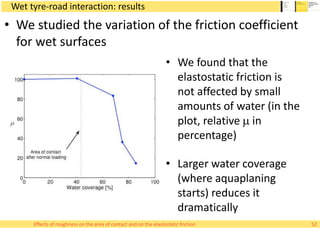
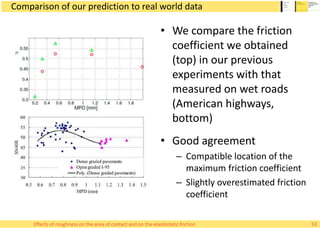
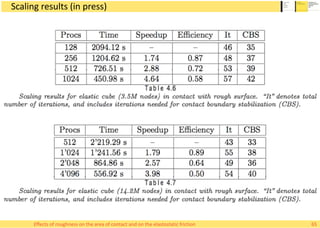
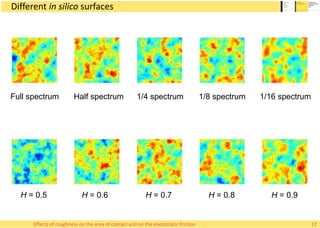
This document summarizes Alessandro Rigazzi's PhD dissertation defense on his research into modeling the effects of surface roughness on contact area and friction using finite element modeling. His research investigated how surface roughness parameters like root mean square roughness and Hurst exponent affect the real contact area between surfaces and elastic friction forces. Through numerical experiments on self-affine rough surfaces, he found that increasing roughness decreases contact area and increases friction coefficient in a way that can be modeled with polynomials. He also validated the models by simulating tire-road contact and comparing to experimental data on wet roads.








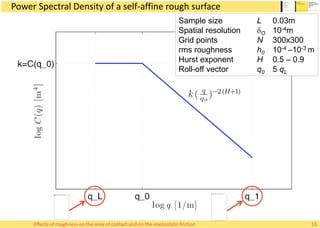
![Roughness
• We need to formally define roughness
• Many measures exist covering different aspects of
roughness
– Root mean square roughness
– Mean profile depth
– …
• But we prefer a compact description based on the
Power Spectral Density (PSD) of the surfaces
– Geometric measures can be derived [Nayak 1971]
Effects of roughness on the area of contact and on the elastostatic friction 9](https://image.slidesharecdn.com/169eca85-c8c6-44b3-a3f4-a87c4f3744ce-150818085352-lva1-app6892/85/rigazzi_phd_defense-9-320.jpg)










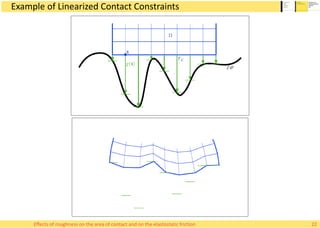
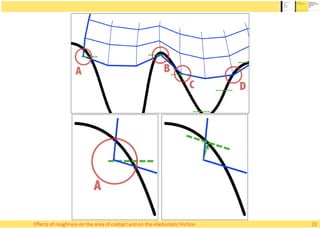


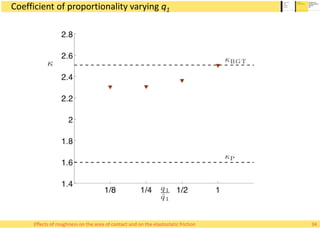
![Real area of contact, analytical models
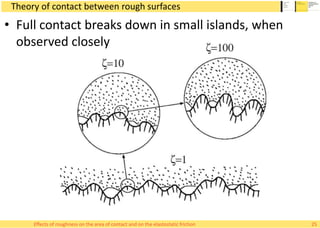
• There exist two prominent theoretical models
for the relation of load and real area of contact
– Bush-Gibson-Thomas (BGT) model [1975]
– Persson’s model [2000]
• BGT model considers the surface asperities as
acting separately on the elastic body
– No merging of contact islands
• Persson’s model assumes that the stress
diffuses over the contact area uniformly
– No isolation of contact clusters
27Effects of roughness on the area of contact and on the elastostatic friction](https://image.slidesharecdn.com/169eca85-c8c6-44b3-a3f4-a87c4f3744ce-150818085352-lva1-app6892/85/rigazzi_phd_defense-27-320.jpg)