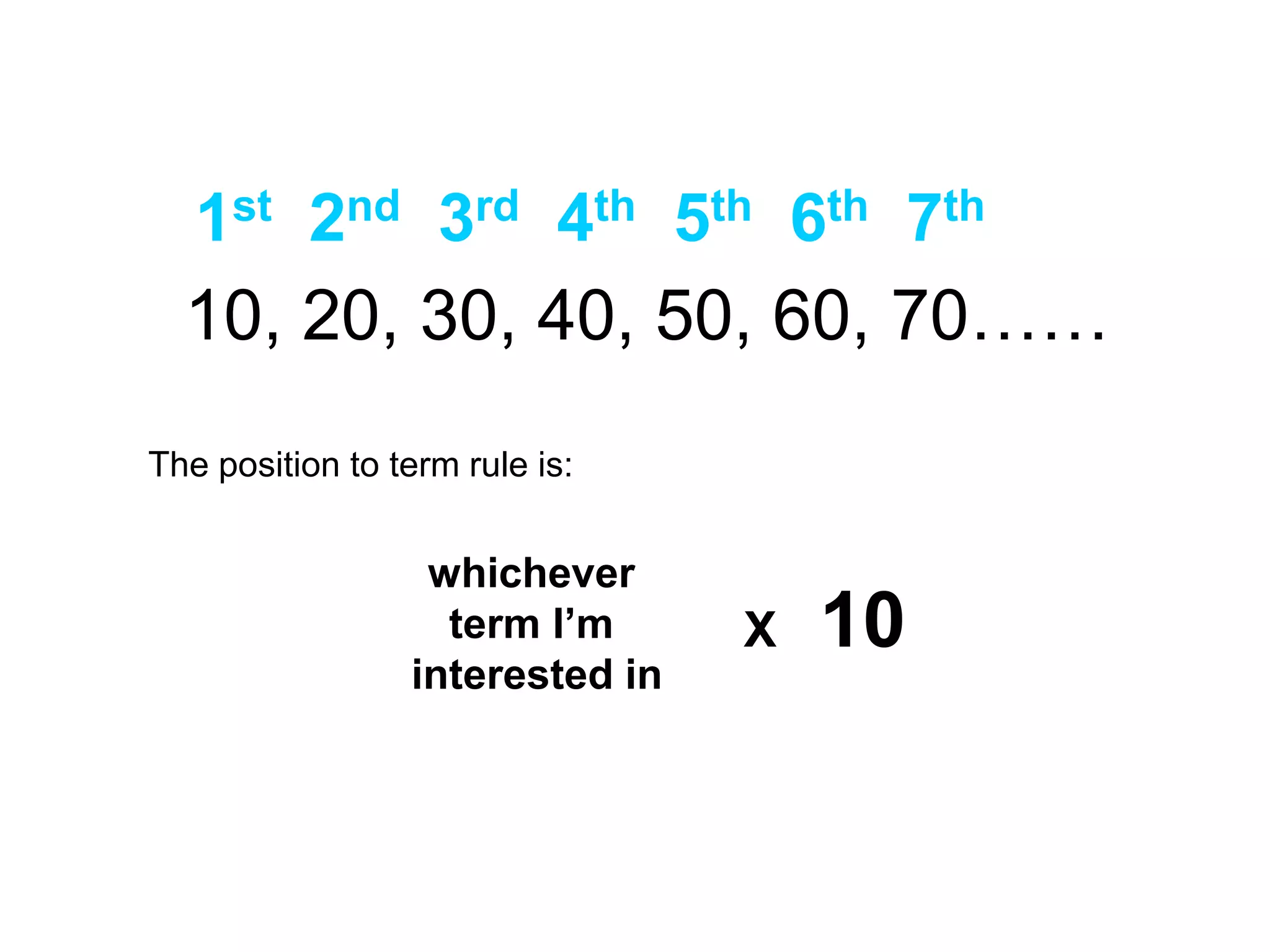
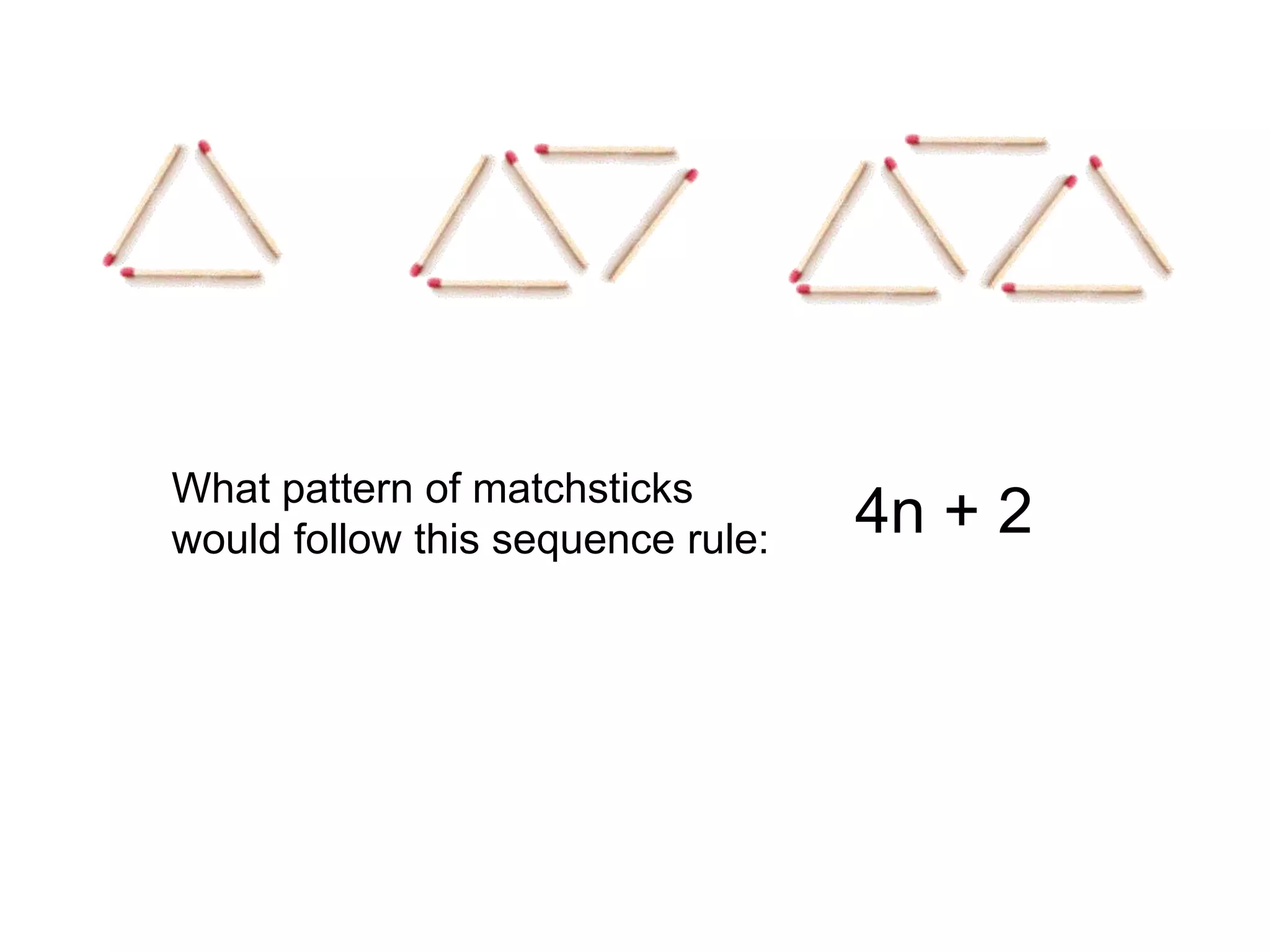
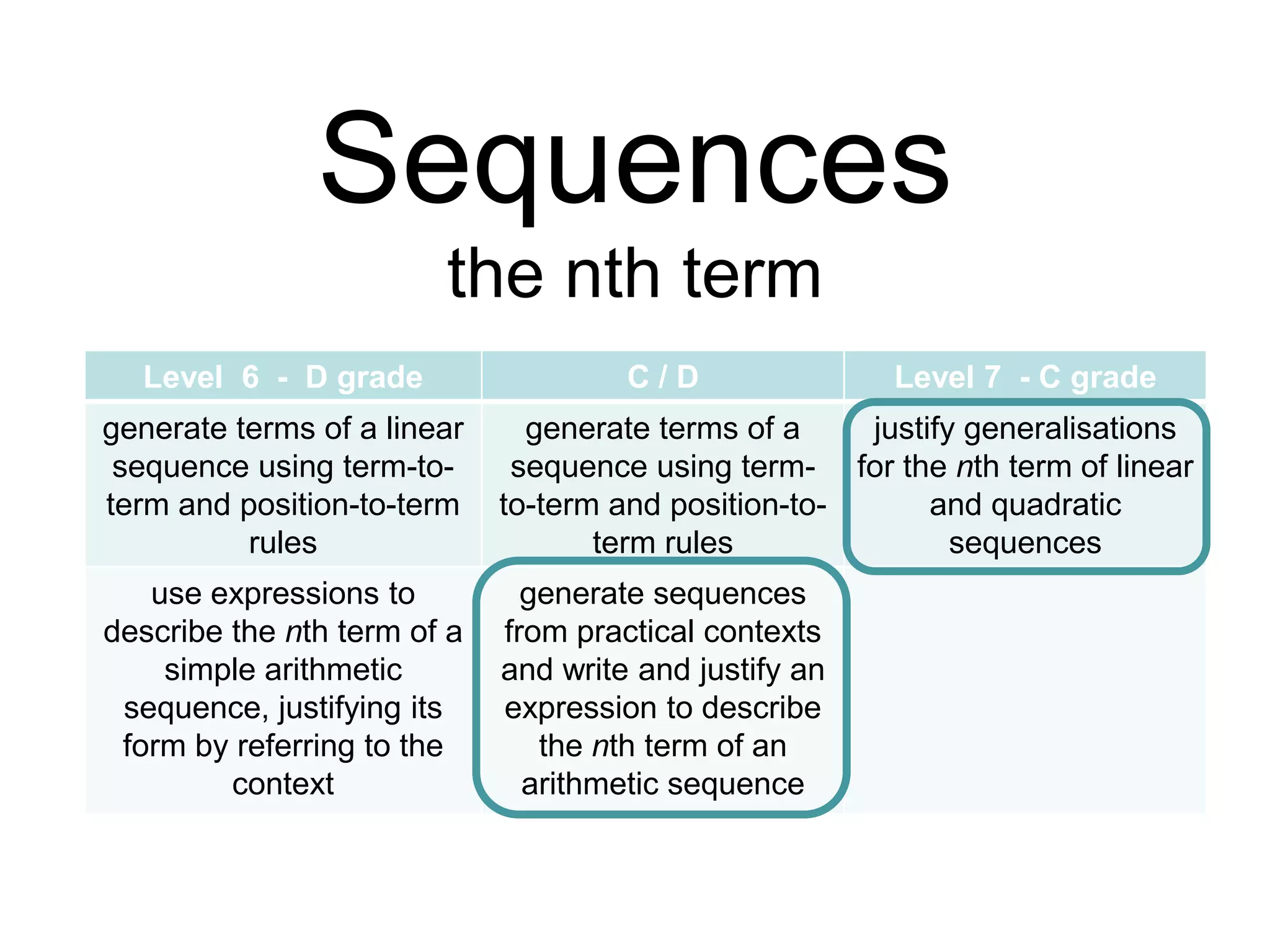
The document contains examples of arithmetic sequences and their term-to-term and position-to-term rules. It provides sequences and asks the reader to determine the rule for the nth term. It also includes word problems about taxi fares and matchstick patterns that can be represented by sequences. The document covers generating terms of sequences, justifying expressions for the nth term, and extending work to quadratic sequences.

1. A few sequences…
9, 13, 17, 21….
….. 25, 29
term to term rule: add 4

2. A few sequences…
20, 15, 10, 5….
….. 0, -5
term to term rule: minus 5

3. A few sequences…
1, 10, 100, 1000….
….. 10,000, 100,000
term to term rule: x 10

4. A few sequences…
88, 44, 22, 11….
….. 5.5, 2.75
term to term rule: half

5. Sequences
the nth term
Level 6 - D grade
generate terms of a linear
sequence using term-toterm and position-to-term
rules
write an expression for
the nth term of a simple
arithmetic sequence,
C/D
Level 7 - C grade
generate terms of a
justify generalisations
sequence using term- for the nth term of linear
to-term and position-toand quadratic
term rules
sequences
generate sequences
from practical contexts
and write and justify an
expression to describe
the nth term of an
arithmetic sequence

6. 1st 2nd 3rd 4th 5th 6th 7th
10, 20, 30, 40, 50, 60, 70……
The position to term rule is:
whichever
term I’m
interested in
X
10

7. 1st 2nd 3rd 4th 5th 6th 7th
4, 8, 12, 16, 20, 24, 28……
The position to term rule is:
n
whichever
term I’m
interested in
X
4
nth term = n x 4

8. What is the position to term rule:
2, 4, 6, 8, 10 ….
nth term = n x 2 = 2n
6, 12, 18, 24 ….
nth term = 6n
5, 10, 15, 20, 25….
nth term = 5n
100, 200, 300, 400….
nth term = 100n
What’s the 7th term?
700
What’s the 10th term?
1000
What’s the 18th term?
1,800

9. more complicated….
5, 8, 11, 14, 17, 20 …..
+3
1
2
3
4
+3
+3
+3
+3
common difference is 3
5
6
7
8
9
10 11 12 13 14 15 16 17
5
6
7
8
9
10 11 12 13 14 15 16 17
+2
1
2
3
4
nth term = 3n + 2

10. To work out the rule for the nth term of a sequence
6, 11, 16, 21, 26…
Step 1: Common difference?
Step 2: How has the table been shifted?
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17
7
8
9
10 11 12 13 14 15 16 17
+1
1
2
3
4
5
6
nth term = 5n + 1

11. Work out the rule for the nth term then work out the 100th term
a) 3, 5, 7, 9, 11, 13….
b) 12, 20, 28, 36, 44….
c) 19, 29, 39, 49, 59….
!! d) 7, 10, 13, 16, 19….
Extension:
h) 1, 9, 17, 25, 33….
i) -2, 8, 18, 28, 38….
e) 14, 20, 26, 32, 38….
f) 55, 60, 65, 70, 75…
!! g) 8, 17, 26, 35, 44….
j) -2, -4, -6, -8, -10…
k) 1, 4, 9, 16, 25….
l) 3, 6, 11, 18, 27….

12. You own a taxi company that charges as follows:
• £3.50 for calling the cab
• 20p for every minute of journey time
1. Work out a formula for the cost of a journey that’s n minutes long
2. Use your formula to cost a journey of 2 hours

13. What pattern of matchsticks
would follow this sequence rule:
4n + 2

14. Sequences
the nth term
Level 6 - D grade
C/D
Level 7 - C grade
generate terms of a linear
sequence using term-toterm and position-to-term
rules
generate terms of a
justify generalisations
sequence using term- for the nth term of linear
to-term and position-toand quadratic
term rules
sequences
use expressions to
describe the nth term of a
simple arithmetic
sequence, justifying its
form by referring to the
context
generate sequences
from practical contexts
and write and justify an
expression to describe
the nth term of an
arithmetic sequence

15. Extension work
T(n) = n2
T(n) = 3n2 + n
T(n) = 4n2 + n – 1
•
•
•
•
For each of these sequences work out the first five terms
What is the first difference?
What is the second difference?
Is there a way of predicting the second difference?