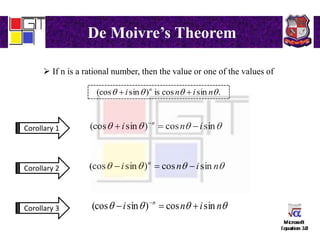
This document contains an assignment on complex numbers and functions for a BE Mechanical engineering course. It covers the following topics in 3 paragraphs or less each: 1) De Moivre's theorem and its corollaries for representing complex numbers as polar coordinates. Roots of a complex number using De Moivre's theorem. 2) Examples of using De Moivre's theorem to find all roots of complex numbers. 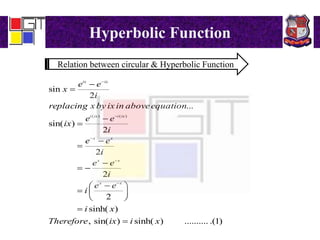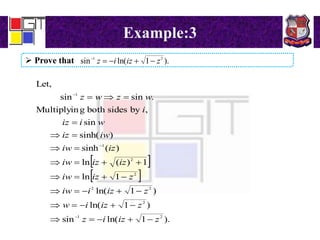3) Definitions of hyperbolic functions as extensions of circular functions to complex numbers. Relations between circular and hyperbolic functions and identities for hyperbolic functions. An example problem proving an identity for a hyperbolic function of a complex number.

1. GANDHINAGAR INSTITUTE OF
TECHONOLOGY(012)
SUBJECT : Complex Variables & Numerical Methods
(2141905)
Active Learning Assignment on the topic of
“Complex Numbers & Functions”
BE Mechanical Sem:4
Prepared By: Yash D. Pandya
Guided By : Prof. Mansi Vaishnani

2. OVERVIEW
 De Moivre’s Theorem
 Roots of a Complex Number
 Example
 Hyperbolic Function
 Reference

3. De Moivre’s Theorem
 If n is a rational number, then the value or one of the values of
.sincosis)sin(cos  nini n

Corollary 1
Corollary 2
Corollary 3
 sincos)sin(cos ini n
 
 nini n
sincos)sin(cos 
 nini n
sincos)sin(cos  

4. Roots of a Complex Number
 De Moivre’s therom is also useful for finding roots of a complex number.
 If n is any positive integer, then by De Moivre’s therom…


sincossincossincos i
n
ni
n
n
n
i
n
n



















 
    




sin2sinandcos2cos
function;trictrigonometheofnatureperiodicbyobtainedbemayrootsremainingThe
sincossincos
;sincosofrootntheofoneissincosThus,
1



kk
n
i
n
i
i
n
i
n
n
th

5. Roots of a Complex Number
General Form
      





 





 


n
k
i
n
k
kiki nn


2
sin
2
cos
2sin2cossincos
11
   
above.asorderinrootssamethegivek willofluesfurther vaThe
)1(2
sin
)1(2
cos,1
.........
.........
2
sin
2
cos,1
sincos,0
For
follows;As.1...,3,2,1forsincosofrootstheallgiveswhich
1



 



 






 





 



n
n
i
n
n
nk
n
i
n
k
n
i
n
k
nki n





6. Example:1
 Solve and find its all roots.014
z
 
.3,2,1,0;
4
12
sin
4
12
cos
)2sin()2cos(
)sin(cos
)1(
4
1
4
1
4
1











 





 




k
k
i
k
kik
i
z



)1(
2
1
22
1
4
7
sin
4
7
cos,3
)1(
2
1
22
1
4
5
sin
4
5
cos,2
)1(
2
1
22
1
4
3
sin
4
3
cos,1
)1(
2
1
22
1
4
sin
4
cos,0
For
4
3
2
1
i
i
izk
i
i
izk
i
i
izk
i
i
izk









7. Example:2
 Find all roots of .3
8i
iz
iz
iz
80
08
then,8Let
3
3
3



 We have = /2 and r = |z| = 8….therefore, 
.2,1,0;
6
14
sin
6
14
cos2
2
2sin
2
2cos8z
Hence,
2
2sin
2
2cos8
2
sin
2
cos8
)sin(cos
3
1
3
1
3











 





 















































k
k
i
k
kik
kik
i
irz












8. iiiizk
i
i
izk
i
i
izk
2)0(2
2
3
sin
2
3
cos2
6
9
sin
6
9
cos2,2For
3
22
3
2
6
5
sin
6
5
cos2,1For
3
22
3
2
6
sin
6
cos2,0For
3
2
1










































 Above the different 3 value of Z are roots of the given function.

9. Hyperbolic Function
Defination of Hyperbolic Function
 
 
 
 
R,x
ee
ee
(x)
(x)
R,x
ee
x
x
R,x
ee
x
x
xx
xx
xx
xx














tanh
as...definedisandtanhbydenotedisxoftangentHyperbolic
2
cosh
as...definedandcoshbydenotedisxofcosineHyperbolic
2
sinh
as...definedandsinhbydenotedisxofsineHyperbolic

10. Hyperbolic Function
Relation between circular & Hyperbolic Function
)1.(..........)sinh()sin(,
)sinh(
2
2
2
2
)sin(
...
2
sin
)()(
xiixTherefore
xi
ee
i
i
ee
i
ee
i
ee
ix
equationaboveinixbyxreplacing
i
ee
x
xx
xx
xx
ixiixi
ixix







 















11. Hyperbolic Function
Relation between circular & Hyperbolic Function
.cot)coth(
,cothcot
,sec)(sec
secsec
,cos)(cos
coscos
,tan)tanh(
tanhtan
,cos)cosh(
coshcos,
xiix
(x)i(ix)
xixh
h(x),(ix)
ecxiixech
ech(x),iec(ix)
xiix
(x),i(ix)
xix
(x),(ix)Similarly











12. Hyperbolic Function
Hyperbolic Identities
   
)(sinh4)sinh(3)3sinh(
)cosh()sinh(2)2sinh(
1)(coth)(cos
)(tanh1)(sec,
.1)(sinh)(cos
1)cosh()sinh(
1)(cos)(sin
...,
1cossin
3
22
22
22
22
22
22
xxx
xxx
xxech
xxhSimilarly
xx
xxi
ixix
aboveinixbyxreplacingNow
xx









13. Hyperbolic Function
Hyperbolic Function for Complex Number
)cosh(
)sinh(
)tanh(
,isfunctionOther
2
)sinh(
as,definedanddenotedisoffunctionsinehyperboliccomplexThe
2
)cosh(
as,definedanddenotedisoffunctioncosinehyperboliccomplexThe
z
z
z
ee
z
z
ee
z
z
zz
zz








14. Example:3
 Prove that ).1ln(sin 21
ziziz 
 
 
).1ln(sin
)1ln(
)1ln(
1ln
1)(ln
)(sinh
)sinh(
sin
,bysidesbothgMultiplyin
.sinsin
Let,
21
2
22
2
2
1
1
ziziz
ziziw
ziziiw
ziziw
iziziw
iziw
iwiz
wiiz
i
wzwz













15. Thank You