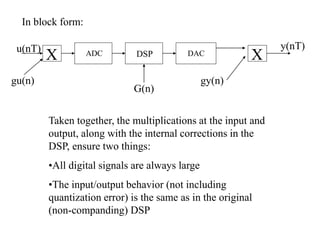
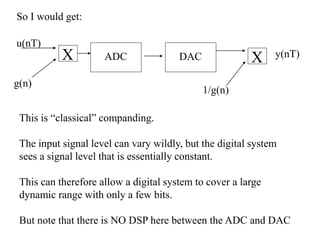
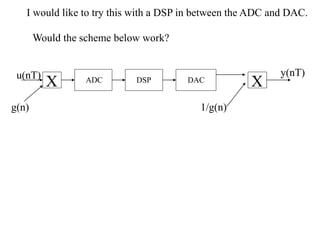
The document discusses companding, a technique to reduce quantization errors in fixed point DSPs. It involves multiplying the input signal by a time-varying gain that is large when the input is small and small when the input is large, to keep the signal level constant. Simply applying this to the input/output of a DSP will distort its behavior. Instead, the states of the DSP must be transformed to also keep them constant, while preserving the original input/output relationship. The author proposes implementing this on a digital reverberator to compare the performance of companded and non-companded versions as the bit depth varies.

1. Companding in Fixed Point DSPs
A scheme to reduce the quantization
(roundoff) errors in Fixed Point DSPs

2. ADVANTAGE OF LARGE
SIGNALS
• When the signals in the DSP are large, they
take full advantage of the available bits.
• When the signals in the DSP are small, only
a few of the available bits are used.
• The roundoff error is essentially
independent of the signal level, so the
distortion due to roundoff is much worse for
small signals

3. To reduce roundoff error, I
would like to keep all digital
signals as large as possible at all
times.

4. Since the system has a set
overflow tolerance, I would
like all digital signals to have a
roughly constant envelope,
where the constant is slightly
lower than the system
overflow tolerance

5. Suppose I have analog input, u(t), and analog
output, y(t), so I need an ADC and a DAC:
ADC DAC
u(t) y(t)

6. Consider multiplying the analog input by a time
varying signal, g(n), which is LARGE when the
input signal is SMALL, and SMALL when the
input signal is LARGE, so that I get a roughly
constant envelope signal
For example, if env(n) is the (sampled) envelope
of the input, g(n) could be k/env(n) where k is
some constant slightly lower than the system
overflow tolerance level.

7. If g(n) is LARGE when u(nT) is SMALL, and SMALL
when u(nT) is LARGE, then g(n)*u(nT) stays at a
roughly constant signal level, and can be set large always.
I would therefore like to multiply my input by g(n)
BEFORE it gets to the ADC, so that the ADC ALWAYS
sees a large signal.

8. To preserve the input/output behavior (but with less
quantization noise), I would like to multiply the output signal
by 1/g(n).
The multiplication by 1/g(n) should come AFTER the DAC so
that THE SIGNAL STAYS LARGE WHENEVER IT IS
DIGITAL.

9. ADC DAC
u(nT)
y(nT)
So I would get:
X
g(n)
X
1/g(n)
This is “classical” companding.
The input signal level can vary wildly, but the digital system
sees a signal level that is essentially constant.
This can therefore allow a digital system to cover a large
dynamic range with only a few bits.
But note that there is NO DSP here between the ADC and DAC

10. I would like to try this with a DSP in between the ADC and DAC.
Would the scheme below work?
ADC DAC
u(nT) y(nT)
g(n)
X
1/g(n)
DSP
X

11. NO! Using classical companding
on a DSP will horribly distort the
input/output behavior
Taking a DSP, multiplying its input by
a time-varying signal g(n), and then
multiplying the output by 1/g(n) will,
in general, CHANGE the input/output
behavior of the DSP (dramatically)

12. For example, let y(n)=u(n-k)
So the DSP is a k-sample delay.
If I do:
ADC DAC
u(nT) y(nT)
g(n)
X
1/g(n)
Z-k
X
•The output is now g(n-k)*u(n-k)/g(n)
•This is NOT equal to u(n-k).
•It is DISTORTED by the factor g(n-k)/g(n).
•This is a time-varying distortion.
•More complicated systems will have more complicated distortions

13. All is not lost: I can preserve
input/output behavior by making
internal corrections in the DSP

14. I want the internal states to be large for all n,
so I will do a change of basis in the state space:
w(n)=G(n)*x(n)
Consider a system given
by:
x(n+1)=A*x(n)+B*u(n)
y(n)=C*x(n)+D*u(n)

15. w(n)=G(n)*x(n) so x(n)=G-1(n)*w(n)
w(n+1)=G(n+1)*x(n+1)=
G(n+1)*A*x(n)+G(n+1)*B*u(n)=
[G(n+1)*A* G-1(n)]*w(n)+[G(n+1)*B]*u(n)
y(n)=[C*G-1(n)]*w(n)+D*u(n)
This is a new internally time-varying system,
whose states are always large, but whose
input/output behavior is identical to the original
system’s!

16. In block form:
ADC DAC
u(nT) y(nT)
gu(n)
X
gy(n)
DSP
X
G(n)
Taken together, the multiplications at the input and
output, along with the internal corrections in the
DSP, ensure two things:
•All digital signals are always large
•The input/output behavior (not including
quantization error) is the same as in the original
(non-companding) DSP

17. •Multiplies the input by a signal (based on the G(n) matrix), which
ensures that the signal at the ADC is always large.
•Makes internal corrections to the states of the DSP to ensure that the
states are always large.
•Multiplies the output of the DAC by another signal (based on G(n)).
This is necessary, since companding ensures that the output of the DAC
is always large, while the actual output will not always be large.
•These modifications do NOT change the input/output behavior (they
only lower the quantization error).
Companding for DSPs

18. Project Proposal
•Implement companding on an actual
DSP – a simple digital reverberator

19. Project Proposal (cont’d)
• For a given output “quality” how many bits
are needed in the original, non-companding
DSP versus in the companding DSP?
• For a given number of bits, how does the
output “quality” compare between the
original, non-companding DSP versus the
companding DSP?

20. Project Proposal (cont’d)
• Can I quantify the improvements?
For example:
•Mean square error of output
•SNR (as a function of signal level)
•Harmonic distortion in spectrum
I would like to find all these for both the companding and the
non-companding systems as a function of the number of bits
used in the system.