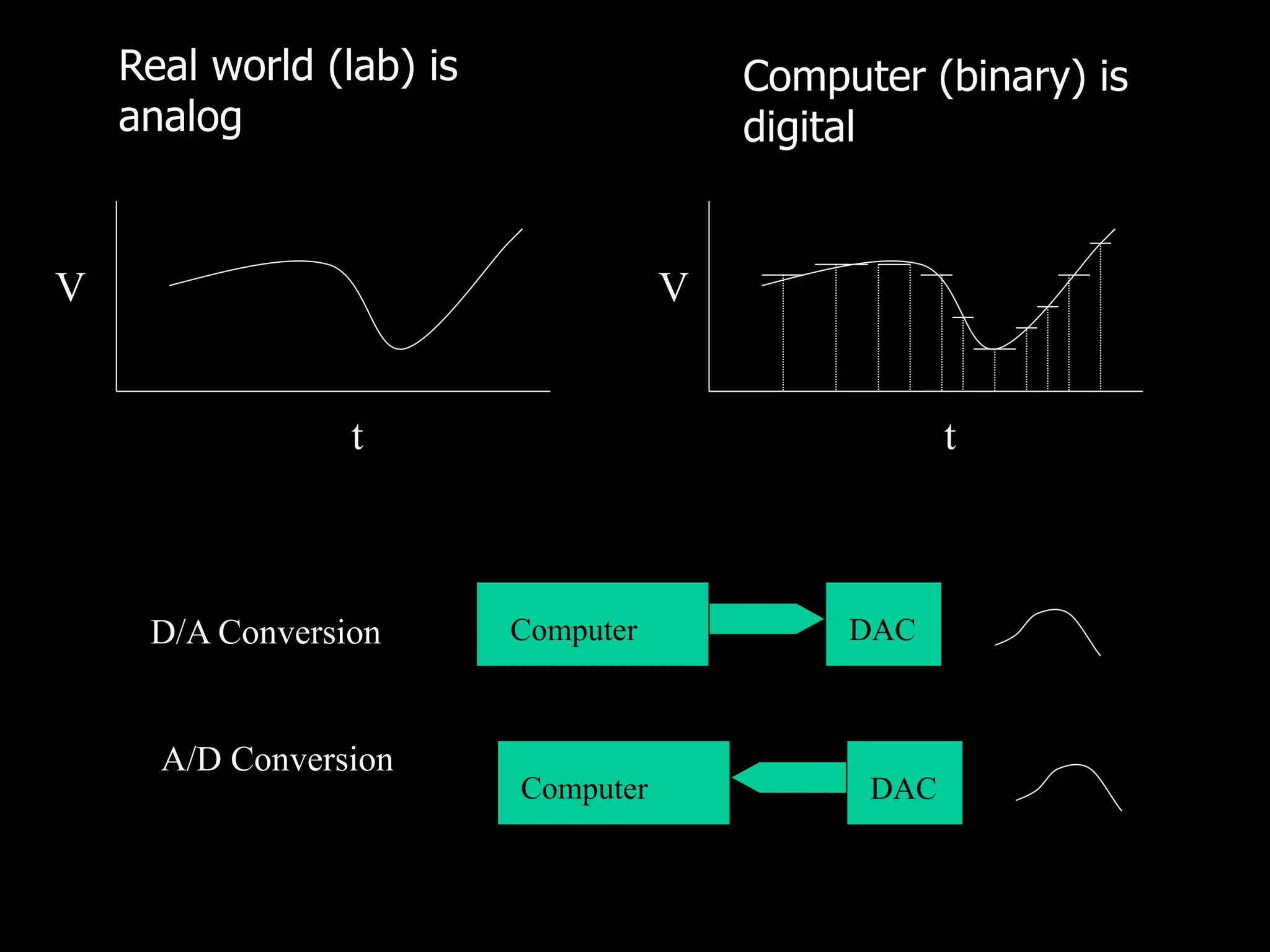
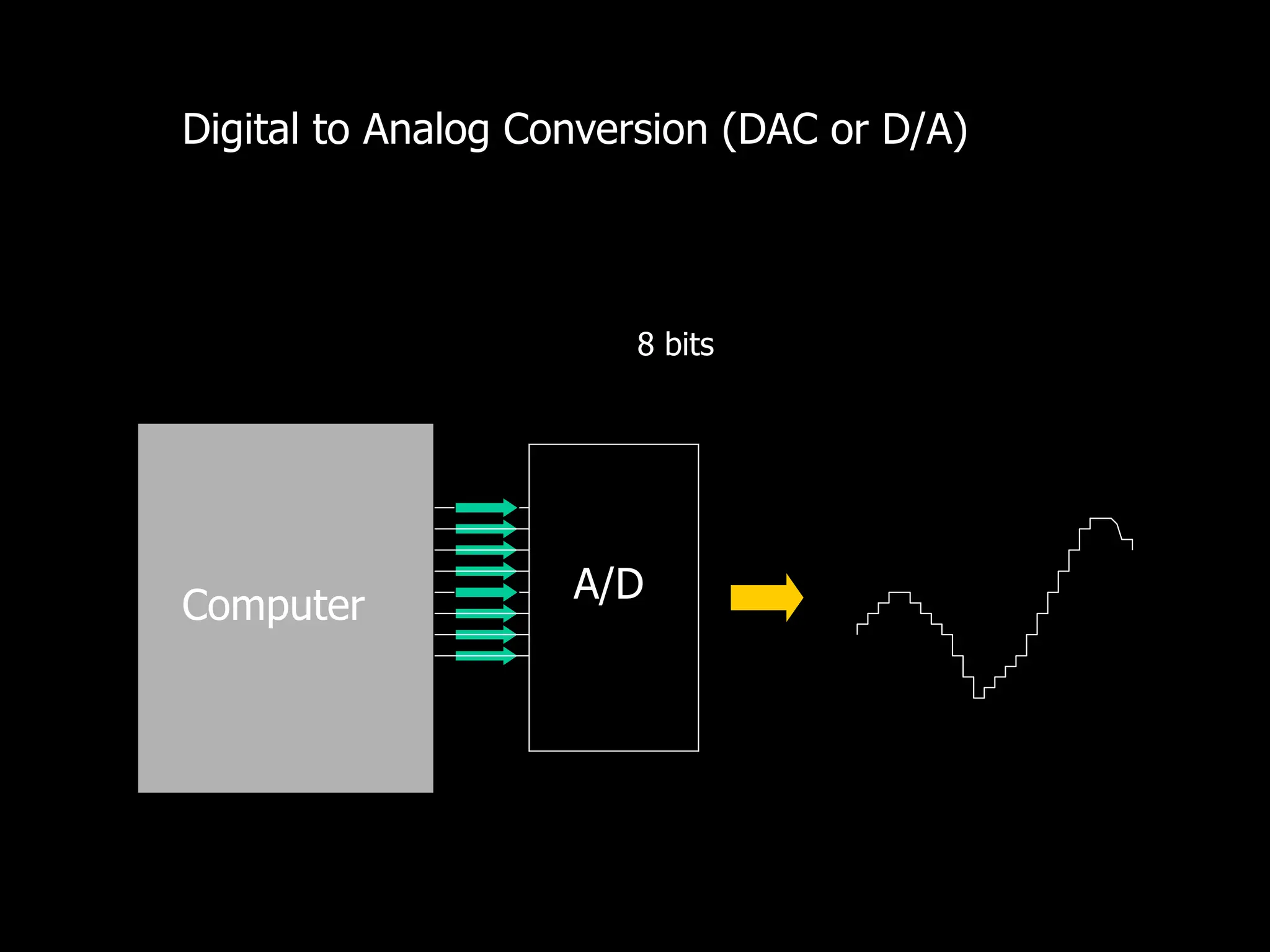
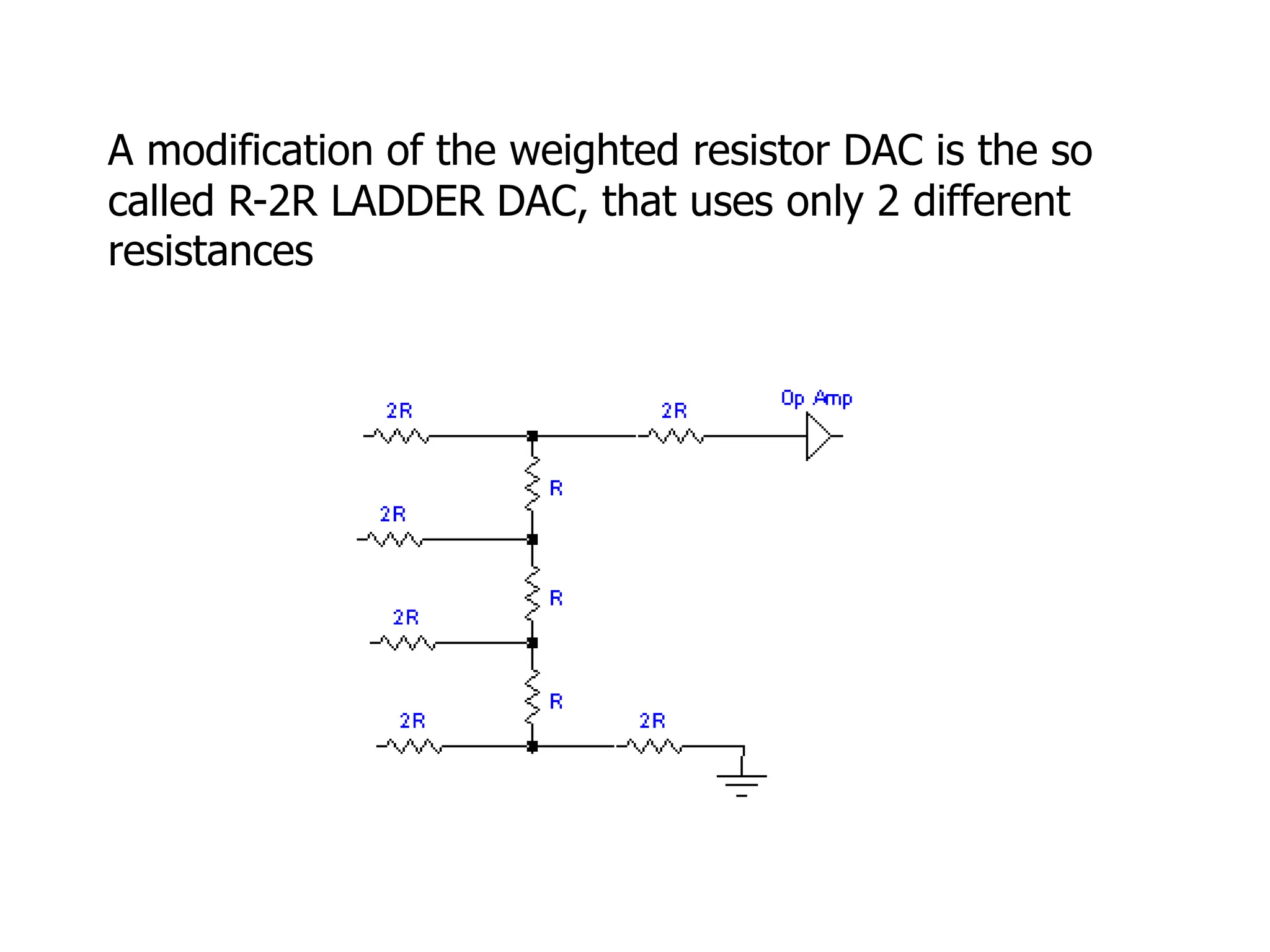
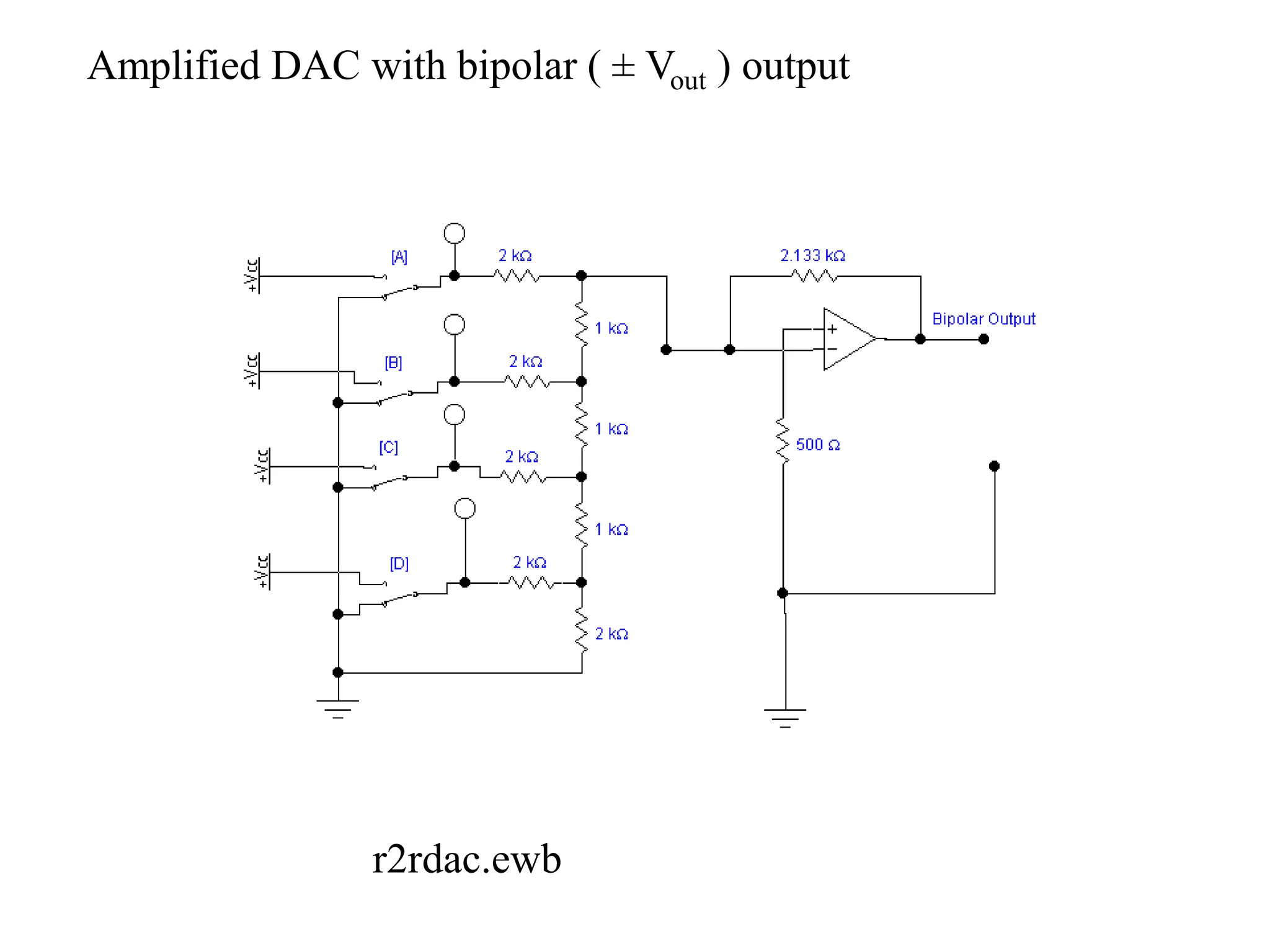
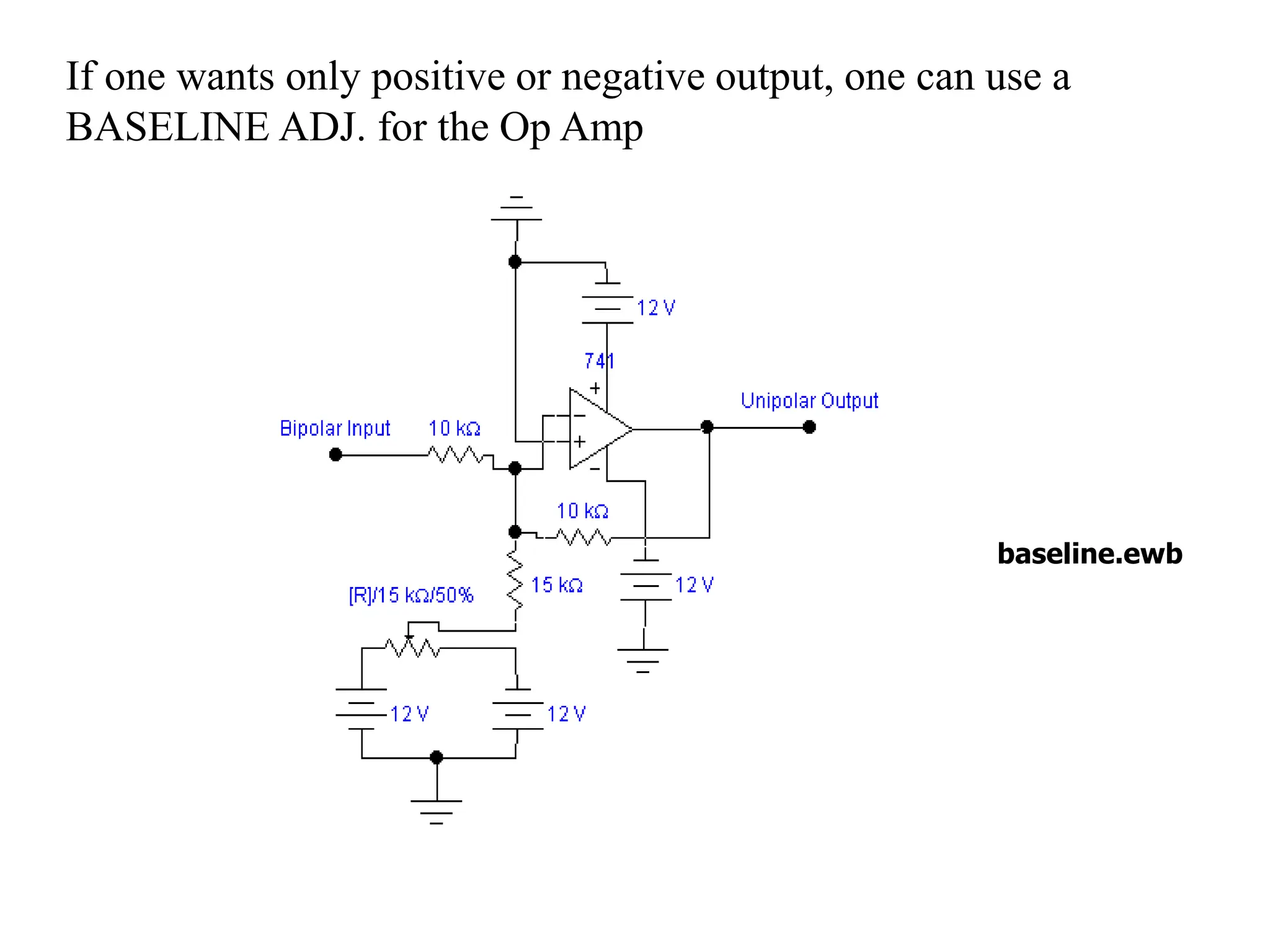
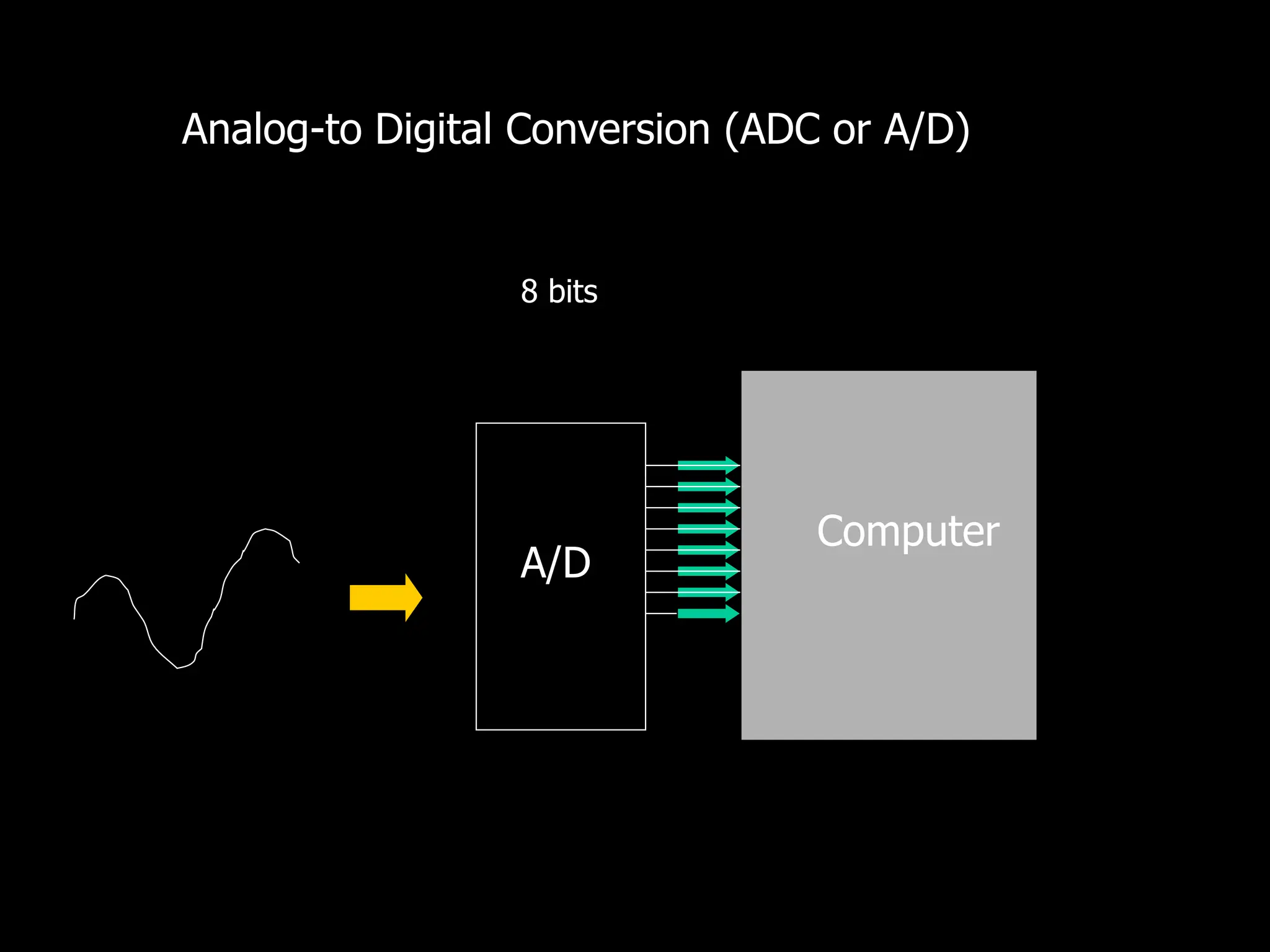
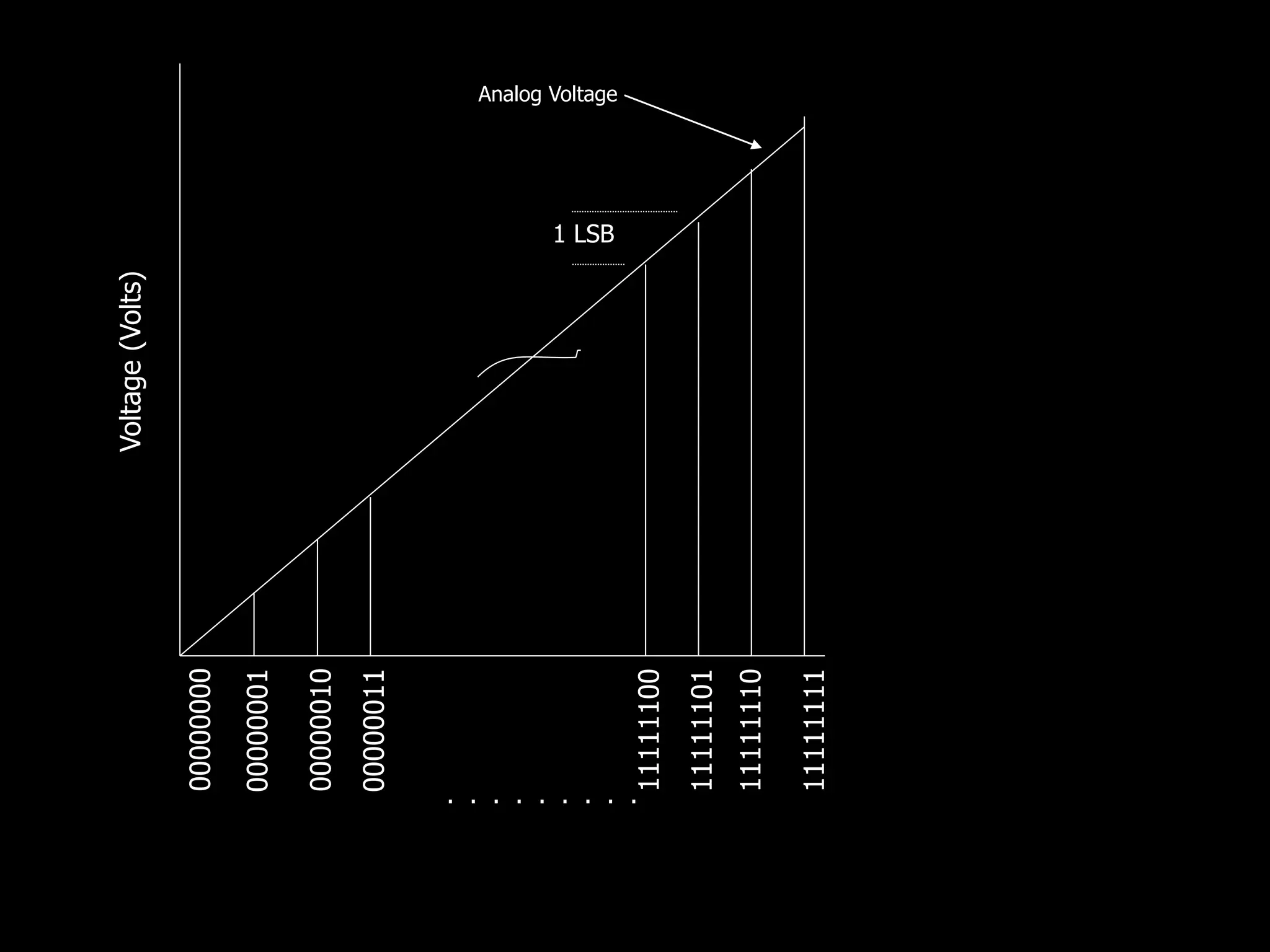
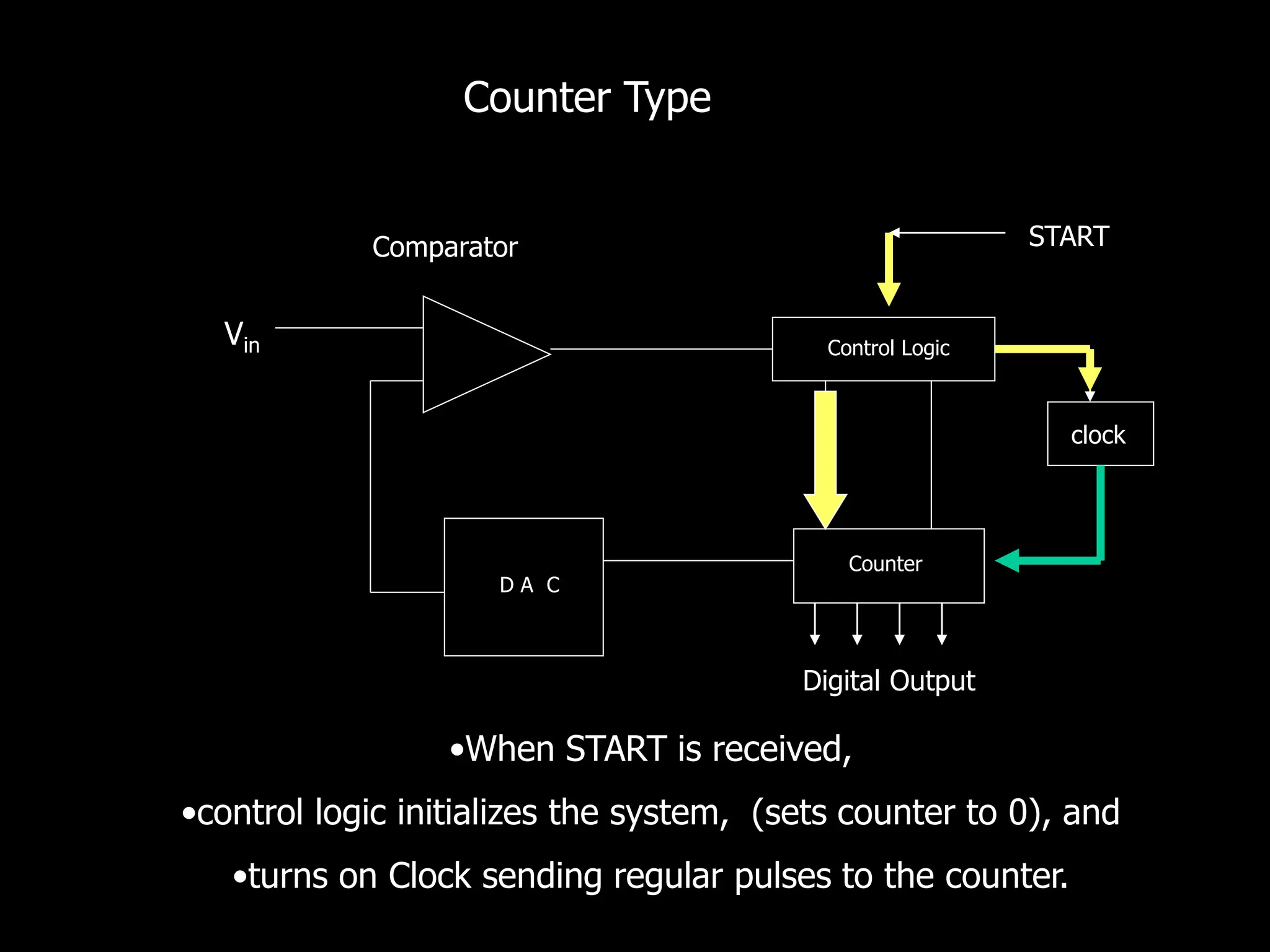
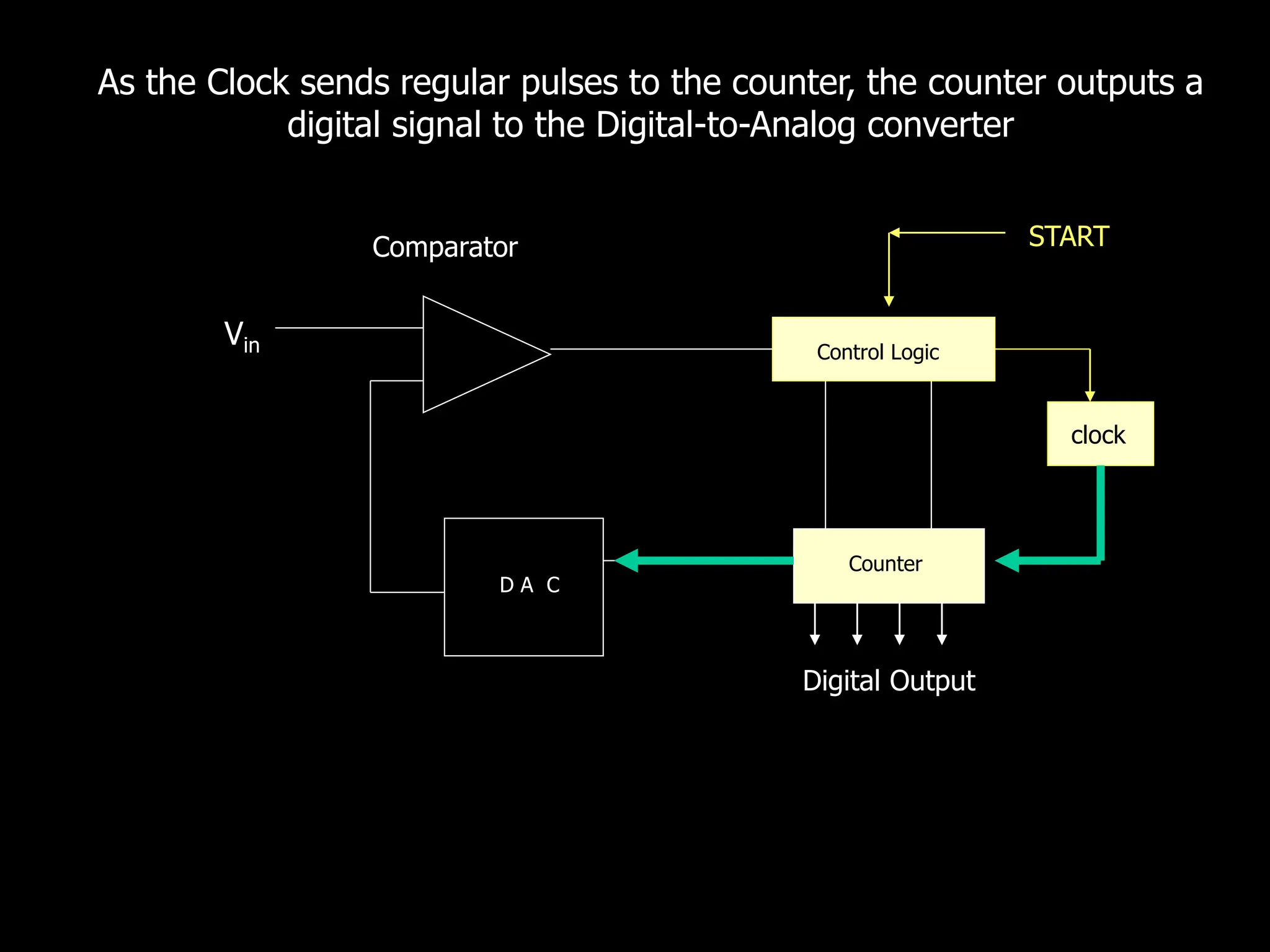
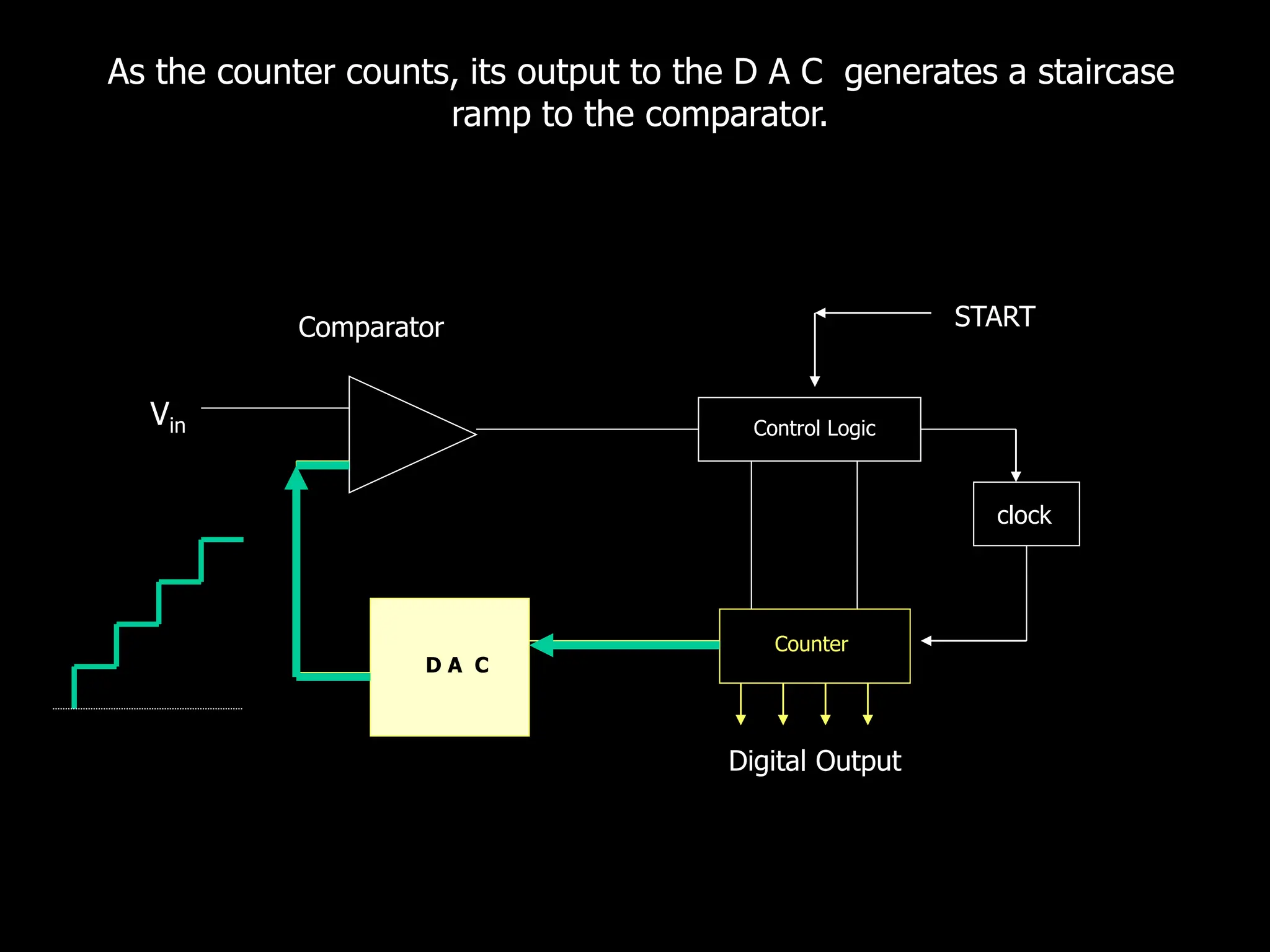
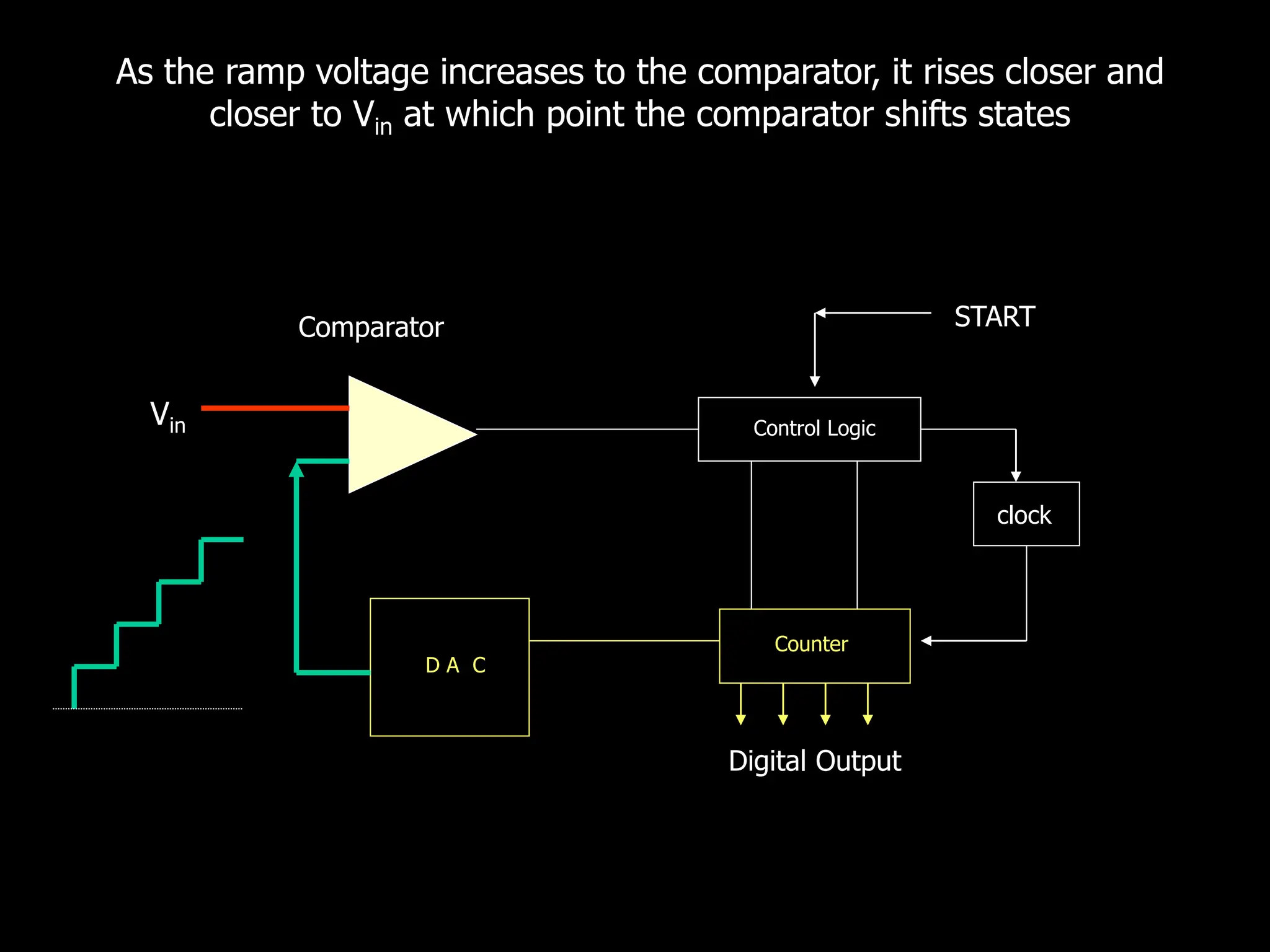
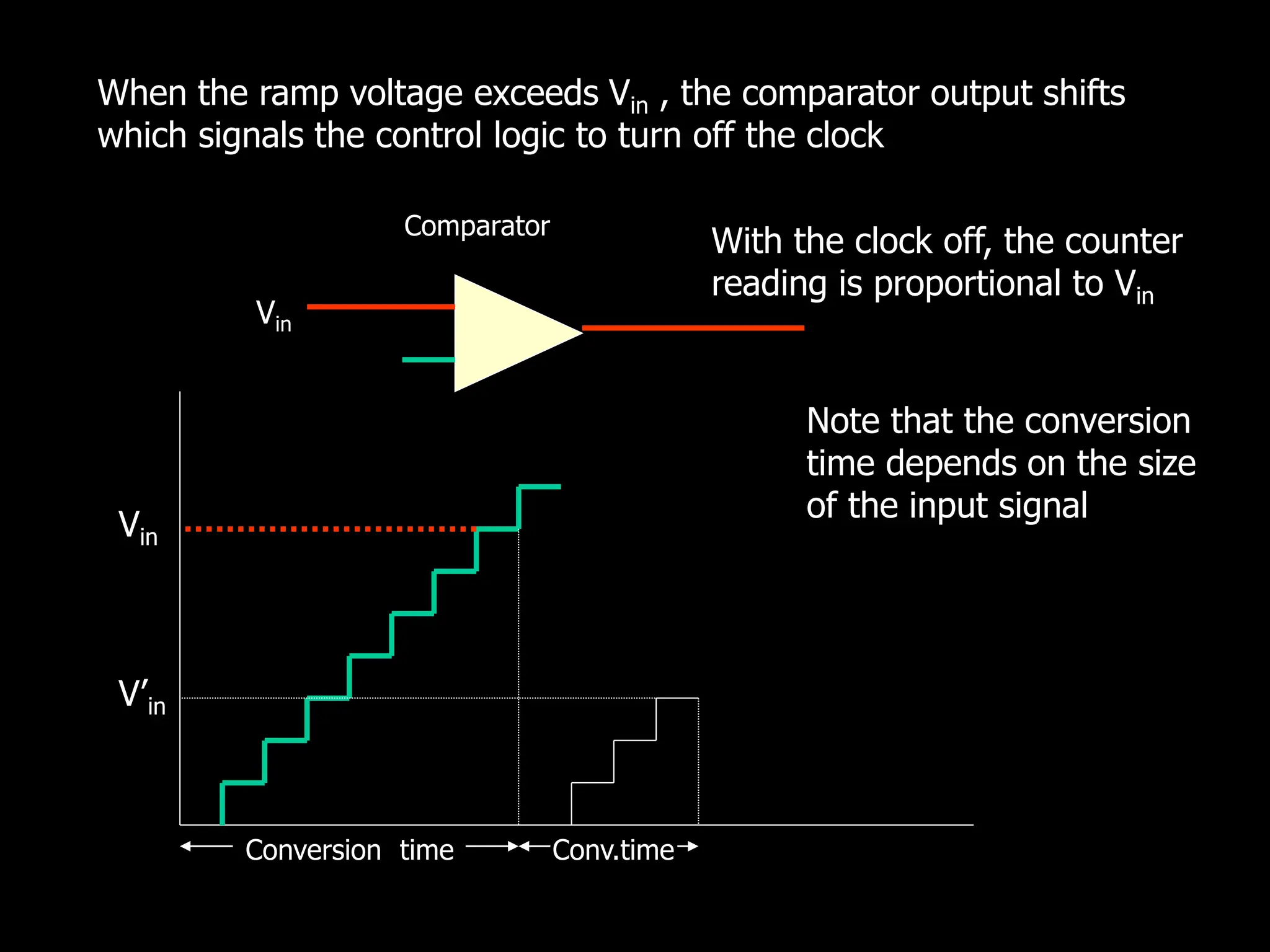
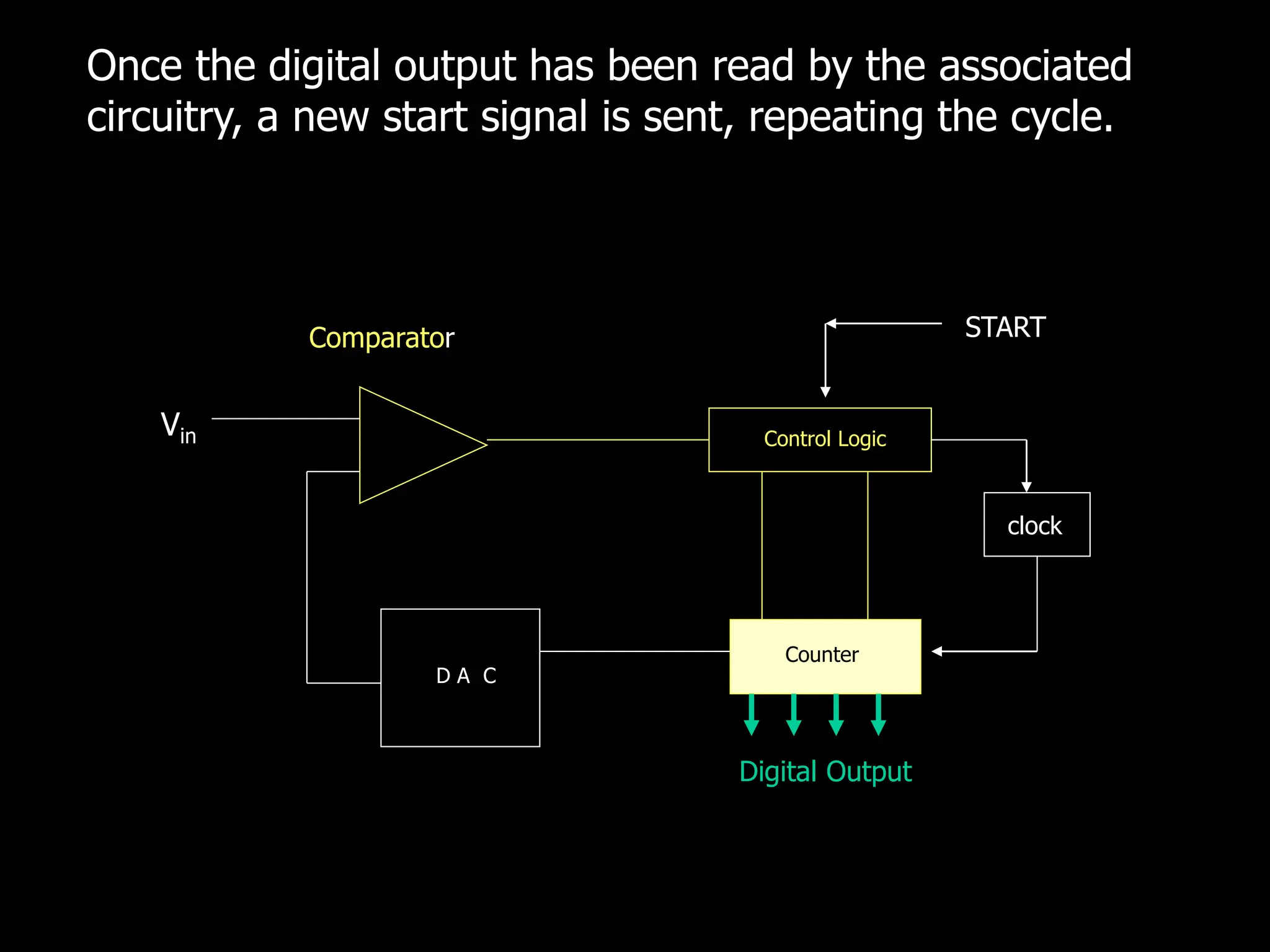
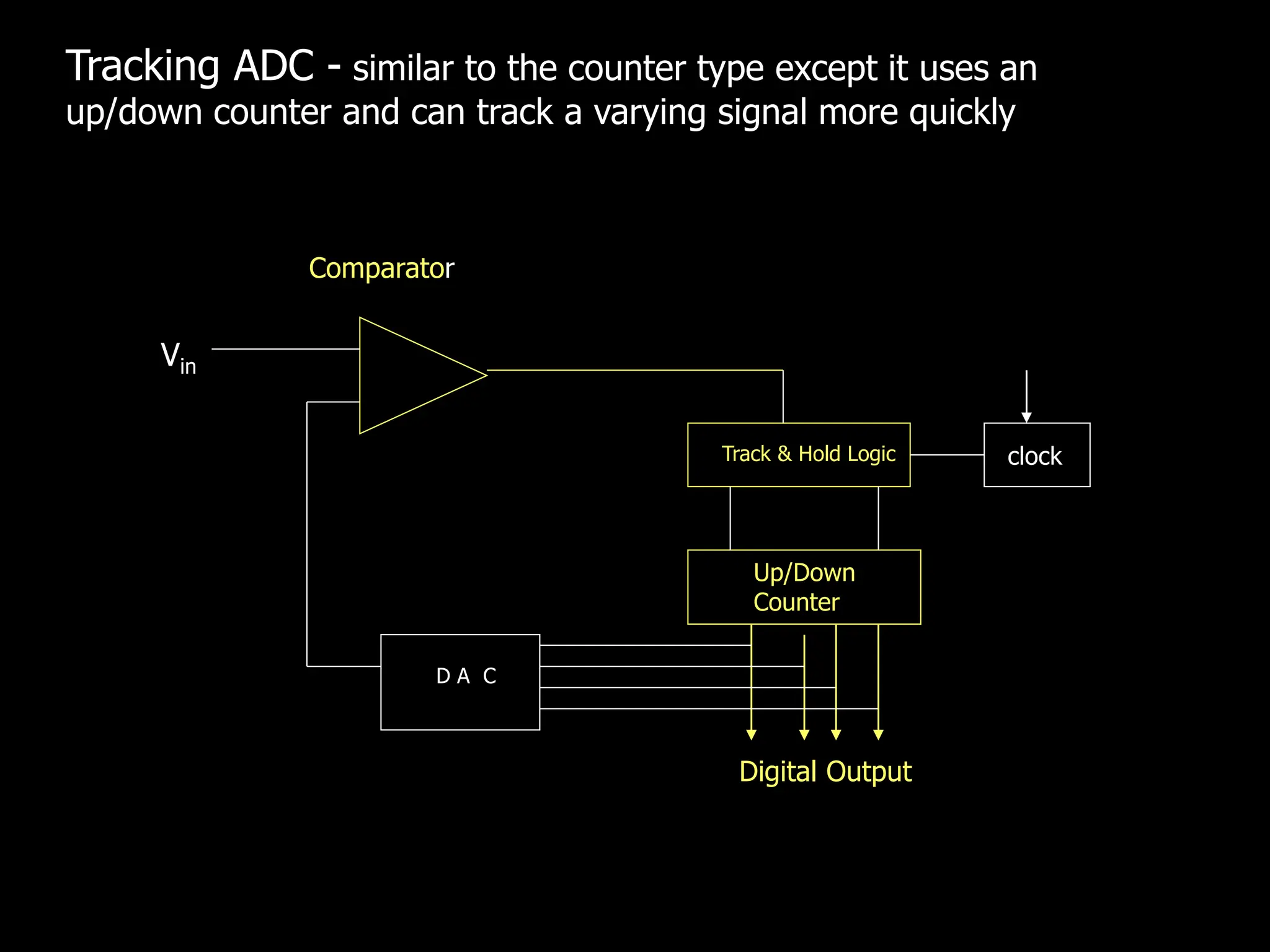
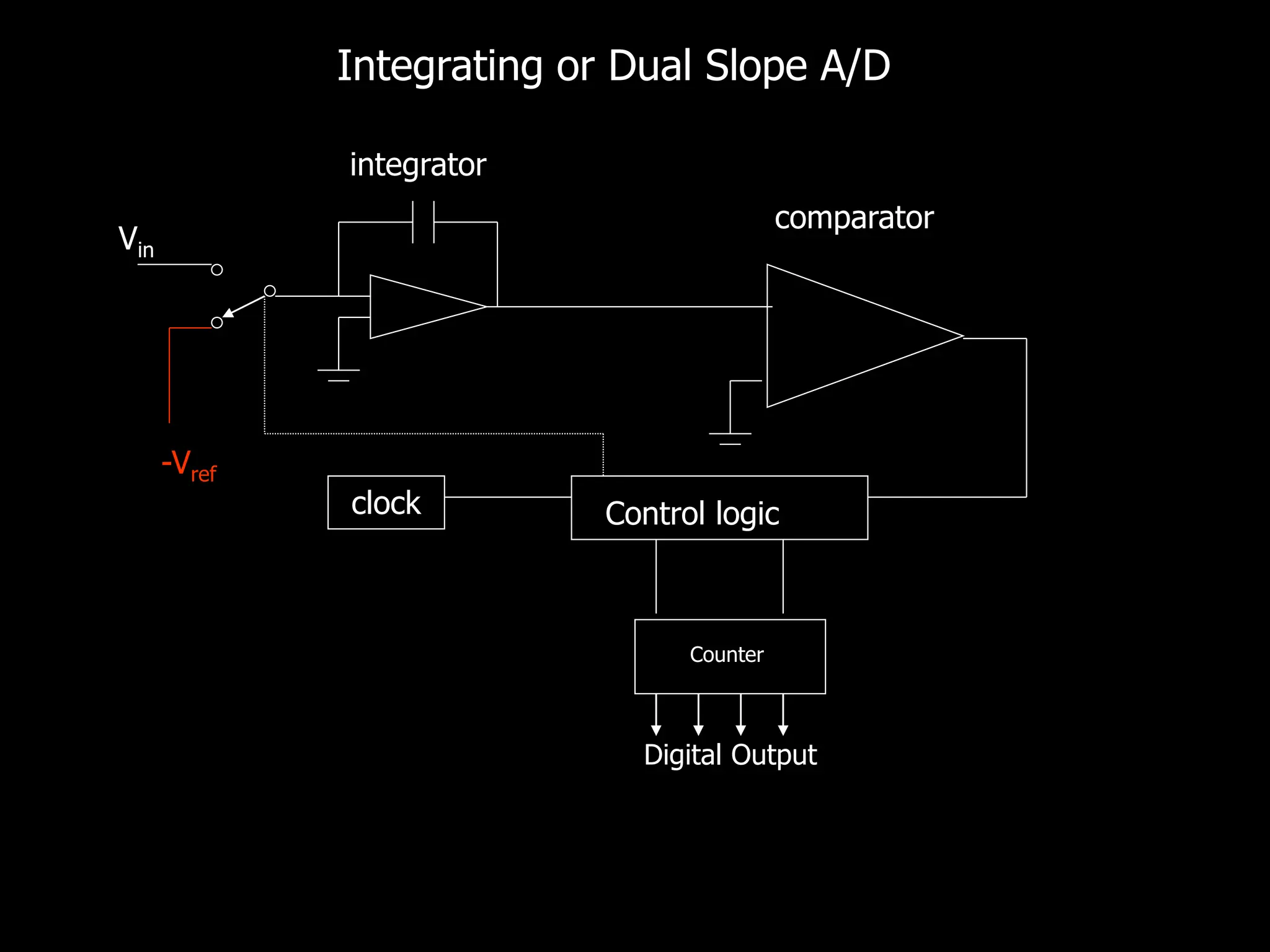
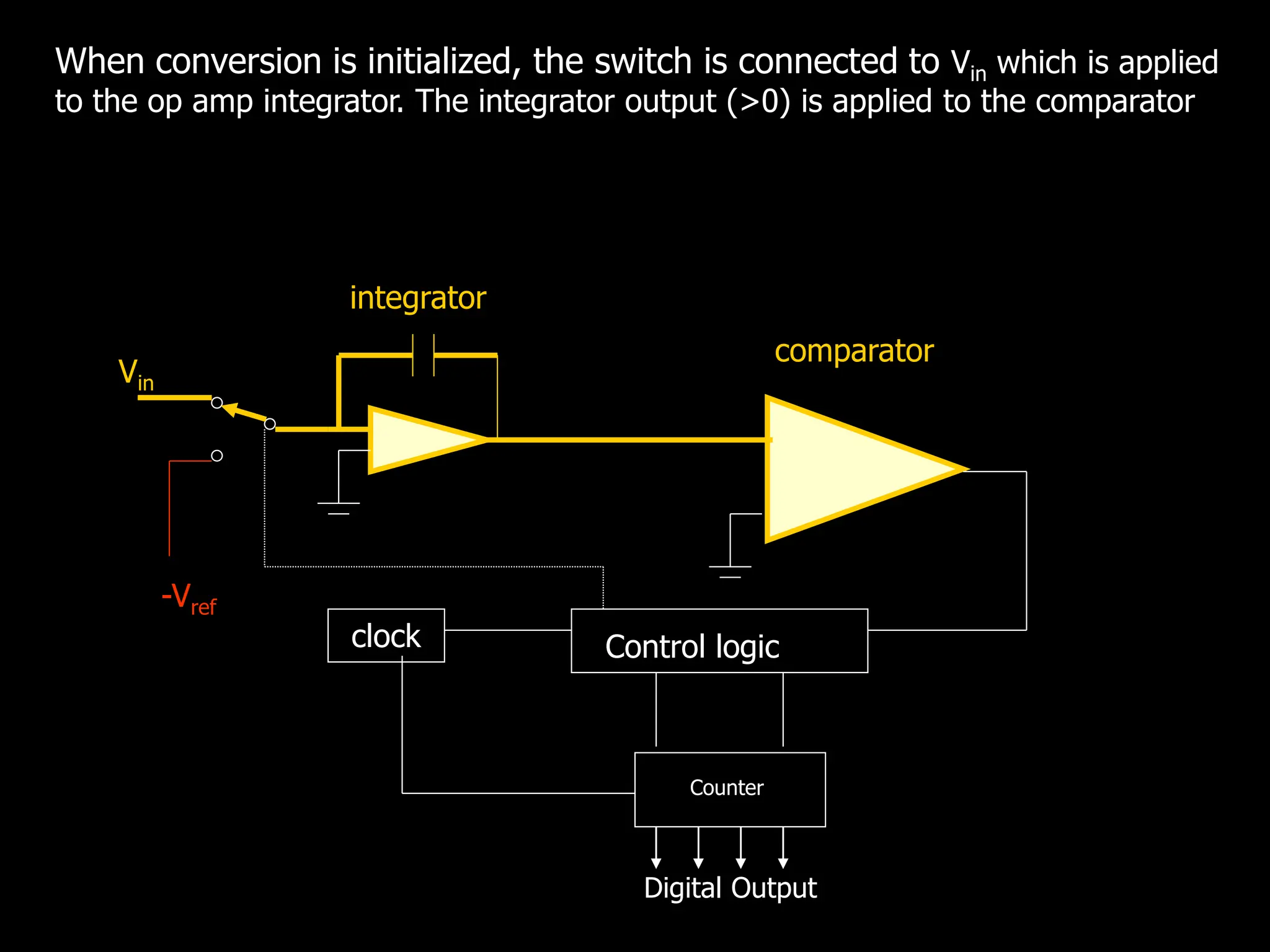
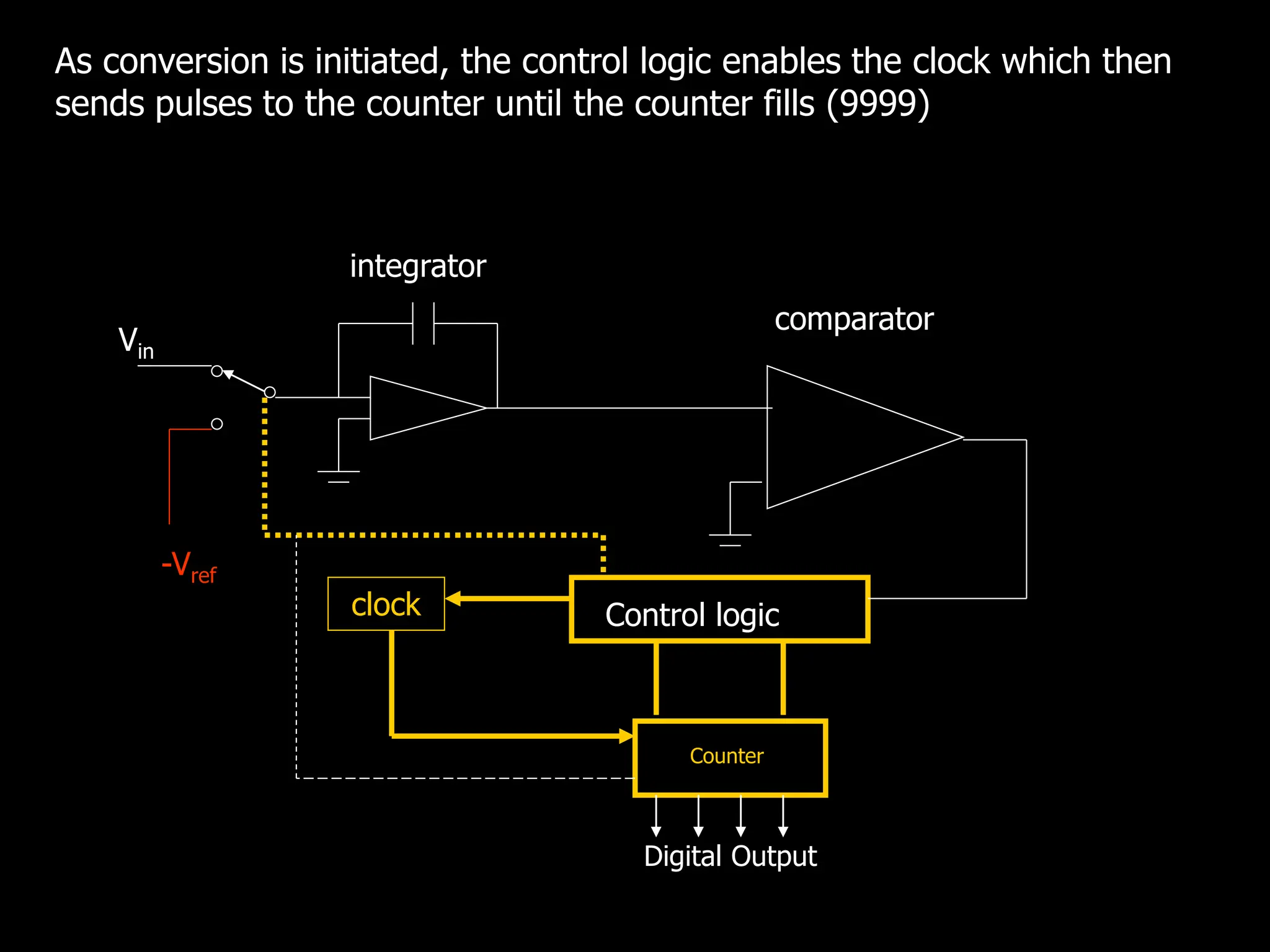
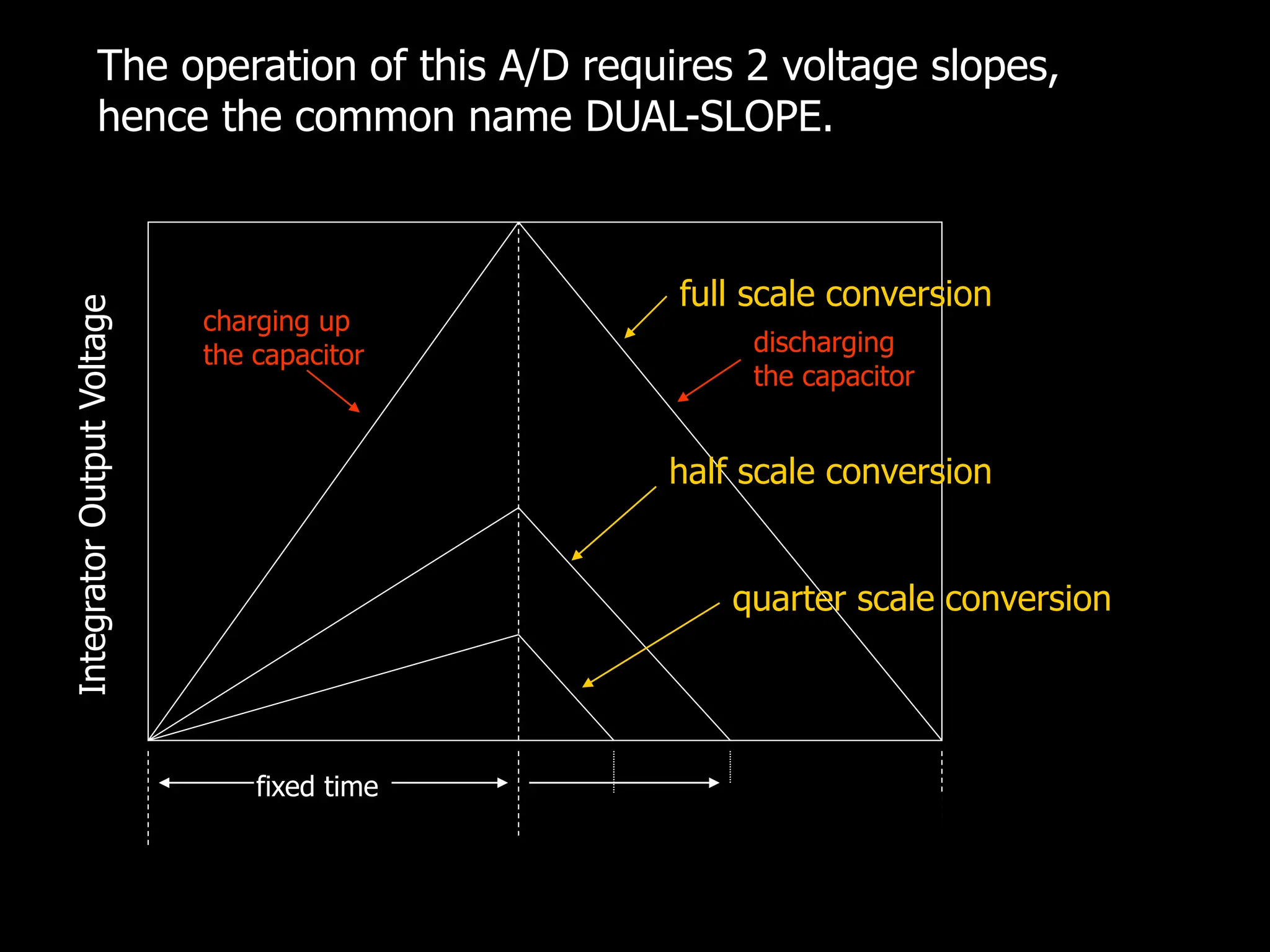
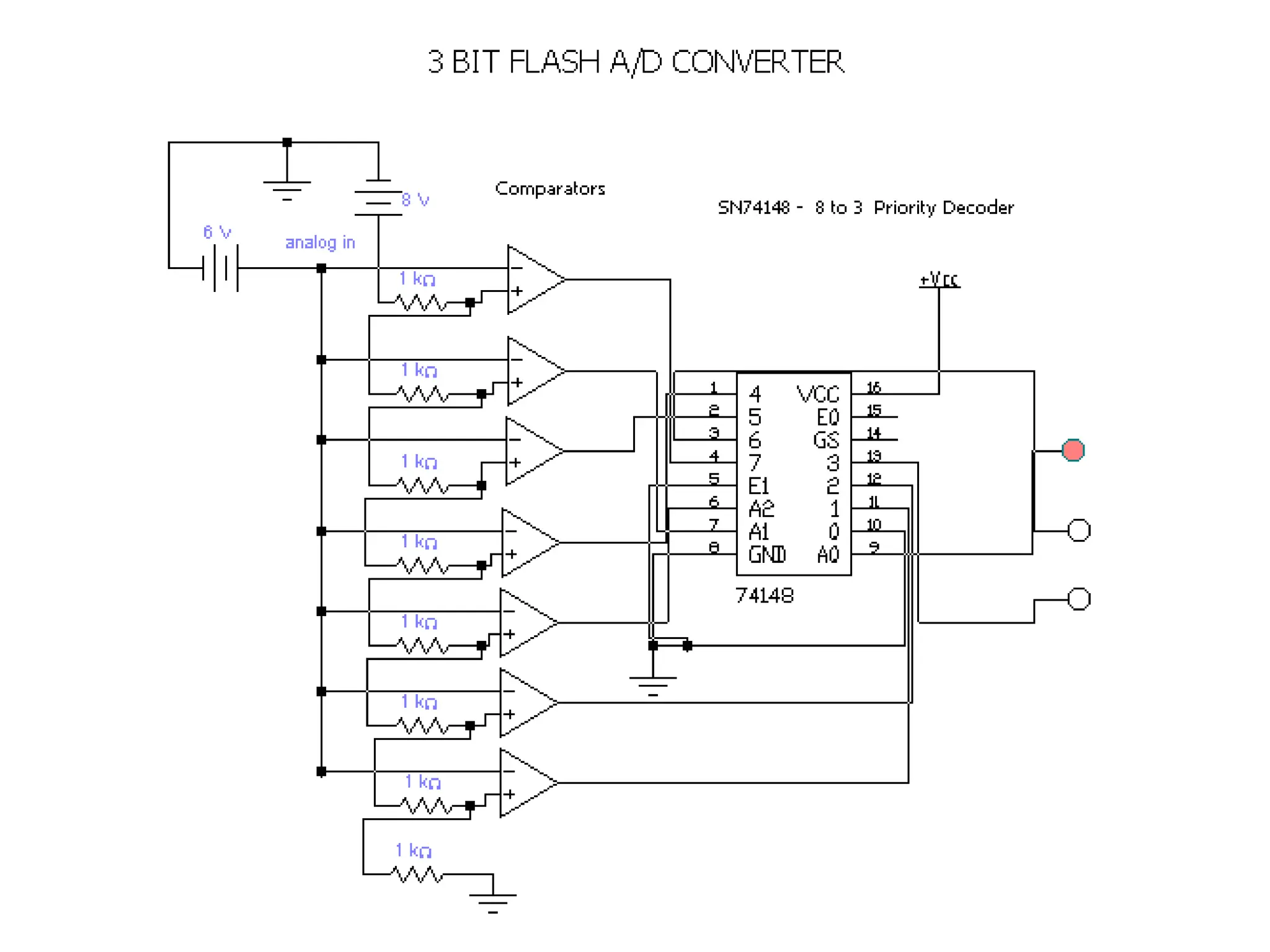
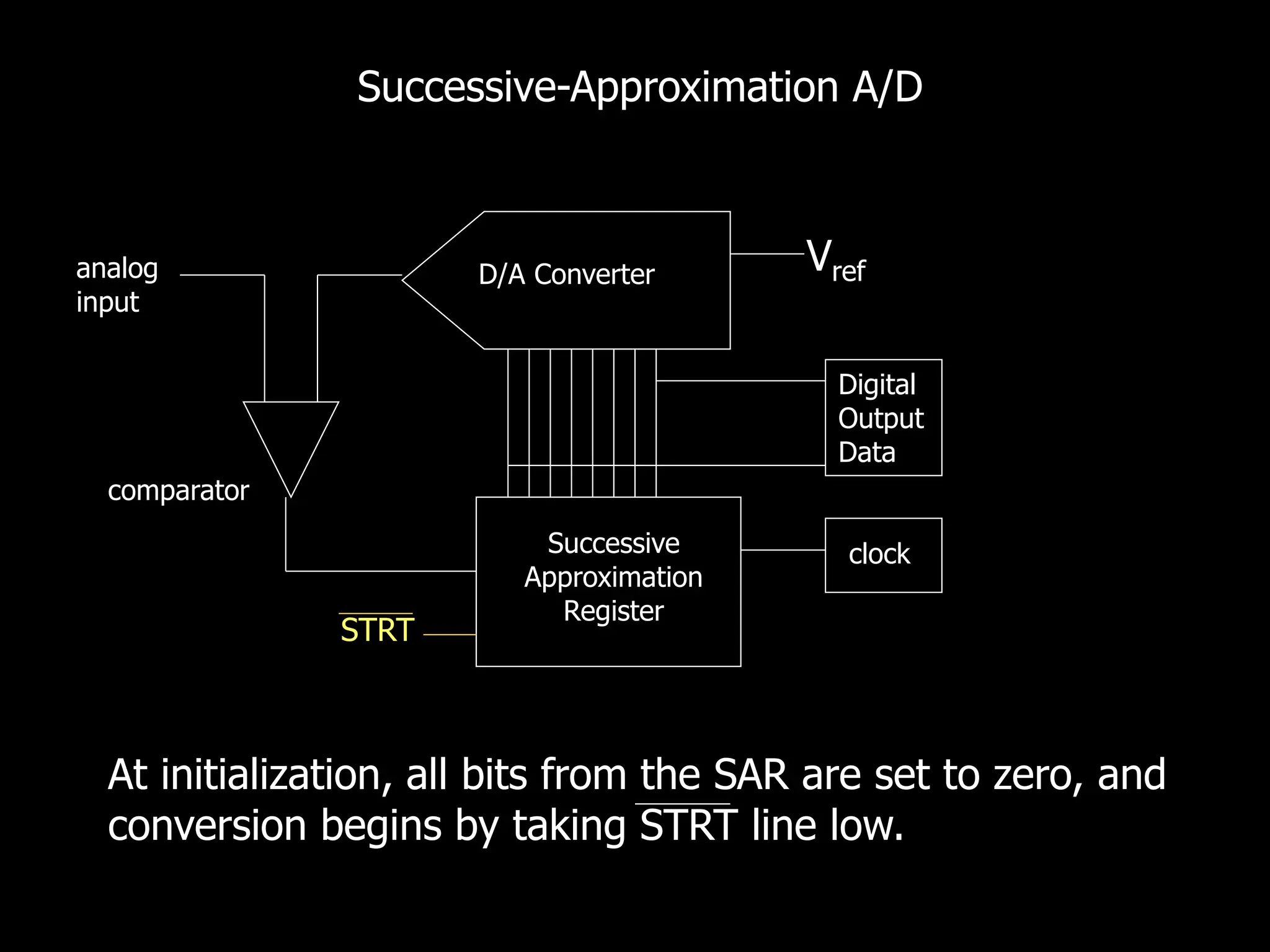
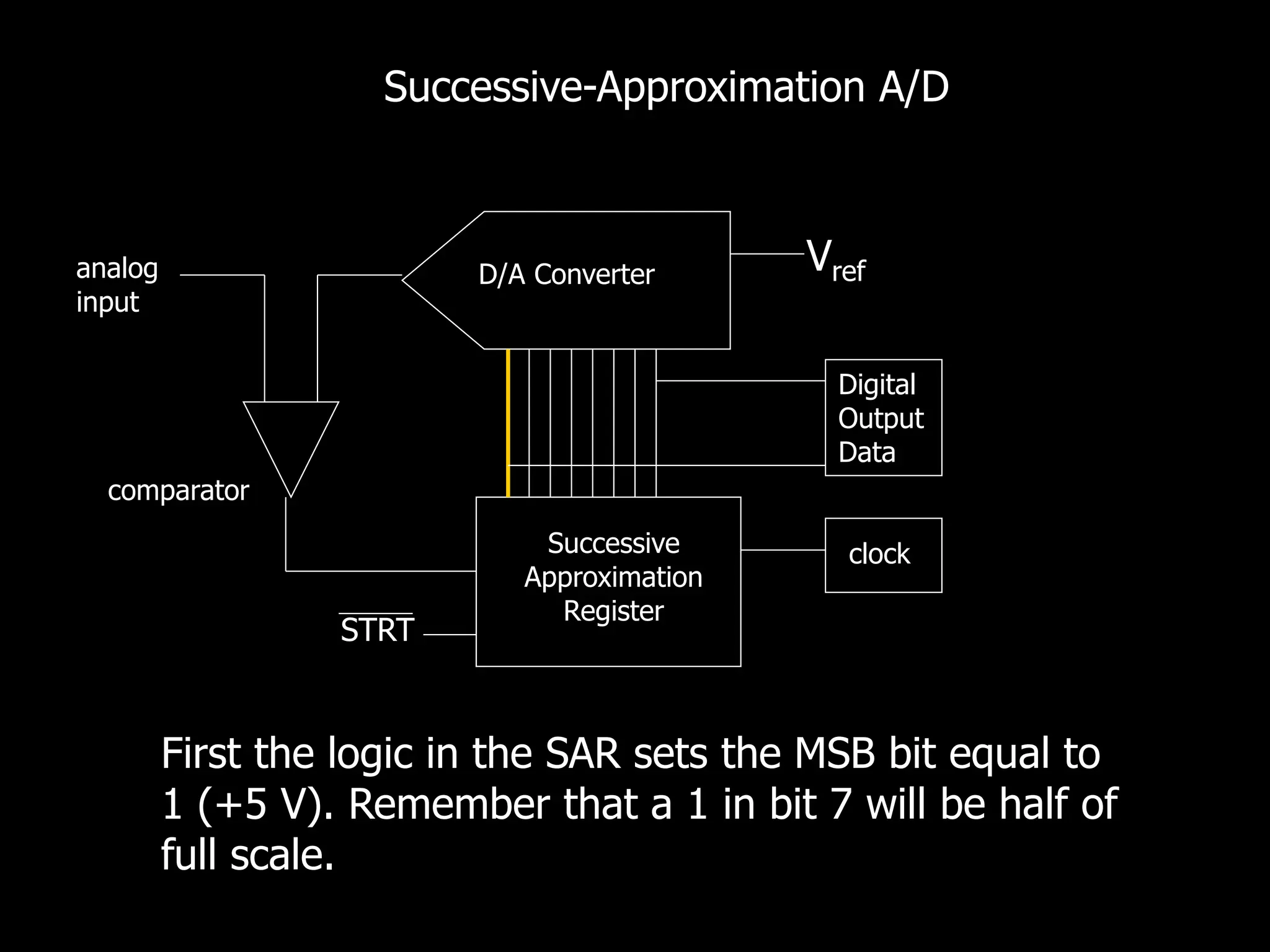
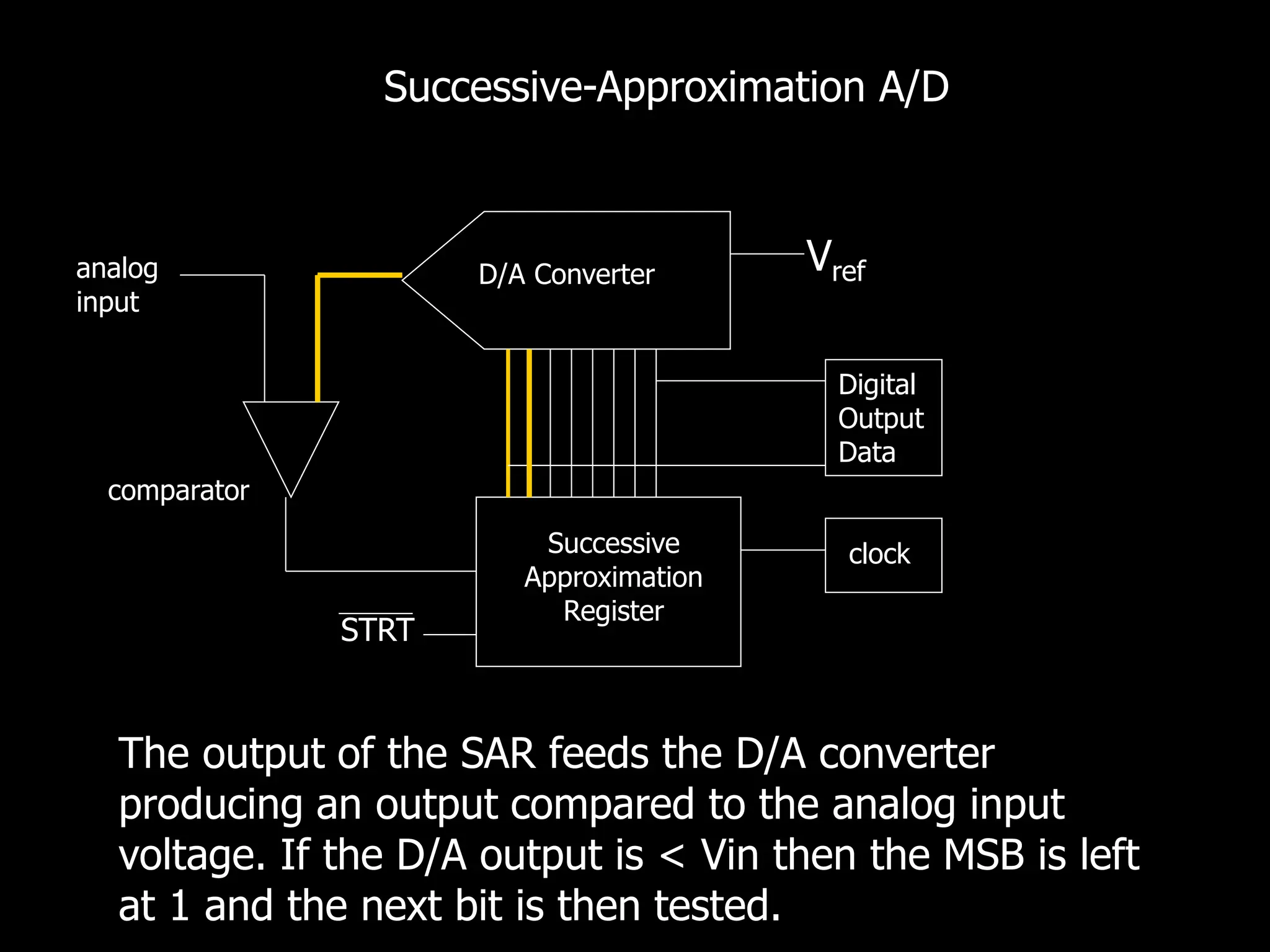
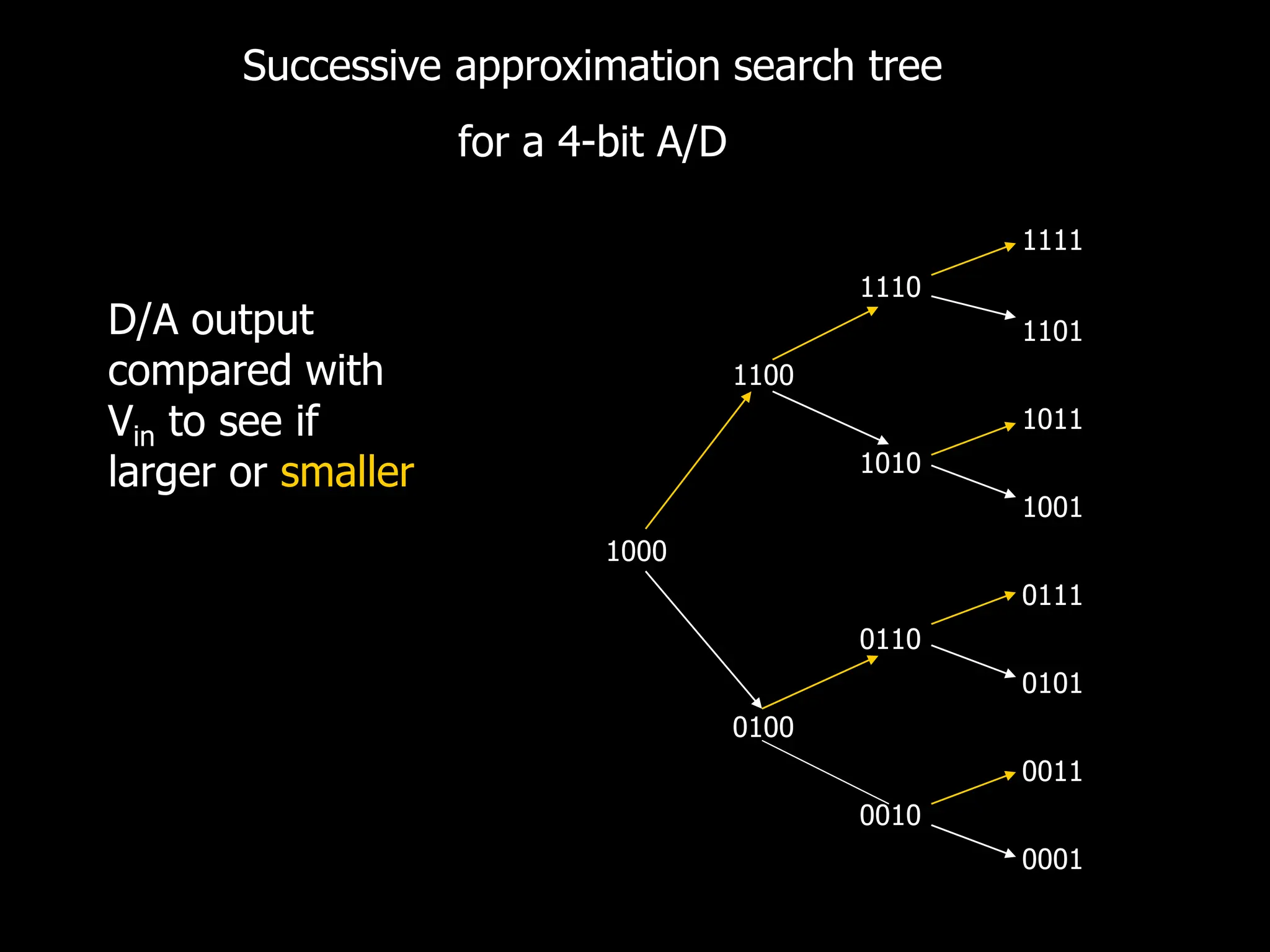
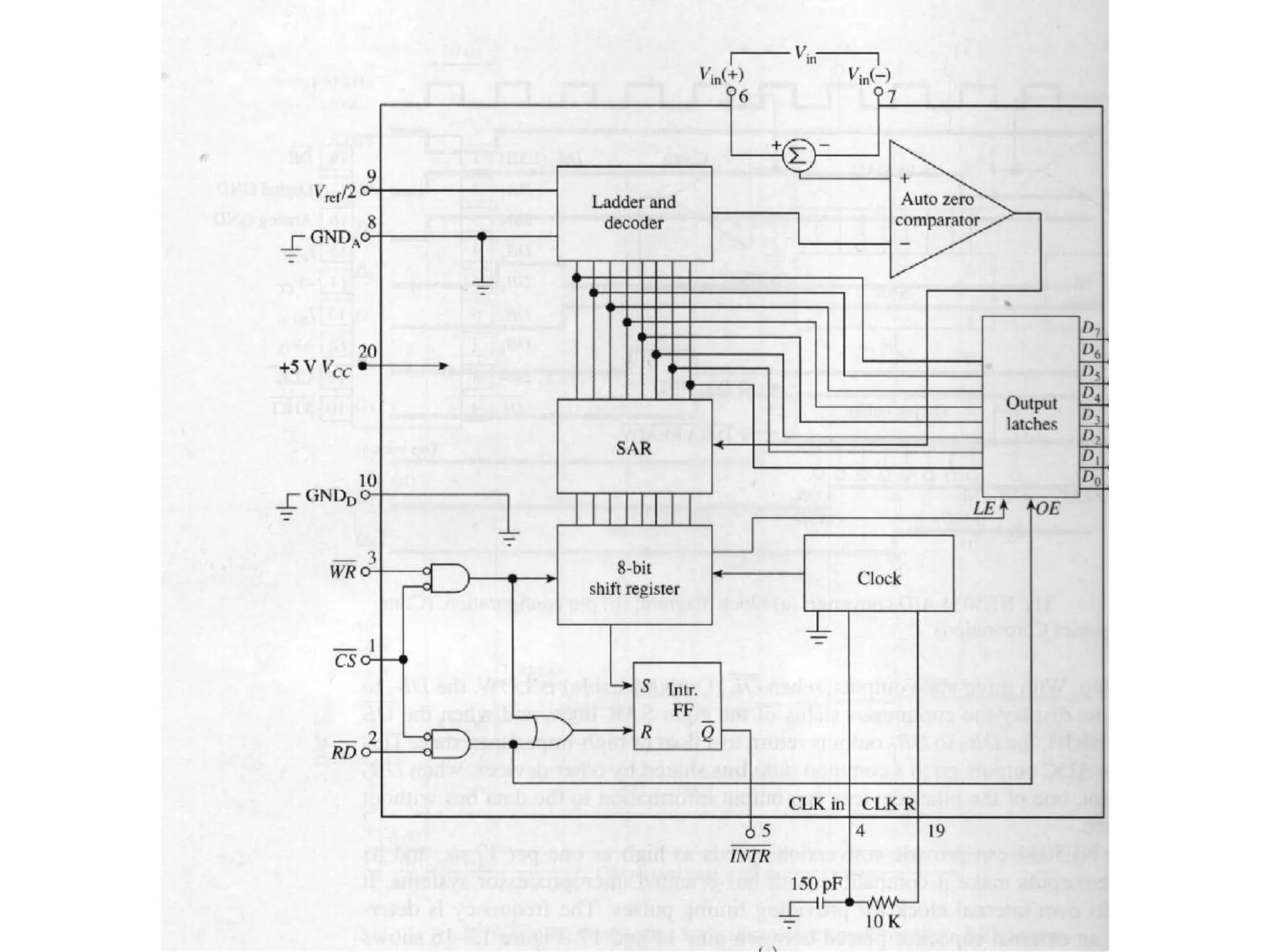
This document discusses digital to analog conversion (DAC) and analog to digital conversion (ADC). It explains that DAC converts a digital signal from a computer into an analog voltage. This can be done using a resistor ladder network or R-2R ladder. ADC converts a real-world analog voltage into a digital number that a computer can process. Common ADC types include counter, dual-slope integrating, flash, and successive approximation. Successive approximation ADCs are widely used as they provide good speed and accuracy at a reasonable cost.