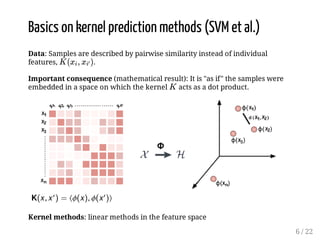
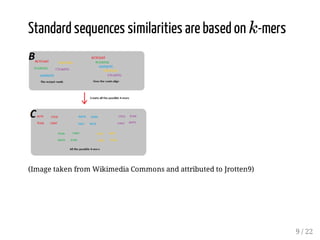
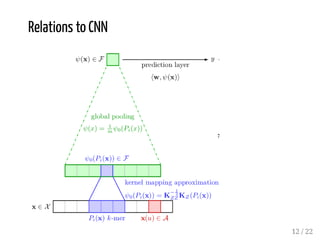
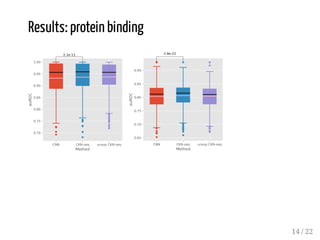
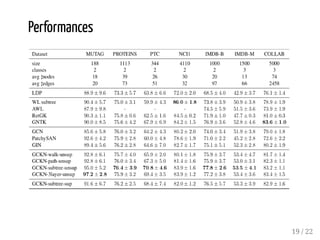
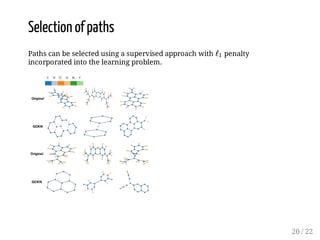
This presentation discusses how convolutional kernel networks (CKNs) can be used to model sequential and graph-structured data through kernels defined over sequences and graphs. CKNs define feature maps from substructures like n-mers in sequences and paths in graphs into high-dimensional spaces, which are then approximated to obtain low-dimensional representations that can be used for prediction tasks like classification. This approach is analogous to convolutional neural networks and can be extended to multiple layers. The presentation provides examples showing CKNs achieve good performance on problems involving protein sequences and social networks.

1. Convolutional networks and graph networksConvolutional networks and graph networks
through kernelsthrough kernels
Nathalie Vialaneix, INRAE/MIATNathalie Vialaneix, INRAE/MIAT
WG GNN, September 24th, 2020WG GNN, September 24th, 2020
1 / 221 / 22

2. A description oftwo referencesA description oftwo references
Chen, Jacob, Mairal (2019) Biological sequence modeling with convolutionalChen, Jacob, Mairal (2019) Biological sequence modeling with convolutional
kernel networks.kernel networks. BioinformaticsBioinformatics, 35(18): 3294-3302., 35(18): 3294-3302.
Chen, Jacob, Mairal (2020) Convolutional kernel networks for graph-structuredChen, Jacob, Mairal (2020) Convolutional kernel networks for graph-structured
data.data. Proceedings of ICML 2020Proceedings of ICML 2020..
2 / 222 / 22

3. Topic
(What is this presentation about?)
sequence data are used to predict a numerical variable or a class
sequences are vectors of dimension
examples:
protein homology: predicting the family of a protein from its
sequence
using DNA sequence to predict if the site is a TF binding site
[0, 1]
|A|×L
3 / 22

4. Topic
(What is this presentation about?)
labeled graph data are used to predict a numerical variable or a class
examples:
social networks (collaboration networks or actor networks): ego-
networks of collaborators or actors are obtained from different fields
(collaborations) or different movie types. How to predict the field /
movie type of a given network only from its structure?
molecules classifications: molecules are represented by labelled
graphs and used to predict a chemical property (mutagenicity)
4 / 22

5. Topic
(What is this presentation about?)
Main idea: connexion between kernel prediction methods with specific
kernels for sequences or graphs and convolutional neural networks.
5 / 22

6. Basics on kernel prediction methods (SVM et al.)
Data: Samples are described by pairwise similarity instead of individual
features, .
Important consequence (mathematical result): It is "as if" the samples were
embedded in a space on which the kernel acts as a dot product.
Kernel methods: linear methods in the feature space
K(xi , xi
′ )
K
6 / 22

7. An example ofkernel regression method: kernel ridge
regression
(1) is the mean square loss (as for standard linear regression) in the
feature space where is simply when this
feature space is of finite dimension
(2) is a penalty that forces to be "smooth"
The solution is given by:
(where we know the explicit form of the )
minw∈H ∑
n
i=1
(yi − ⟨ϕ(xi ), w⟩)
2

(1)
+ λ∥w∥
2

(2)
1
n
⟨ϕ(xi ), w⟩ ∑
p
j=1
wjϕj(xi )
p
w
prediction(x) = ⟨w
∗
, ϕ(x)⟩ = ∑
n
i=1
αi K(x, xi )
αi
7 / 22

8. CKN for sequencesCKN for sequences
8 / 228 / 22

9. Standard sequences similarities are based on -mers
(Image taken from Wikimedia Commons and attributed to Jrotten9)
k
9 / 22

10. Using -mers to compute sequence kernels
where:
is the -mer (for a given ) at position in (so every -mer in
is compared to every -mer in )
computes a similarity between two given -mers. A standard version
is simply: 1 if the two -mers are identical and 0 otherwise. The article
proposes a continuous relaxation.
And this kernel can be used to define a kernel regression machine... that is
very similar to convolutional neural network ("masks" passed on a small
subsequences and then combined).
k
K(xi , xi
′ ) = ∑
j,j
′ K0 (Pj(xi ), Pj
′ (xi
′ ))
1
mm
′
Pj(xi ) k k j xi k xi
k xi
′
K0 k
k
10 / 22

11. Simpli cation...
Main idea: defines a feature map from the set of -mers into a large
dimensional space. Approximate this feature map to obtain a mapping into a
small dimensional space that provides interpretability.
How to do that? Select -mers that are used as "representers" for
all -mers and approximate:
K0 ϕ0 k
R
q
q k z1 , … , zq
k
ϕ0 (Pj(xi )) ≃ ψ0 (Pj(xi )) K
−1/2
0Z

q×q matrix based on zl
K0Z (Pj(xi ))

q×q matrix based on zl andPj(xi)
11 / 22

12. Relations to CNN
12 / 22

13. Extensions
The selected -mers can be chosen in a supervised way during the
training (alterning network learning with selection of -mers) and thus
provides a set of "relevant logo" that explain
The approach can be extended to multiple layers (iterating over the
previously described process)
k
k
Y
13 / 22

14. Results: protein binding
14 / 22

15. Results: motifsearch
15 / 22

16. CKN for graphsCKN for graphs
16 / 2216 / 22

17. Kernel for graphs
The main idea is very similar and based on general definitions of kernels for
graphs:
x are graphs (instead of sequences)
graphs are divided into paths (of length ) starting at node instead of -
mers starting at position
This gives:
and is the set of all paths starting at
is further decomposed into:
k j k
j
K(xi , xi
′ ) = ∑
j,j
′ Kb(Lj(xi ), L
′
j
(xi
′ ))
Lj(xi ) j
Kb
Kb(Lj(xi ), L
′
j
(xi
′ )) = ∑
P ∈Lj(xi),P
′
∈Lj′ (xi′ )
K0 (P , P
′
)
17 / 22

18. Kernel between labelled paths
In graph kernel, is simply a 0/1 similarity (the two paths are identical or
not) which is here relaxed into:
using the labels of the th node along the paths and
The same approximation (here using a selection of paths) can thus be used to
define a representation of the network that can be used for prediction.
Implemented in https://github.com/claying/GCKN
K0
K0 (P , P
′
) = exp(−γ ∑
k
l=1
∥label(l) − label(l)∥
2
)
label(l) l P P
′
18 / 22

19. Performances
19 / 22

20. Selection ofpaths
Paths can be selected using a supervised approach with penalty
incorporated into the learning problem.
ℓ1
20 / 22

21. That's all for now...That's all for now...
... questions?... questions?
21 / 2221 / 22

22. References
Micheli A (2009) Neural networks for graphs: a contextual constructive approach. IEEE
Transactions on Neural Networks, 20(3): 498-511
Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G (2009) The graph neural network
model. IEEE Transactions on Neural Networks, 20(1): 61-80
Sperduti A, Starita A (1997) Supervised neural network for the classification of structures.
IEEE Transactions on Neural Networks, 8(3): 714-735
22 / 22