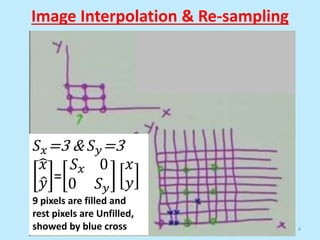
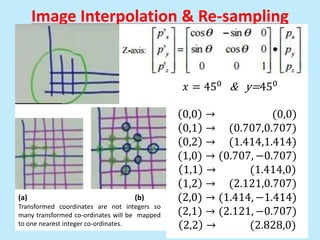
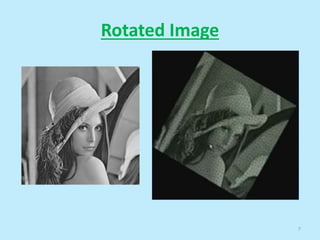
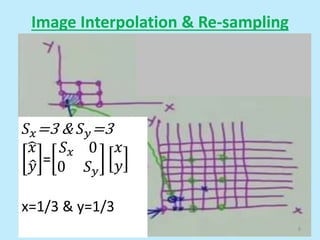
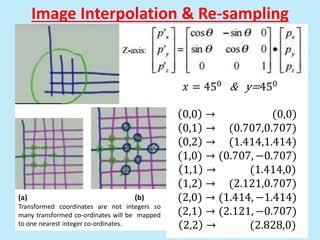
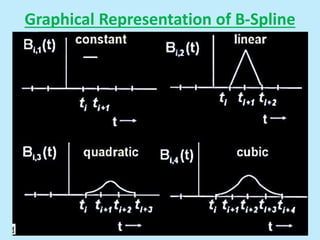
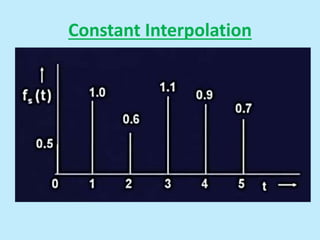
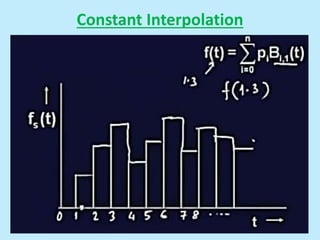
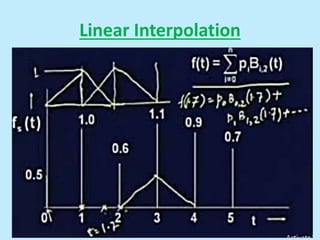
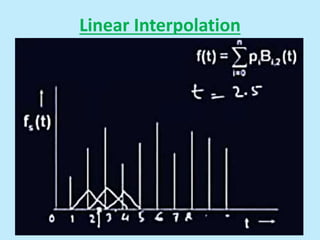
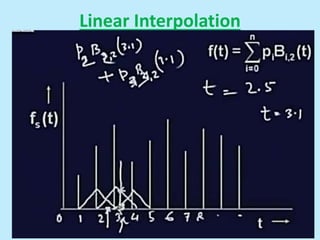
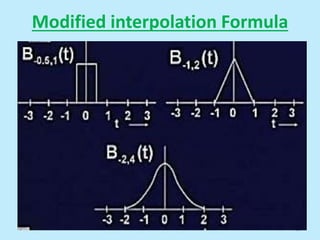
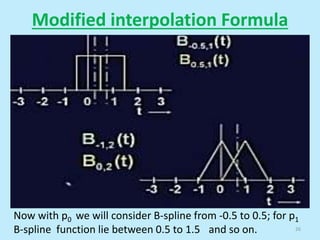
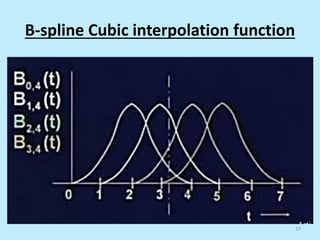
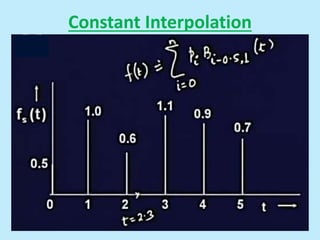
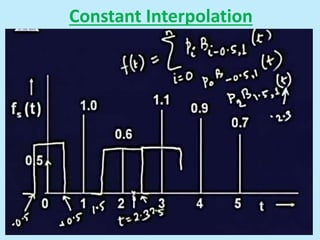
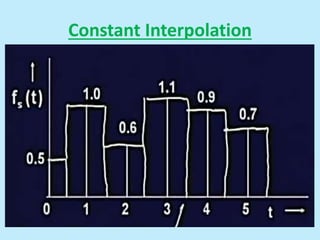
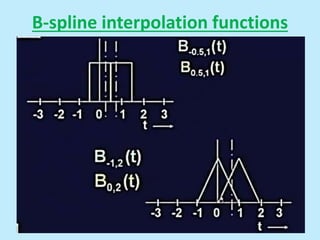
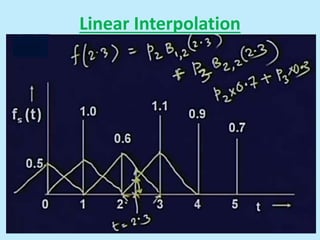
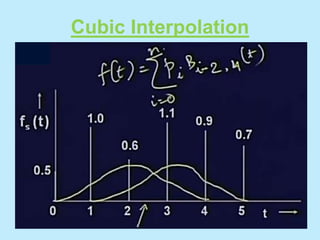
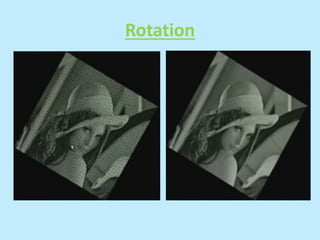
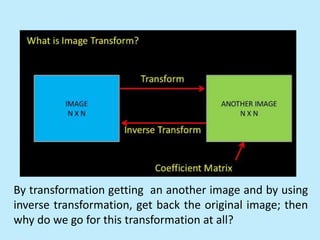
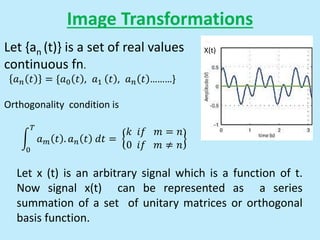
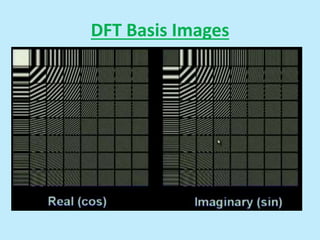
This document discusses image interpolation and resampling. It explains that interpolation is needed when transforming images, such as scaling or rotating, as the transformed coordinates are not usually integers. Various interpolation methods are covered, including constant, linear, and cubic interpolation using B-spline functions. Examples are provided to demonstrate cubic interpolation to estimate values between given sample points. The document also discusses properties of interpolation, such as using nearby sample values and avoiding discontinuities.

1. Digital Image
Processing
Dr. Rajib Kumar Jha
Associate Professor
Depart of Electrical Engineering
Indian Institute of Technology Patna
jharajib@iitp.ac.in
Lecture
Notes-2021
1

2. Lecture-7-8
Interpolation & Re-sampling
2

3. Contents
• Interpolation Operations
• When interpolation operations are needed
• B-Spline interpolations
3

4. Image Interpolation & Re-sampling
4
𝑆𝑥=3 & 𝑆𝑦=3
𝑥
𝑦 =
𝑆𝑥 0
0 𝑆𝑦
𝑥
𝑦
9 pixels are filled and
rest pixels are Unfilled,
showed by blue cross

5. Scaled Image
5

6. Image Interpolation & Re-sampling
(a) (b)
Transformed coordinates are not integers so
many transformed co-ordinates will be mapped
to one nearest integer co-ordinates.
𝑥 = 450
& y=450
0,0 → (0,0)
0,1 → (0.707,0.707)
0,2 → (1.414,1.414)
(1,0) → (0.707, −0.707)
1,1 → (1.414,0)
1,2 → (2.121,0.707)
(2,0) → (1.414, −1.414)
(2,1) → (2.121, −0.707)
2,2 → (2.828,0)

7. Rotated Image
7

8. Image Interpolation & Re-sampling
8
𝑆𝑥=3 & 𝑆𝑦=3
𝑥
𝑦 =
𝑆𝑥 0
0 𝑆𝑦
𝑥
𝑦
x=1/3 & y=1/3

9. Image Interpolation & Re-sampling
(a) (b)
Transformed coordinates are not integers so
many transformed co-ordinates will be mapped
to one nearest integer co-ordinates.
𝑥 = 450
& y=450
0,0 → (0,0)
0,1 → (0.707,0.707)
0,2 → (1.414,1.414)
(1,0) → (0.707, −0.707)
1,1 → (1.414,0)
1,2 → (2.121,0.707)
(2,0) → (1.414, −1.414)
(2,1) → (2.121, −0.707)
2,2 → (2.828,0)

10. Sampled Signal

11. Sampled Signal
1. We may need to find out the approximate value of these
functions at say t = 2.3 or say t = 3.7 and so on.
2. The purpose of image interpolation is by making use of the
sample values at distinct locations.
3. So, reconstruct the value of the function f(t) at any arbitrary
point in the time axis.

12. Properties of Interpolation

13. Properties
• I want to approximate the function value at locations
say t = 2.3, then the samples that should be
considered are the samples which are nearer to t =
2.3. We should not consider sample value at t = 50.
• we should not introduce any discontinuity in the
signal.
• Interpolation must be shift invariant. That is if we
shift the signal by say t = 5, even then the same
interpolation operation should give us the same
result in the same interval.

14. B-Spline Function
• B-Spline function is a piece wise polynomial
function that can be used to provide local
approximation of curves using very small number
of parameters.
• Because it is useful for local approximation of
curves so it can be very useful for smoothening
operation of some discrete curves,
• It is also very-very useful for interpolation of a
function from discrete number of samples.

15. B-Spline Function
15
So, this control points actually decide that how the B-spline
functions should be guided to give us a smooth curve.
Normalized B spline is Bi,k
of order k can be
recursively defined.
Pi is called control point
t
t
t
t
t
t
t
t
t
t t
t
t
t

16. B-Spline Function
𝐵0,1 t =
1 0 ≤ 𝑡 < 1
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
𝐵0,2 t =
𝑡 0 ≤ 𝑡 < 1
2 − 𝑡 1 ≤ 𝑡 < 2
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
𝐵0,3 t =
𝑡2
2
0 ≤ 𝑡 < 1
−𝑡2
+ 3𝑡 − 1.5 1 ≤ 𝑡 < 2
(3−𝑡)2
2
2 ≤ 𝑡 < 3
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

17. B-Spline Function
𝐵0,4 t =
𝑡3
6
0 ≤ 𝑡 < 1
−3𝑡3 + 12𝑡2 − 12𝑡 + 4
6
1 ≤ 𝑡 < 2
3𝑡3
− 24𝑡2
+ 60𝑡 − 44
6
2 ≤ 𝑡 < 3
(4 − 𝑡)3
6
3 ≤ 𝑡 < 4
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

18. Graphical Representation of B-Spline

19. Constant Interpolation

20. Constant Interpolation

21. Linear Interpolation
21

22. Linear Interpolation
22

23. Linear Interpolation

24. Modified interpolation Formula

25. Modified interpolation Formula
25

26. Modified interpolation Formula
26
Now with p0 we will consider B-spline from -0.5 to 0.5; for p1
B-spline function lie between 0.5 to 1.5 and so on.

27. B-spline Cubic interpolation function
27

28. Constant Interpolation

29. Constant Interpolation

30. Constant Interpolation

31. B-spline interpolation functions

32. Linear Interpolation

33. Cubic Interpolation

34. Example
• f(1)=1.5 Calculate f(4.3) ????
• f(2)=2.5 Given these sample values
• f(3)=3 Use Cubic interpolation
• f(4)=2.5
• f(5)=3
• f(6)=2.4
• f(7)=1
• F (8)=2.5

35. Example
𝑓 4.3 = 𝑓(3)𝐵1,4(4.3) + 𝑓(4)𝐵2,4(4.3) +
𝑓(5)𝐵3,4(4.3)+ 𝑓(6)𝐵4,4(4.3)
𝐵𝑖,𝑘 𝑡 = 𝐵0,𝑘(𝑡 − 𝑖)
= 𝑓(3)𝐵0,4(3.3) + 𝑓(4)𝐵0,4(2.3) +
𝑓 5 𝐵0,4 1.3 + 𝑓(6)𝐵0,4(0.3)
=2.7068 Constant interpolation=2.5
Linear Interpolation=2.65

36. Interpolation in Image

37. Scaling

38. Result

39. Rotation

40. Thanks
40

41. Contents
• Explain Image Transformation operations.
• Explain Unitary Transformations.
• Explain Orthogonal and Orthonormal basis vector.
• Explain how an arbitrary 1-D signal and
subsequently 2-D signal can be represented by
series summation of orthogonal basis vectors and
basis images.
• Computational Complexity of Image Transform
operation.
• Explain Separable Unitary Transformations.

42. By transformation getting an another image and by using
inverse transformation, get back the original image; then
why do we go for this transformation at all?

43. Image Transformations

44. The purpose of this image transformation operation is to
represent any arbitrary image as a series summation of such
unitary matrices or series summation of such basis images.

45. What is Unitary Transformation
• Discrete Fourier transform
coefficients or discrete cosine
transform coefficients, are different
types of unitary transformations.

46. Image Transformations
Let x (t) is an arbitrary signal which is a function of t.
Now signal x(t) can be represented as a series
summation of a set of unitary matrices or orthogonal
basis function.
Let {an (t)} is a set of real values
continuous fn.
𝑎𝑛 𝑡 = {𝑎0 𝑡 , 𝑎1 𝑡 , 𝑎𝑛 𝑡 ………}
Orthogonality condition is
0
𝑇
𝑎𝑚 𝑡 . 𝑎𝑛 𝑡 𝑑𝑡 =
𝑘 𝑖𝑓 𝑚 = 𝑛
0 𝑖𝑓 𝑚 ≠ 𝑛
X(t)

47. Image Transformation: An example
1. if I multiply sin(wt) with sin(3wt) and integrate, Similarly,
if I multiply sin(2wt) with sin(3wt) and integrate it will
be zero.
2. This particular set, sin(wt), sin(2wt), sin(3wt), is the set
of orthogonal basis functions.

48. Let x(t) is an arbitrary real values function.
This function x (t) can be represented by a series summation. So,
an (t) is the set of orthogonal basis functions.

49. by using that formula of orthogonality,

50. Properties of Basis function an(t)
an(t) is complete or closed if one of the two conditions hold.
1. There should be a signal x(t) having finite energy.
2. For any piecewise signal x(t), error energy should be
minimum.

51. • Let u(n) is a series of discrete samples represented in
the form of 1-D sequences. It has N samples
• For transformed vector v multiply u with
Transformation vector A. A is called unitary matrix of
size NxN
Discrete Sample Representation
u(n) : 0≤n≤ 𝑁 − 1
v = Au where
v is transformed vector and
A is Transformation vector

52. Unitary Matrix

53. 53

55. u(n) is represented as the series summation of set
of basis vector. If it has the property of orthogonal
then above condition holds.

56. Now, the same concept of representing a vector as a
series summation of a set of basis vectors can also
be extended in case of an image.

57. Here {ak,l (m,n) } is called an image transform; is a
set of complete orthogonal discrete basis functions
satisfying two properties ORTHOGONALITY AND
COMPLETENESS
Properties of image transform an(t)

59. Previous Discussion
u(n) is one dimensional discrete signal. In
matrix representation
This transformation is unitary transformation if

60. Previous Discussion
The original image can be obtained as u=A-1v. This
expression says that the input sequence u (n) is now
represented in the form of series summation of a set of
vectors or orthonormal basis vectors.

61. Previous Discussion-2D
Set of Complete orthonormal basis function

62. Reduce the computational complexity (N4)
is separable if and only if
Separable Unitary Transform property
=
{
{
This is complete orthogonal basis vectors

63. How this Separable Unitary Transform
helps in reducing the complexity
A =B

64. A has NxN size; U has NxN size ; So, Order of AU is
O(N3 ); Order of A is O(N3 ); Order of V is 2*O(N3 )

65. DFT Basis Images

66. DCT Basis Images

67. Example: A is orthogonal matrix & U is
input image; V=AUAT
Transformed Image

68. What is Basis Images

69. Thanks
69