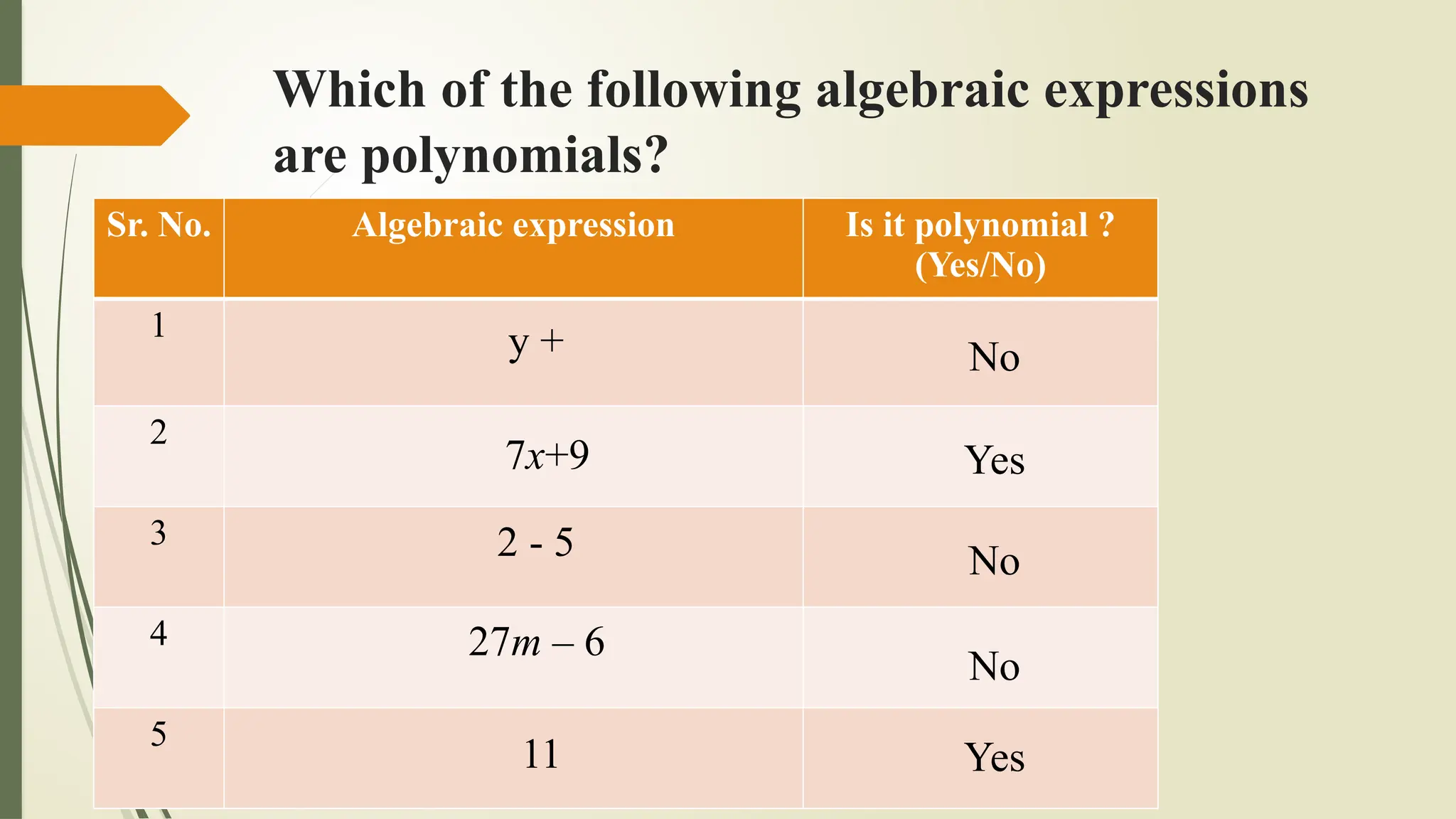
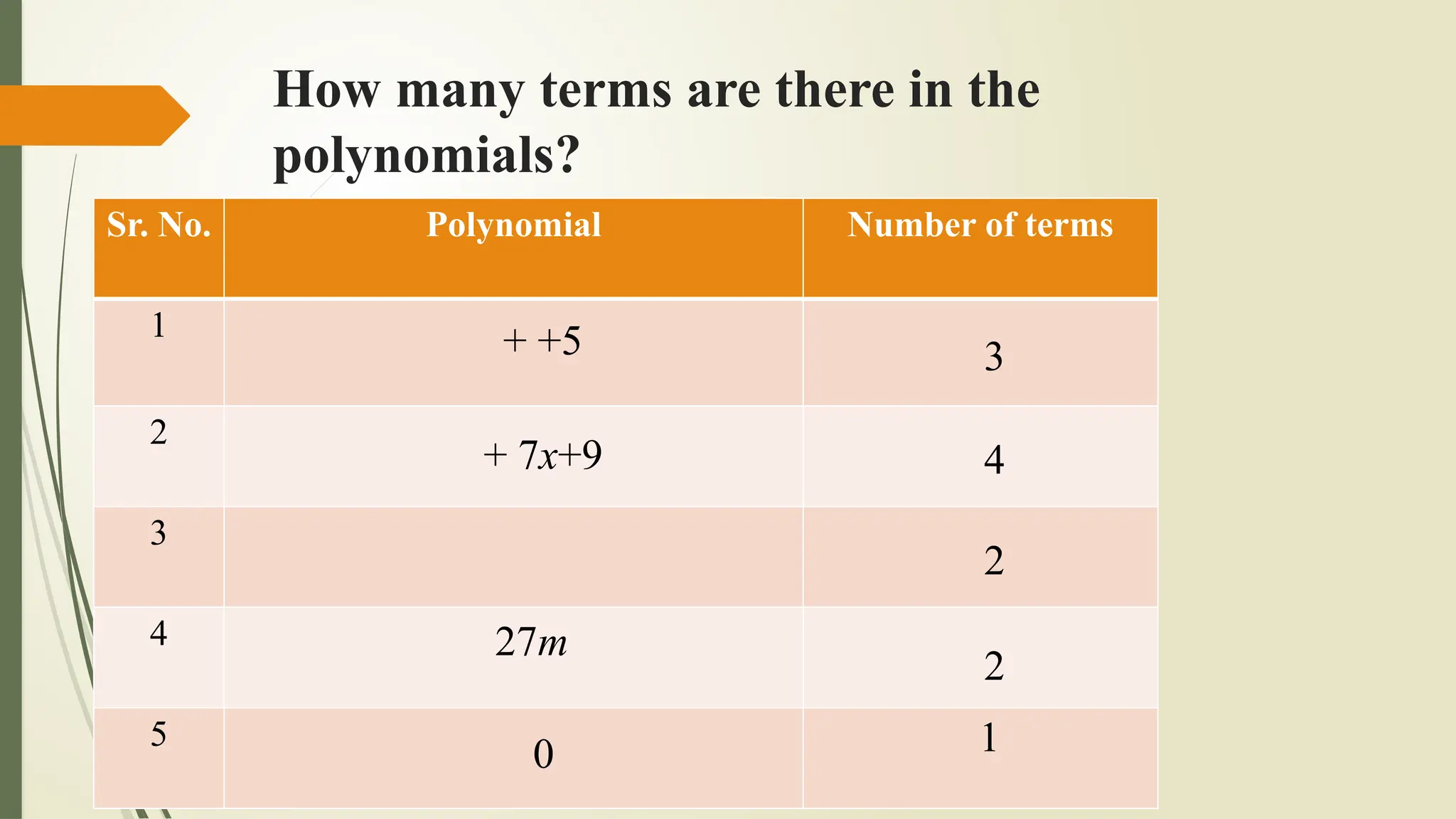
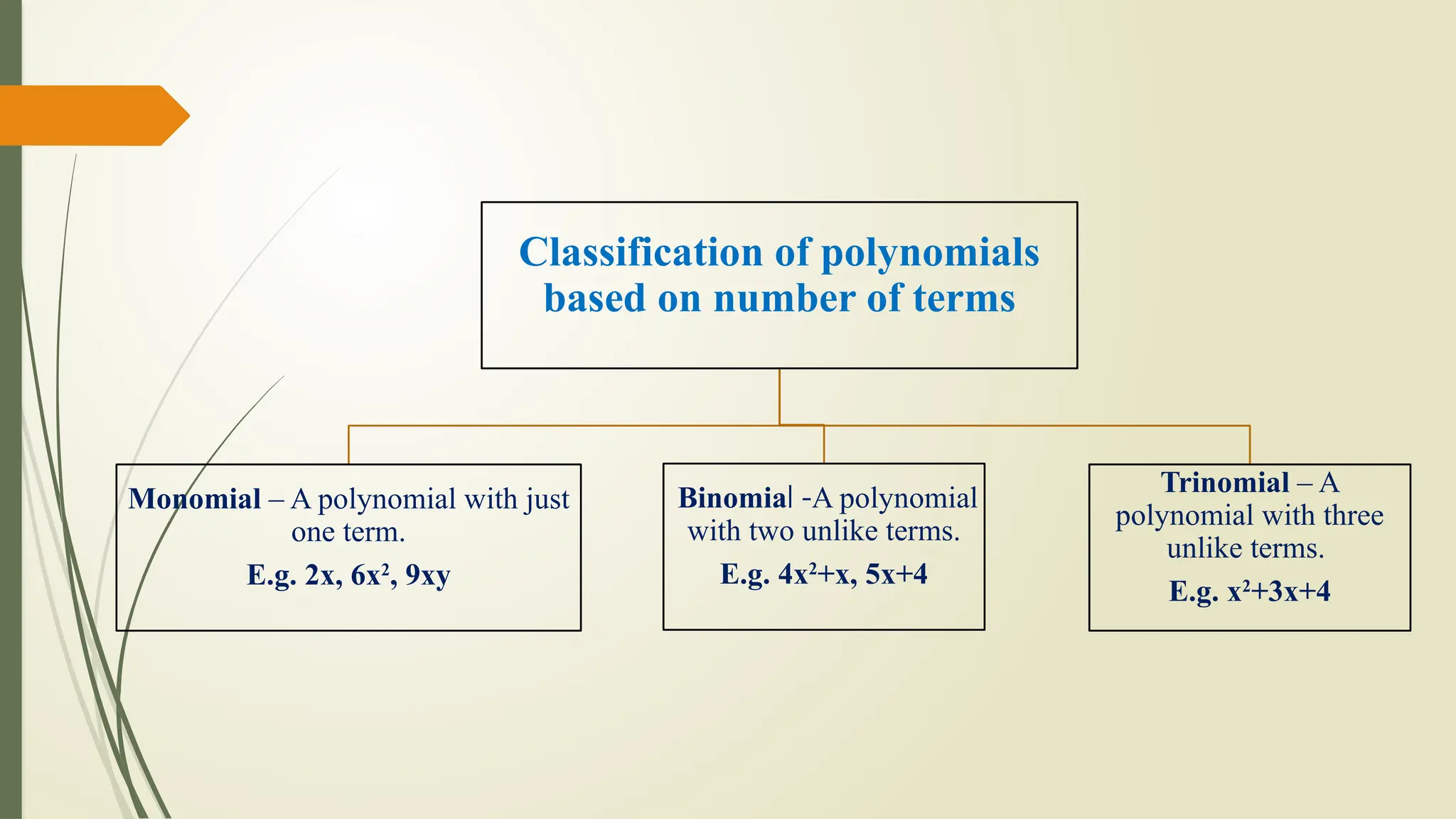
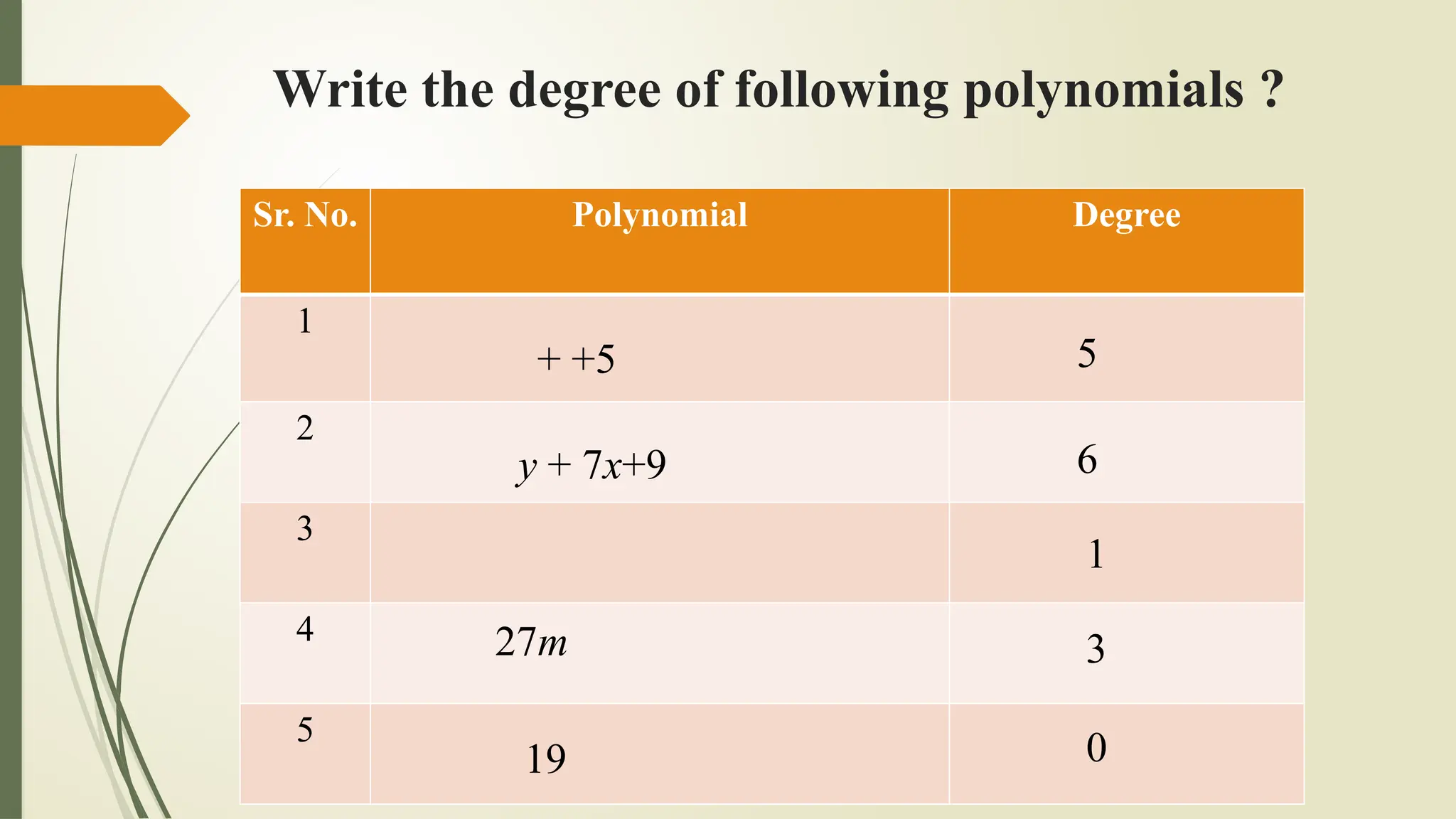
The document explains algebraic expressions, specifically defining polynomials as algebraic expressions with whole number exponents. It classifies polynomials based on the number of terms (monomial, binomial, trinomial) and degree (linear, quadratic, cubic). Examples illustrate the characteristics and classifications of polynomials.

1. Algebraic Expressions
An algebraic expression is an expression made up of
variables and constants along with mathematical
operators.
An expression or algebraic expression is any
mathematical statement which consists of numbers,
variables and an arithmetic operation between them.
E.g. x + 5y – 10 , 2x + 1, x + y

3. Polynomials
What is the meaning of word polynomial ?
The word polynomial is derived from the Greek words
‘poly’ means ‘many‘ and ‘nominal’ means ‘terms‘, so
altogether it is said as “many terms”

4. What is a Polynomial?
An algebraic expression, if the exponent /power of the
variables are whole numbers then that algebraic
expression is called as polynomial.
6, -8, , 0, etc. are constant numbers and called as
constant polynomials.
Remember that , power of variable should not be a fraction or
negative number.

5. Here, in this example, power of all variables is either 1 or 2 i.e.
whole number so given algebraic expression in a polynomial.

6. Which of the following algebraic expressions
are polynomials?
Sr. No. Algebraic expression Is it polynomial ?
(Yes/No)
1
2
3
4
5
y + No
7x+9
2 - 5
27m – 6
11
No
No
Yes
Yes

7. Classification of polynomials
We classify the polynomials mainly by two ways
1) Number of terms and
2) Degree of polynomial

8. Number of terms
6x4
+ 3x2
+ 5x +19 here in this polynomial there are
4 terms.

9. How many terms are there in the
polynomials?
Sr. No. Polynomial Number of terms
1
2
3
4
5 1
+ +5 3
+ 7x+9
27m
0
2
2
4

10. Classification of polynomials
based on number of terms
Monomial – A polynomial with just
one term.
E.g. 2x, 6x2
, 9xy
Binomial -A polynomial
with two unlike terms.
E.g. 4x2
+x, 5x+4
Trinomial – A
polynomial with three
unlike terms.
E.g. x2
+3x+4

11. Degree of a Polynomial
(when only one variable is present)
If given polynomial contain only one variable then its degree is
the highest power/ exponent of the variable in the given
polynomial.
e.g. 1) The degree of the polynomial x2
+ 2x+3 is 2,
as the highest power of x in the given expression is 2.
2) the degree of the polynomial x8
+ 2x6
– 3x + 9 is 8 ,
since the greatest power in the given expression is 8.

12. Note that,
Degree of any non -zero constant polynomial i.e. Any real number
except 0 is zero.
Why???
I can write any number let's say 5 as 5, here power of variable is 0 ,
∴ Degree is 0.
And such polynomials are called as constant polynomials.
0 is constat number and called as Zero polynomial .
Que. What is the degree of zero polynomial?
Not defined .

13. Degree of a Polynomial
(when more than one variable are present)
If given polynomial contains more than one variables, them its
degree is the highest sum of power of variables in each term of
the polynomial is the degree of polynomial.
e.g. 3 + 7 − mn , is a polynomial in two variables m and n.
Here
sum of power of variables in first terms (3) is 4+5 = 9
sum of power of variables in second terms (7 ) is 2+3 = 5
sum of power of variables in third terms (mn) is 1+1 = 2
∴ Degree of the given polynomial is 9

14. Write the degree of following polynomials ?
Sr. No. Polynomial Degree
1
2
3
4
5
+ +5 5
y + 7x+9
27m
19
1
3
6
0

15. Classification of polynomials
based on their degree
Linear Polynomial
A polynomial whose degree is one is
called a linear polynomial.
For example, 2x+1 is a linear
polynomial.
Quadratic Polynomial
A polynomial of degree two is
called a quadratic polynomial.
For example, 3x2
+8x+5 is a
quadratic polynomial.
Cubic Polynomial
A polynomial of degree three is
called a cubic polynomial.
For example, 2x3
+5x2
+9x+15 is
a cubic polynomial.

16. Thank you