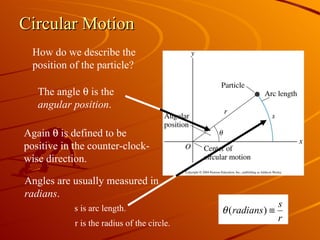
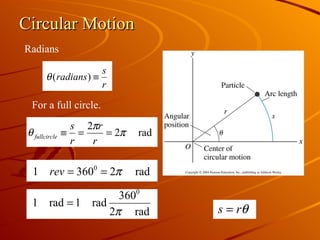
The document discusses uniform circular motion and related concepts. It describes uniform circular motion as a particle moving at constant speed in a circle. It also discusses angular position, angular velocity, centripetal acceleration, coordinate systems used to analyze circular motion, and problem-solving strategies for circular motion problems.

1. Circular Motion Kinematics of Uniform Circular Motion (Description of Uniform Circular Motion) Dynamics of Uniform Circular Motion (Why does a particle move in a circle?)

2. Reading Question Reviewing for the exam I have spent Zero hours ½ hour 1 hour 1 ½ hours 2 hours 2 ½ hours 3 or more hours

3. Reading Question 1. x - and y -axes. 2. x -, y -, and z -axes. 3. x - and z -axes. 4. r -, t -, and z -axes. Circular motion is best analyzed in a coordinate system with

4. Reading Question 1. x - and y -axes. 2. x -, y -, and z -axes. 3. x - and z -axes. 4. r -, t -, and z -axes. Circular motion is best analyzed in a coordinate system with

5. Reading Question 1. the circular weight. 2. the angular velocity. 3. the circular velocity. 4. the centripetal acceleration. The quantity with the symbol  is called

6. Reading Question 1. the circular weight. 2. the angular velocity. 3. the circular velocity. 4. the centripetal acceleration. The quantity with the symbol  is called

7. Reading Question 1. points toward the center of the circle. 2. points toward the outside of the circle. 3. is tangent to the circle. 4. is zero. For uniform circular motion, the net force

8. Reading Question 1. points toward the center of the circle. 2. points toward the outside of the circle. 3. is tangent to the circle. 4. is zero. For uniform circular motion, the net force

9. Circular Motion Uniform circular motion is a particle moving at constant speed in a circle.

10. Circular Motion Is the velocity changing? Yes, changing in direction but not in magnitude. Is the speed changing? The period is defined as the time to make one complete revolution

11. Circular Motion The angle  is the angular position . How do we describe the position of the particle? Again  is defined to be positive in the counter-clock-wise direction. Angles are usually measured in radians . s is arc length. r is the radius of the circle.

12. Circular Motion Radians For a full circle.

13. Circular Motion Angular velocity We will worry about the direction later. Like one dimensional motion +- will do. Positive angular velocity is counter-clock=wise. The angular displacement is Average angular velocity Instantaneous angular velocity

14. Circular Motion Coordinate System

15. Circular Motion So, is there an acceleration?

16. Circular Motion So, is there an acceleration?

17. Student Workbook

18. Student Workbook

19. Student Workbook

20. Student Workbook

21. Student Workbook side of plane Which way is the plane turning? To the left

22. Circular Motion So, is there an acceleration? Yes directed toward the center of curvature (center of circle)

23. Class Questions A particle moves cw around a circle at constant speed for 2.0 s. It then reverses direction and moves ccw at half the original speed until it has traveled through the same angle. Which is the particle’s angle-versus-time graph? 1. 2. 3. 4.

24. Class Questions A particle moves cw around a circle at constant speed for 2.0 s. It then reverses direction and moves ccw at half the original speed until it has traveled through the same angle. Which is the particle’s angle-versus-time graph? 1. 2. 3. 4.

25. Class Questions 1. ( a r ) b > ( a r ) e > ( a r ) a > ( a r ) d > ( a r ) c 2. ( a r ) b = ( a r ) e > ( a r ) a = ( a r ) c > ( a r ) d 3. ( a r ) b > ( a r ) a = ( a r ) c = ( a r ) e > ( a r ) d 4. ( a r ) b > ( a r ) a = ( a r ) a > ( a r ) e > ( a r ) d 5. ( a r ) b > ( a r ) e > ( a r ) a = ( a r ) c > ( a r ) d Rank in order, from largest to smallest, the centripetal accelerations ( a r ) a to ( a r ) e of particles a to e. 1. 2. 3. 4. 5.

26. Class Questions 1. ( a r ) b > ( a r ) e > ( a r ) a > ( a r ) d > ( a r ) c 2. ( a r ) b = ( a r ) e > ( a r ) a = ( a r ) c > ( a r ) d 3. ( a r ) b > ( a r ) a = ( a r ) c = ( a r ) e > ( a r ) d 4. ( a r ) b > ( a r ) a = ( a r ) a > ( a r ) e > ( a r ) d 5. ( a r ) b > ( a r ) e > ( a r ) a = ( a r ) c > ( a r ) d Rank in order, from largest to smallest, the centripetal accelerations ( a r ) a to ( a r ) e of particles a to e. 1. 2. 3. 4. 5.

27. Circular Motion

28. Circular Motion PROBLEM-SOLVING STRATEGY 7.1 Circular motion problems MODEL Make simplifying assumptions. VISUALIZE Pictorial representation. Establish a coordinate system with the r -axis pointing toward the center of the circle. Show important points in the motion on a sketch. Define symbols and identify what the problem is trying to find. Physical representation. Identify the forces and show them on a free-body diagram. SOLVE Newton’s second law is . Determine the force components from the free-body diagram. Be careful with signs. . SOLVE for the acceleration, then use kinematics to find velocities and positions. ASSESS Check that your result has the correct units, is reasonable, and answers the questions.