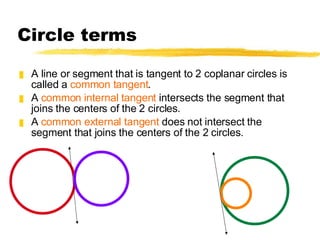
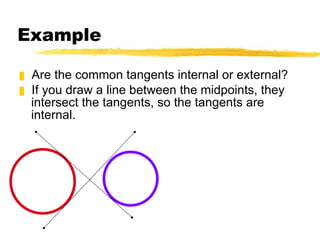
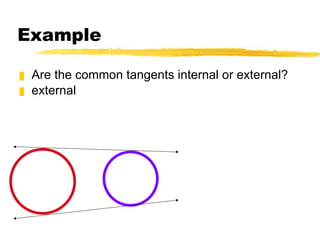
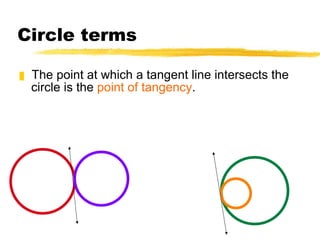
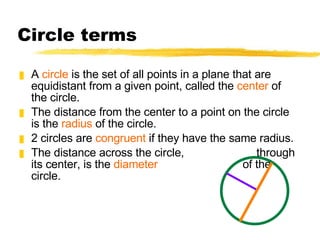
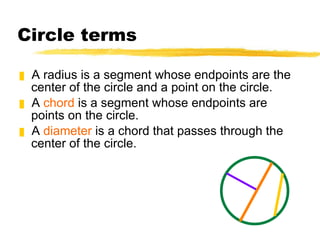
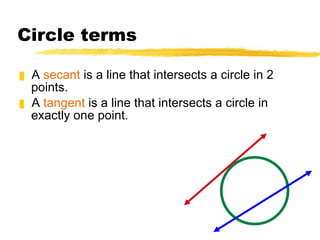
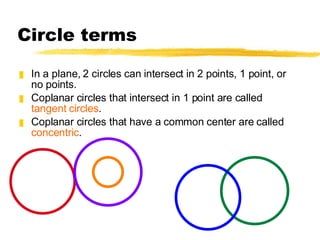
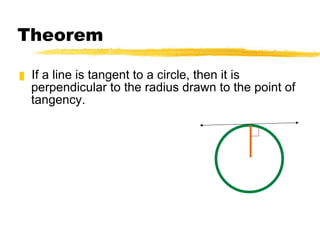
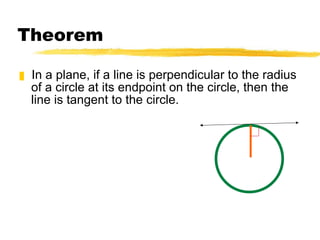
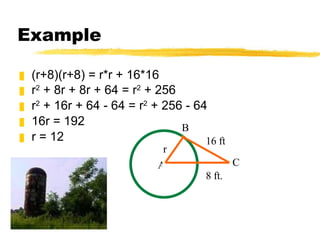
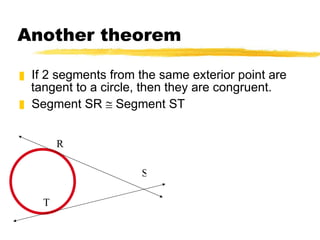
The document discusses key terms and theorems related to circles, including: - Definitions of circles, radii, diameters, chords, secants, tangents - Types of circle intersections and relationships (concentric, tangent) - Theorems about tangents being perpendicular to radii and lines perpendicular to radii being tangents - Using properties of tangents, radii, and perpendicular lines to solve problems about circles - The Pythagorean theorem can be used with right triangles formed with radii and tangent segments

1. Chapter 10 - Circles Objectives: Use arcs, angles, & segments in circles to solve problems Use the graph of an equation of a circle to model problems

2. 10.1 Tangents to Circles Objectives: Identify segments and lines related to circles Use tangents to solve problems

3. Circle terms A circle is the set of all points in a plane that are equidistant from a given point, called the center of the circle. The distance from the center to a point on the circle is the radius of the circle. 2 circles are congruent if they have the same radius. The distance across the circle, through its center, is the diameter of the circle.

4. Circle terms A radius is a segment whose endpoints are the center of the circle and a point on the circle. A chord is a segment whose endpoints are points on the circle. A diameter is a chord that passes through the center of the circle.

5. Circle terms A secant is a line that intersects a circle in 2 points. A tangent is a line that intersects a circle in exactly one point.

6. Circle terms In a plane, 2 circles can intersect in 2 points, 1 point, or no points. Coplanar circles that intersect in 1 point are called tangent circles . Coplanar circles that have a common center are called concentric .

7. Circle terms A line or segment that is tangent to 2 coplanar circles is called a common tangent . A common internal tangent intersects the segment that joins the centers of the 2 circles. A common external tangent does not intersect the segment that joins the centers of the 2 circles.

8. Example Are the common tangents internal or external? If you draw a line between the midpoints, they intersect the tangents, so the tangents are internal.

9. Example Are the common tangents internal or external? external

10. Example Look at the picture on the bottom of page 596. What is the center of Circle A? 4,4 What is the center of Circle B? 5,4 What is the point of intersection? 8,4 What is the common tangent? The line x = 8

11. Circle terms The point at which a tangent line intersects the circle is the point of tangency .

12. Theorem If a line is tangent to a circle, then it is perpendicular to the radius drawn to the point of tangency.

13. Theorem In a plane, if a line is perpendicular to the radius of a circle at its endpoint on the circle, then the line is tangent to the circle.

14. Example You are standing 8 feet from a grain silo. The distance from you to a point of tangency on the tank is 16 feet. What is the radius of the silo? r 16 ft 8 ft. B A C

15. Example How do we know B is a right angle? How do we know side AC is r + 8 feet? Can we use the Pythagorean Theorem now? r 16 ft 8 ft. B A C

16. Example (r+8)(r+8) = r*r + 16*16 r 2 + 8r + 8r + 64 = r 2 + 256 r 2 + 16r + 64 - 64 = r 2 + 256 - 64 16r = 192 r = 12 r 16 ft 8 ft. B A C

17. Another theorem If 2 segments from the same exterior point are tangent to a circle, then they are congruent. Segment SR  Segment ST S R T

18. Homework Do worksheets