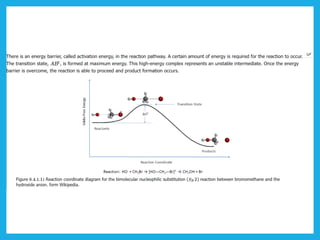
Chemical dynamics is a branch of physical chemistry that examines the rates and mechanisms of reactions, focusing on energy transfer at atomic scales. Key concepts include the Arrhenius equation, activation energy, and kinetic theories that describe how temperature and catalysts influence reaction rates. Additionally, the document covers chain reactions, steady-state kinetics, and the effects of ionic strength on reaction rates in solutions.

1. Chemical Dynamics is a field within physical chemistry that focuses on
the study of the rates and mechanisms of chemical reactions. It also
involves understanding how energy is transferred among molecules as
they undergo collisions in gas-phase or condensed-phase environments.
This field is closely related to chemical kinetics, but it goes a step further
by focusing on individual chemical events on atomic length scales and
over very brief time periods. The experimental and theoretical tools
used in chemical dynamics must be capable of monitoring the chemical
identity and energy content (i.e., electronic, vibrational, and rotational
state populations) of the reacting species.
Moreover, because the rates of chemical reactions and energy transfer
are of utmost importance, these tools must be capable of doing so on
time scales over which these processes, which are often very fast, take
place.

2. Microscopic Kinetics, on the other hand, is concerned with the
behavior of individual molecules during a reaction. It involves
understanding how molecules interact with each other, how often
these interactions (or collisions) occur, and what happens during
these interactions.
Macroscopic Kinetics - refers to the study of reaction rates on a scale
that we can observe directly. It involves measuring the rate at which
a reaction occurs and how this rate changes under different
conditions. For example, if we are observing a chemical reaction in a
beaker, we might measure the rate at which the reactants are
consumed or the products are formed.

15. Arrhenius Equation
The Arrhenius equation is a mathematical expression that describes the
temperature dependence of reaction rates. It was proposed by Swedish
chemist Svante Arrhenius in 1889. Here are its key characteristics:
1. Expression: The equation is expressed as `k = Ae^(-Ea/RT)`, where:
- `k` is the rate constant of the reaction.
- `A` is the pre-exponential factor, which can be visualized as the frequency
of correctly oriented collisions between reactant particles.
- `Ea` is the activation energy of the chemical reaction.
- `R` is the universal gas constant.
- `T` is the absolute temperature associated with the reaction (in Kelvin).
2. Temperature Dependence: The equation provides insight into the
dependence of reaction rates on the absolute temperature. As activation
energy term `Ea` increases, the rate constant `k` decreases and therefore the
rate of reaction decreases.

16. 3. Arrhenius Plot: When logarithms are taken on both sides of the equation, it
can be written in a form that corresponds to that of a straight line (y = mx + c).
When the logarithm of the rate constant (`ln K`) is plotted on the Y-axis and the
inverse of the absolute temperature (`1/T`) is plotted on the X-axis, the resulting
graph is called an Arrhenius plot.
4. Catalysts: The function of a catalyst is to lower the activation energy
required by a reaction. Therefore, the lowered activation energy (accounted by
the catalyst) can be substituted into the Arrhenius equation in order to obtain
the rate constant for the catalysed reaction.
5. Pre-exponential Factor: Arrhenius originally considered `A` to be a
temperature-independent constant for each chemical reaction. However, more
recent treatments include some temperature dependence.
The Arrhenius equation has a vast and important application in determining the
rate of chemical reactions and for calculation of energy of activation.

17. Activation Energy
The energy of activation is a crucial concept in the field of chemical
kinetics. Here are some of its significant aspects:
 Definition: Activation energy is defined as the minimum amount
of extra energy required by a reacting molecule to get converted
into a product. It can also be described as the minimum amount of
energy needed to activate or energise molecules or atoms so that
they can undergo a chemical reaction or transformation.
 Reaction Rate: The activation energy of a chemical reaction is
closely related to its rate. Specifically, the higher the activation
energy, the slower the chemical reaction will be. This is because
molecules can only complete the reaction once they have reached
the top of the activation energy barrier.

18.  Nature of Reactants: The value of activation energy depends on
the nature of reactants. For ionic reactants, the value will be low
because there is an attraction between reacting species. While in
the case of covalent reactants, the value will be high because
energy is required to break the older bonds.
 Catalysts: A catalyst is a substance that either increases or
decreases the rate of a chemical reaction. In terms of activation
energy, a catalyst lowers it, making it easier for a reaction to occur.
However, the energies of the original reactants remain the same.
 Temperature Independence: Activation energy does not depend
upon temperature, pressure, volume, concentration, or
coefficients of reactant.

19. Temperature Co-efficient
The temperature coefficient describes the relative change of a physical property
that is associated with a given change in temperature.
For a property R that changes when the temperature changes by dT, the
temperature coefficient α is defined by the following equation
α=(1/R) (dR/dT)
Here, α has the dimension of an inverse temperature and can be expressed e.g. in
1/K or K−1. If the temperature coefficient itself does not vary too much with
temperature, a linear approximation will be useful in estimating the value R of a
property at a temperature T, given its value R0 at a reference temperature T0.In
terms of electrical resistance, the temperature coefficient of resistance is generally
defined as the change in electrical resistance of a substance with respect to per
degree change in temperature. So if we look at the electrical resistance of
conductors such as gold, aluminium, silver, copper, etc., it all depends upon the
process of collision between the electrons within the material. When the
temperature increases, the process of electron collision becomes rapid and faster.
As a result, the resistance will increase with the rise in temperature of the
conductor.

20. The relation between temperature and resistances R0 and RT is
approximately given as:
RT=R0[1+α(T−T0)]
Hence, it is clear from the above equation that the change in
electrical resistance of any substance due to temperature depends
mainly on three factors:
• The value of resistance at an initial temperature.
• The rise in temperature.
• The temperature coefficient of resistance α.
The value of α can vary depending on the type of material.

21. Thermodynamical formulation of reaction rates (Wynne-Jones and
Eyring treatment)

26. Reaction between ions in solutions - Influence of ionic strength on
reaction rates
When ions are in solution, they are pulled apart by the dissolving
properties of water. For example, when salt (NaCl) dissolves in water,
ions of sodium and chloride pull away from each other. Many
reactions take place between dissolved ions. For instance, halide ions
will react with silver nitrate (AgNO3) to give colored precipitates of
silver halides.
The rate of reaction in the case of ionic reactions is strongly
dependent upon the nature of the solvent used and the ionic
strength. The influence of electrolyte concentration on the rate
constants of a number of reactions involving ions in aqueous
solutions can be explained in terms of transition state theory and the
Debye-Hückel theory.

27. Primary Salt Effect and Secondary Salt Effect
The primary salt effect refers to how the concentration of electrolyte
affects the activity coefficient and consequently the rate of reaction.
This effect is profound when the reaction takes place between ions,
even at low concentrations.
On the other hand, the secondary salt effect is used to indicate a
kinetic salt effect due to a change in concentration of the reacting
ions on account of a change in the inter-ionic forces. If the addition of
electrolytes changes the actual concentration of reacting ions, then
such an effect is known as a secondary kinetic salt effect.
Both primary and secondary salt effects are important in the study of
ionic reactions in solutions.

28. Concept of Steady state kinetics-
In chemical kinetics, a steady state refers to a condition where all the
state variables remain constant or change negligibly despite ongoing
processes trying to change them. For any reaction to successfully
occur, it is imperative to study the involvement of free energy
changes in a reaction.
The steady-state approximation, occasionally called the stationary-
state approximation or Bodenstein’s quasi-steady-state
approximation, involves setting the rate of change of a reaction
intermediate in a reaction mechanism equal to zero so that the
kinetic equations can be simplified by setting the rate of formation of
the intermediate equal to the rate of its destruction.

29. In practice, it is sufficient that the rates of formation and destruction are
approximately equal, which means that the net rate of variation of the
concentration of the intermediate is small compared to the formation and
destruction, and the concentration of the intermediate varies only slowly, similar
to the reactants and products.
In a prototypical experiment, an enzyme reaction is initiated by the combination
of free enzyme and substrate rather instantly compared to the other things that
happen. The period immediately after the initiation is characterized by the
increase in concentration of the downstream intermediates of the reaction and
is called the pre-steady-state period. The pre-steady-state period is followed by a
second period during which these intermediates of the reaction are in relatively
constant concentration. During this latter period, called the steady-state period,
the rate of appearance of product is most nearly constant. This is called the
initial velocity of the reaction.
It theoretically takes an infinite time to reach steady state, just as it takes an
infinite time to reach chemical equilibrium. Both concepts are, however,
frequently used approximations because of the substantial mathematical
simplifications these concepts offer.

30. Chain reactions - chain length and chain inhibition
A chain reaction is a sequence of reactions where a reactive product
or by-product causes additional reactions to take place. In a chain
reaction, positive feedback leads to a self-amplifying chain of events.
Chain reactions are one way that systems which are not in
thermodynamic equilibrium can release energy or increase entropy
in order to reach a state of higher entropy.
Examples include-
• Polymerase Chain Reaction: The real-time polymerase chain
reaction (PCR) is a technique that makes a million copies of the
DNA, allowing scientists to use it for genetic research, forensic
analysis, and medical diagnosis.

31. • Nuclear Chain Reaction: The nuclear chain reaction is a series of
chemical reactions where a nucleus, typically 235 U, is bombarded
with neutrons, thereby creating an explosion and releasing a large
amount of energy. This process is also known as nuclear fission
and is the principle behind the first atom bomb developed in the
1940s.
• Chlorination of Ethane: If we mix chlorine (Cl2) and ethane
(CH3CH3) together at room temperature, there is no detectable
reaction3. However, if we shine light on the mixture or heat it, a
reaction occurs that substitutes chlorine atoms for hydrogen
atoms in ethane. This reaction proceeds via a chain mechanism.
In each of these examples, the products generated in a single
reaction cycle become the reactants to initiate the next reaction. A
chain reaction can be self-sustaining or controlled. The reaction will
continue until the system reaches a stable state.

32. The chain length in a chain reaction is defined as the average number of
times that the closed cycle of chain propagation steps is repeated. It is
equal to the rate of the overall reaction divided by the rate of the
initiation step in which the chain carriers are formed.
Chain inhibition refers to the elementary steps in a chain reaction that do
not lead to the formation of new products. These steps prevent the chain
propagation reaction. Addition of other materials in the reaction mixture
can lead to the inhibition reaction.
Chain inhibition is particularly important in controlling reactions that
could otherwise lead to explosive increases in reaction rates, and indeed
to chemical explosions themselves. For example, in the chlorination of
methane, light or heat can cause a chlorine molecule to split into two
chlorine atoms, which are very reactive. These atoms can react with
methane to form chloromethane and a hydrogen atom. The hydrogen
atom can then react with another chlorine molecule to form hydrogen
chloride and another chlorine atom. This chain reaction can continue
until all the methane or chlorine is used up.

33. However, if oxygen is present, it can react with the chlorine atoms to
form chlorine monoxide. This prevents the chlorine atoms from
reacting with methane, effectively inhibiting the chain reaction.

34. Comparision between Photochemical and Thermal reactions -