![Computing the Geometric or
Compound Average Rate of Return
Arithmetic Average = (40-50) ÷ 2 =
-5%
Geometric Average
= [(1+Ryear1) × (1+Ryear 2)]1/2 - 1
= [(1.4) × (.5)] 1/2 - 1
= -16.33%](https://image.slidesharecdn.com/chapter7-anintroductiontoriskandreturn-140220131248-phpapp02/75/Chapter7-an-introduction-to-risk-and-return-40-2048.jpg)
Uploaded byRodel Falculan
Chapter7 an introduction to risk and return
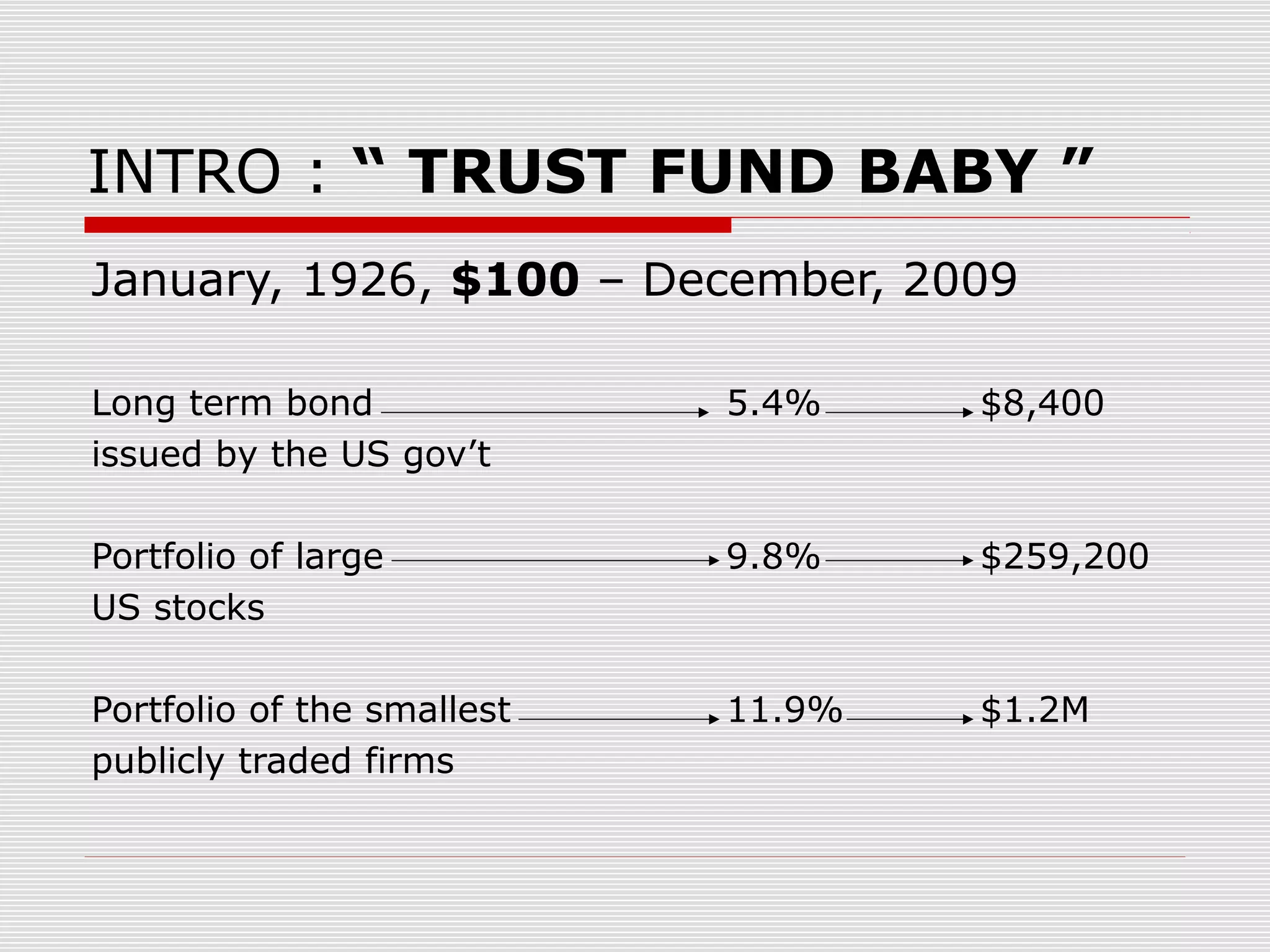
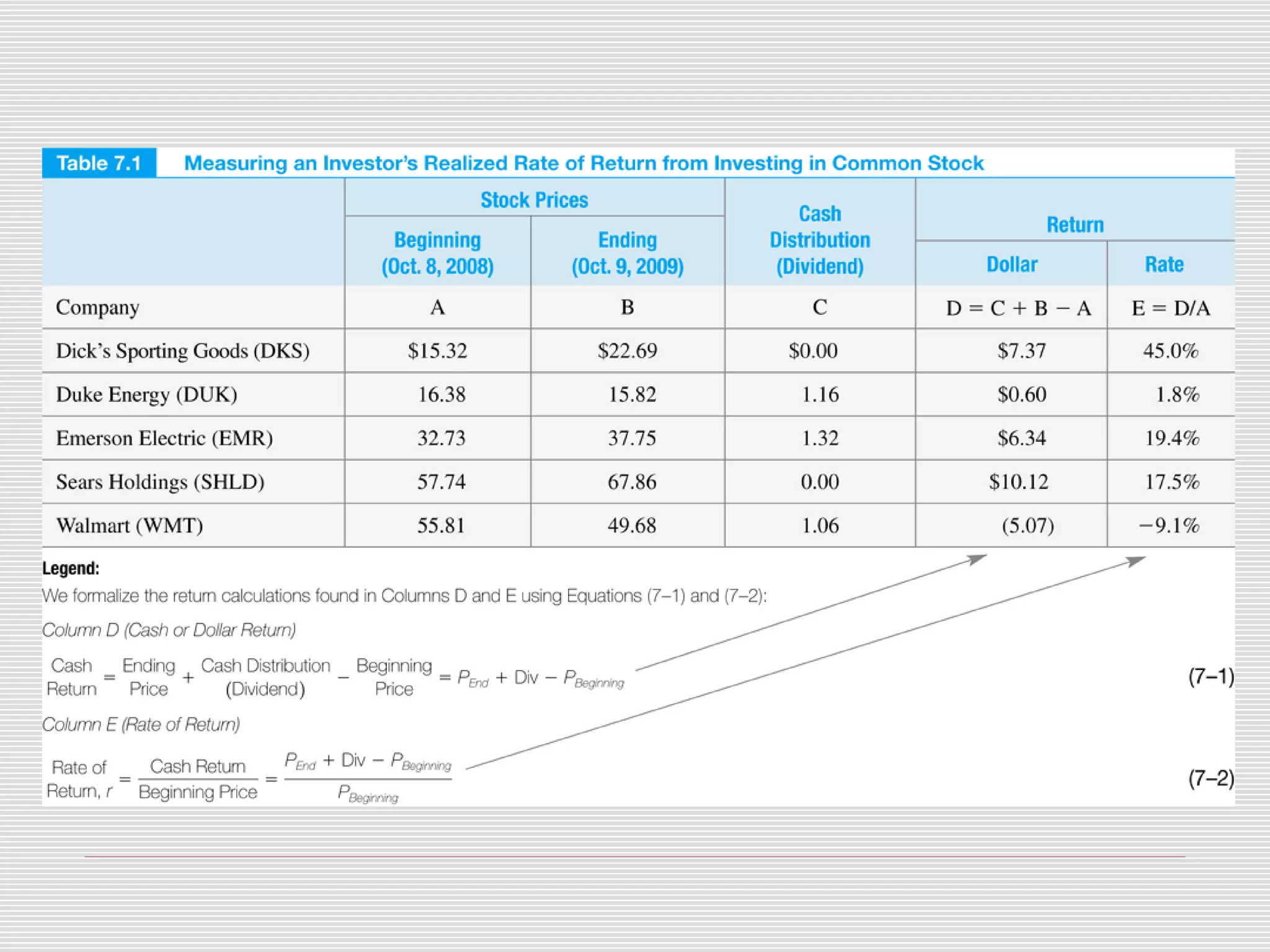
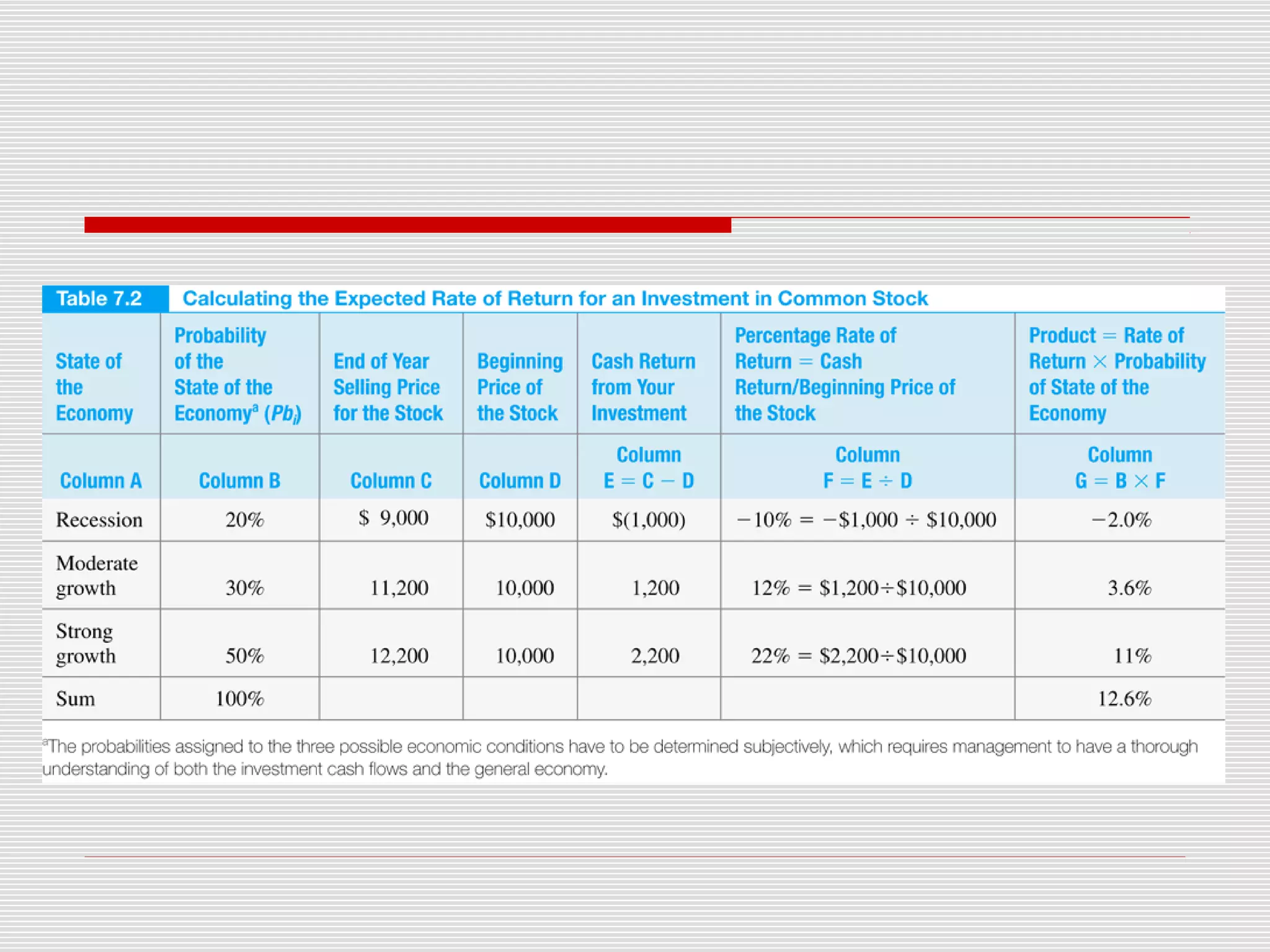
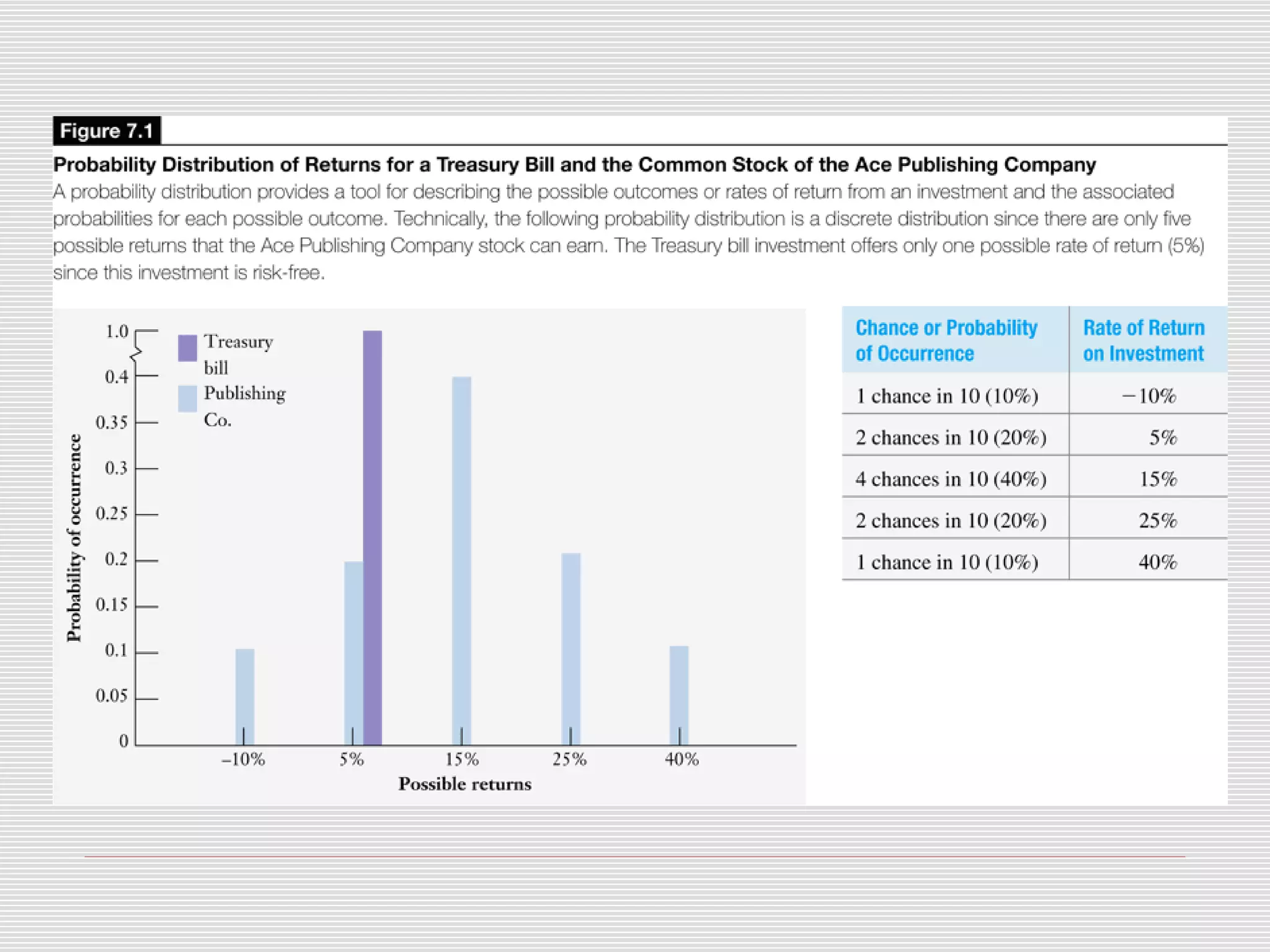
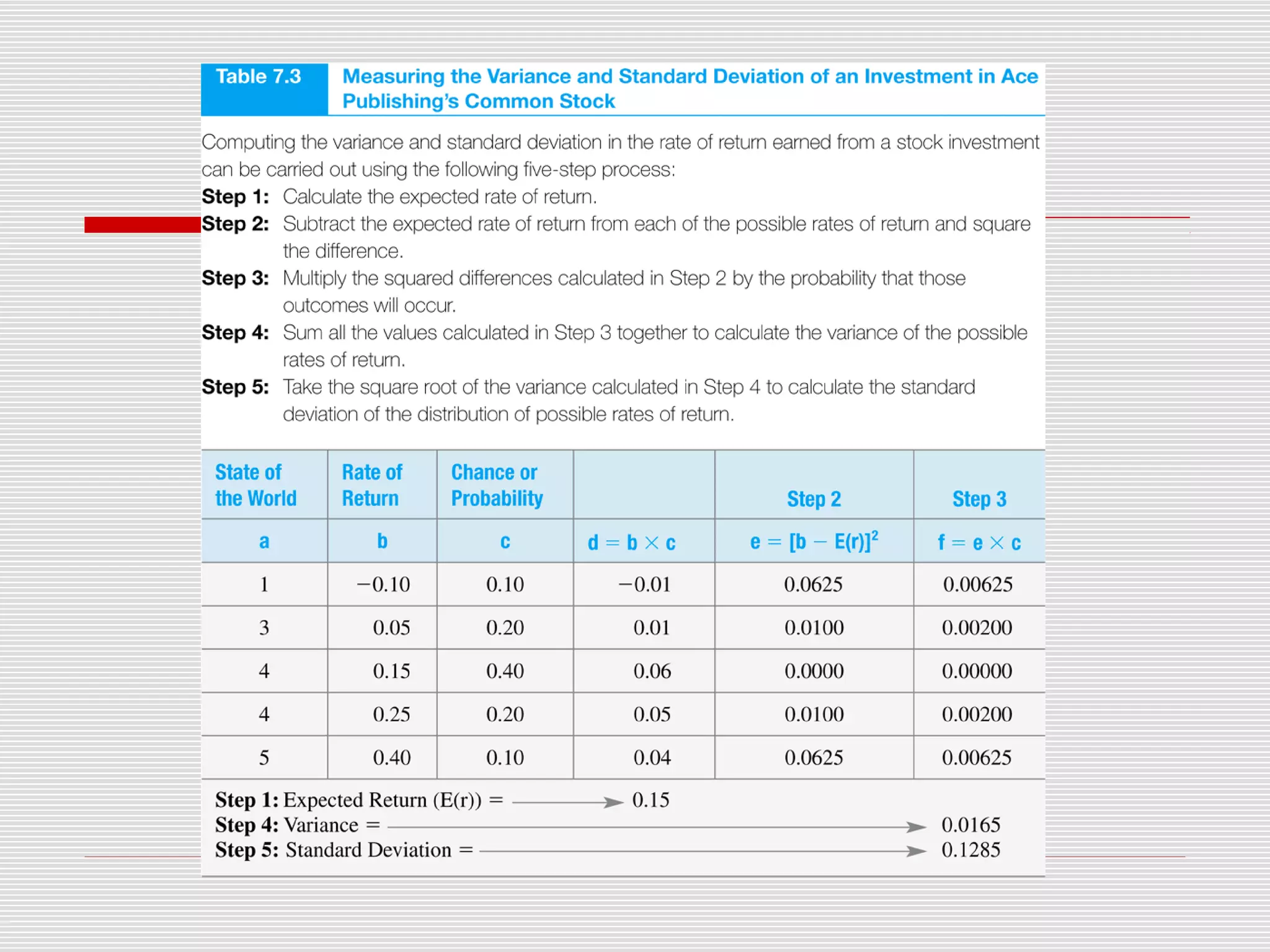
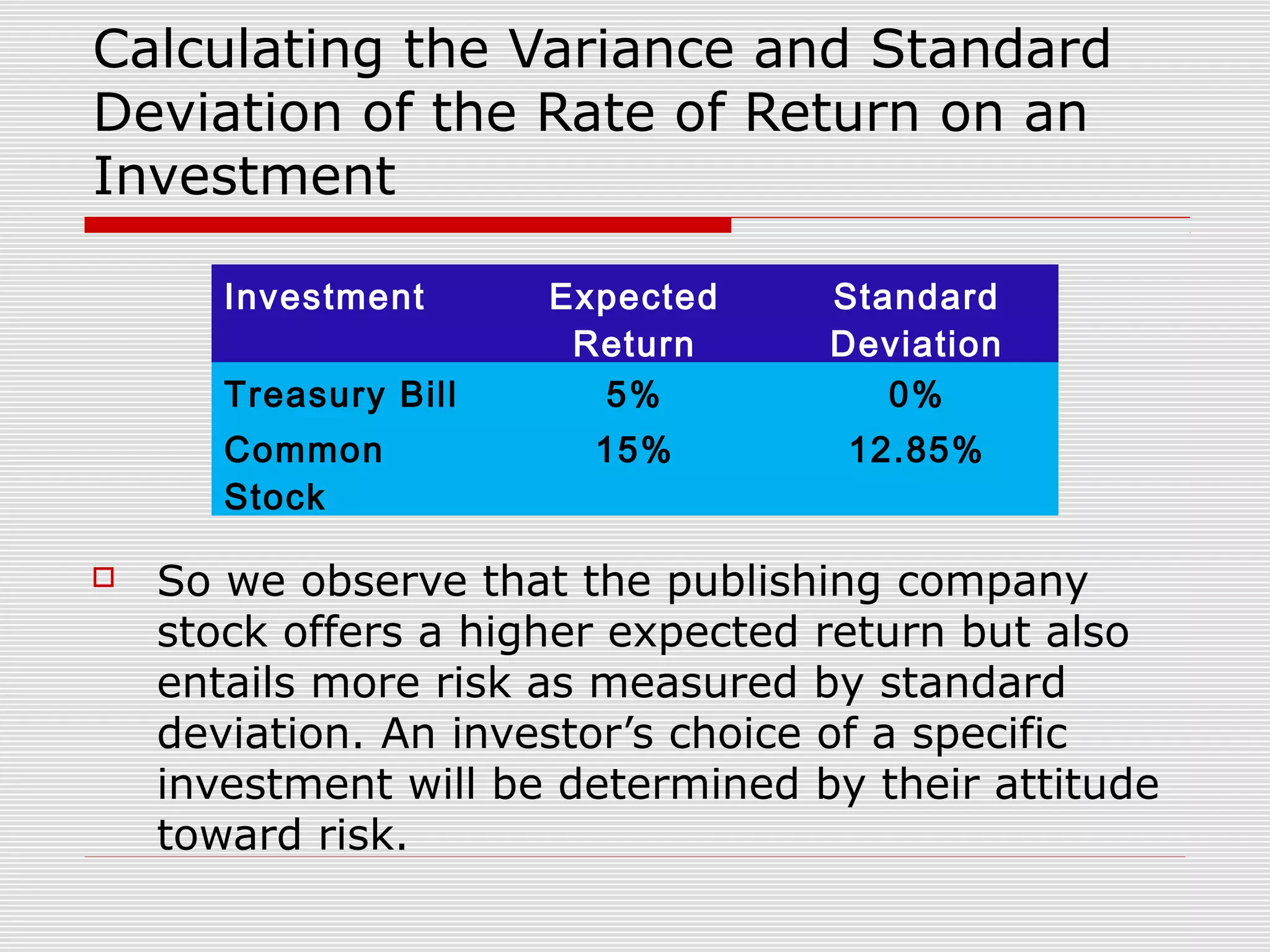
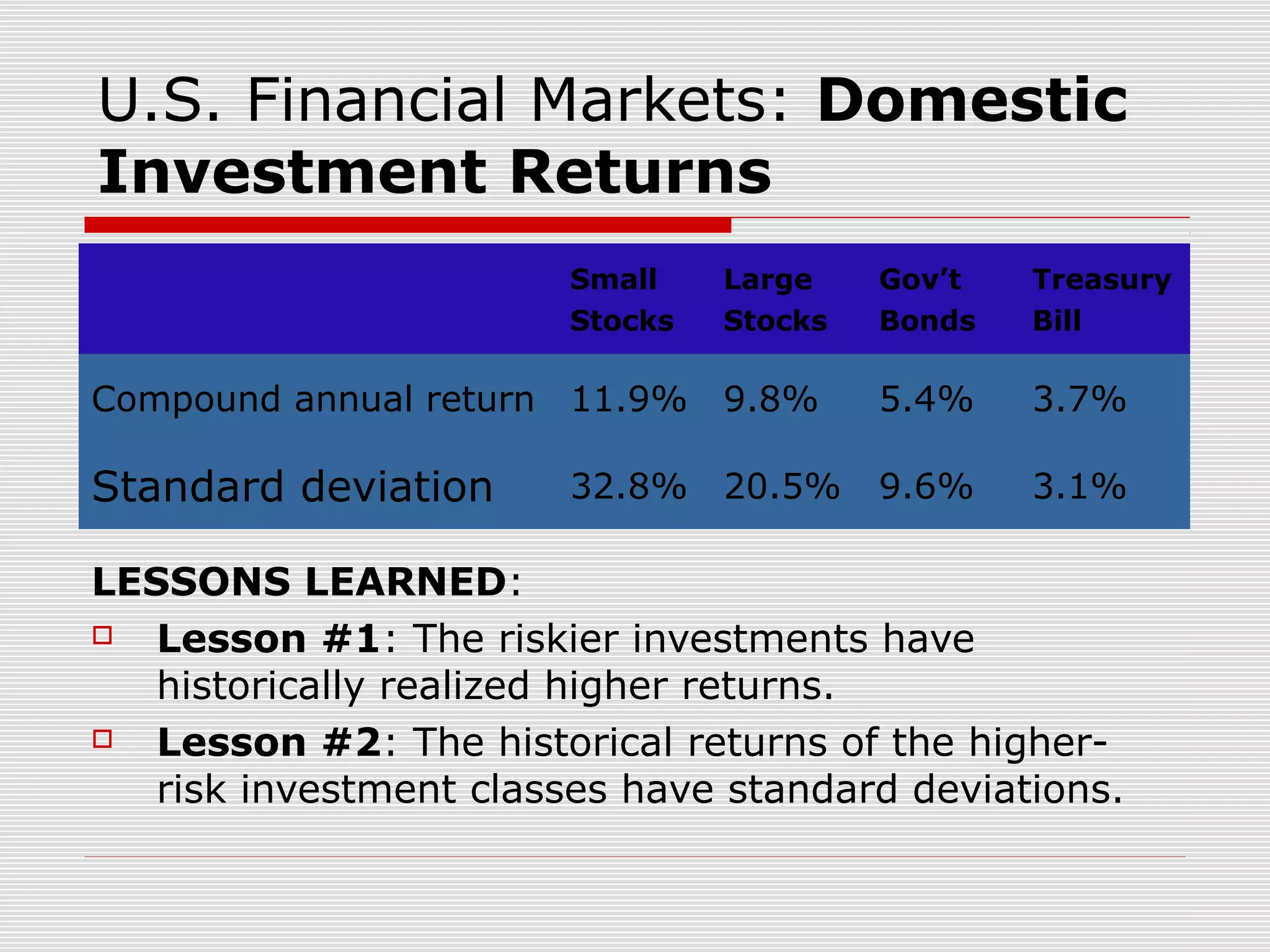
This chapter discusses risk and return in financial markets. It defines realized and expected rates of return as well as risk. Historically, riskier investments like small stocks have achieved higher average returns than less risky investments like government bonds, but also experienced greater price fluctuations. The chapter compares arithmetic and geometric average returns and explains why the geometric average best measures the compound growth rate. The efficient market hypothesis posits that market prices instantly reflect all available information.
More Related Content
Similar to Chapter7 an introduction to risk and return
Chapter7 an introduction to risk and return
- 1. CHAPTER 7 An Introductionto Risk and Return History of Financial Market Returns Rodel F. Falculan
- 2. Chapter Outline Realized andExpected Rates of Return & Risk Objective. A Brief History of Financial Market Returns Objective. Geometric vs. Arithmetic Average Rates of Return Objective. What Determines Stock Prices? Objective. Calculate realized & expected rates of return & risk. Describe the historical pattern of financial market returns. Compute geometric & arithmetic average rates of return. Explain the efficient market hypothesis and why it is important to stock market.
- 3. Principles Applied Principle 2: There Is a Risk-Return Tradeoff “investing in higher risk investments does not always result in higher realized rates of return ( that’s why they call it risk ), higher risk investments are expected to realize higher returns, on average”.
- 4. Principles Applied Principle 4: Market Prices Reflect Information “ help us understand the wisdom of markets and how investors purchases and sales of a security drive its price to reflect everything that is known about the security’s risk and expected return”.
- 5. INTRO : “TRUST FUND BABY ” January, 1926, $100 – December, 2009 Long term bond issued by the US gov’t 5.4% $8,400 Portfolio of large US stocks 9.8% $259,200 Portfolio of the smallest publicly traded firms 11.9% $1.2M
- 6. INTRO : “TRUST FUND BABY ” First, how do we measure the risk and return for an individual investment? Second, what is the history of financial market returns on various classes of financial assets, including domestic and international debt and equity securities as well as real estate and commodities? Finally, what returns should investors expect from investing in risky financial assets?
- 7. Calculating the RealizedReturn from an Investment Realized return or cash return measures the gain or loss on an investment.
- 8. Calculating the RealizedReturn from an Investment Example 1 : You invested in 1 share of Apple (AAPL) for $95 and sold a year later for $200. The company did not pay any dividend during that period. What will be the cash return on this investment?
- 9. Calculating the RealizedReturn from an Investment Cash Return = $200 + 0 - $95 = $105
- 10. Calculating the RealizedReturn from an Investment We can also calculate the rate of return as a percentage. It is simply the cash return divided by the beginning stock price.
- 11. Calculating the RealizedReturn from an Investment Example 2: You invested in 1 share of share Apple (AAPL) for $95 and sold a year later for $200. The company did not pay any dividend during that period. What will be the rate of return on this investment?
- 12. Calculating the RealizedReturn from an Investment Rate of Return = ($200 + 0 - $95) ÷ $95 = 110.53% Table 7-1 has additional examples on measuring an investor’s realized rate of return from investing in common stock.
- 14. Calculating the RealizedReturn from an Investment Table 7-1 indicates that the returns from investing in common stocks can be positive or negative. Furthermore, past performance is not an indicator of future performance. However, in general, we expect to receive higher returns for assuming more risk.
- 15. Calculating the ExpectedReturn from an Investment Expected return - average of the possible returns, where each possible return is weighted by the probability that it occurs.
- 17. Calculating the ExpectedReturn from an Investment Expected Return = (-10% × 0.2) + (12% × 0.3) + (22% × 0.5) = 12.6%
- 18. Measuring Risk In theexample on Table 7-2, the expected return is 12.6%; however, the return could range from -10% to +22%. This variability in returns can be quantified by computing the Variance or Standard Deviation in investment returns.
- 19. Measuring Risk Variance –average squared difference between the individual realized returns and the expected return. Standard deviation – square root of the variance.
- 20. Calculating the Varianceand Standard Deviation of the Rate of Return on an Investment Let us compare two possible investment alternatives: (1) U.S. Treasury Bill –short-term debt obligation of the U.S. Government. Assume this particular Treasury bill matures in one year and promises to pay an annual return of 5%. U.S. Treasury bill is considered risk-free as there is no risk of default on the promised payments. (2) Common stock of the Ace Publishing Company – an investment in common stock will be a risky investment.
- 21. Calculating the Varianceand Standard Deviation of the Rate of Return on an Investment The probability distribution of an investment’s return contains all possible rates of return from the investment along with the associated probabilities for each outcome. Figure 7-1 contains a probability distribution for U.S. Treasury bill and Ace Publishing Company common stock.
- 23. Calculating the Varianceand Standard Deviation of the Rate of Return on an Investment The probability distribution for Treasury bill is a single spike at 5% rate of return indicating that there is 100% probability that you will earn 5% rate of return. The probability distribution for Ace Publishing company stock includes returns ranging from -10% to 40% suggesting the stock is a risky investment.
- 24. Calculating the Varianceand Standard Deviation of the Rate of Return on an Investment Using equation 7-3, we can calculate the expected return on the stock to be 15% while the expected return on Treasury bill is always 5%. Does the higher return of stock make it a better investment? Not necessarily, we also need to know the risk in both the investments.
- 25. Calculating the Varianceand Standard Deviation of the Rate of Return on an Investment We can measure the risk of an investment by computing the variance as follows:
- 27. Calculating the Varianceand Standard Deviation of the Rate of Return on an Investment Investment Treasury Bill Common Stock Expected Return 5% Standard Deviation 0% 15% 12.85% So we observe that the publishing company stock offers a higher expected return but also entails more risk as measured by standard deviation. An investor’s choice of a specific investment will be determined by their attitude toward risk.
- 28. A Brief Historyof Financial Market Returns We can use the tools that we have learned to determine the risk-return tradeoff in the financial markets.
- 29. A Brief Historyof the Financial Markets Investors have historically earned higher rates of return on riskier investments. However, having a higher expected rate of return simply means that investors “expect” to realize a higher return. Higher return is not guaranteed.
- 30. U.S. Financial Markets:Domestic Investment Returns Small stocks: shares of the smallest 20% of all companies whose stock is traded on the public exchanges. ( Firm size is measured using the market capitalization of the company’s equity, which is equal to the share price multiplied by the number of shares outstanding. ) Large stocks: the Standard & Poor’s (S&P) 500 stock index, which is a portfolio that consists large company stocks such as Walmart (WMT), Intel (INTC), and Microsoft (MSFT). Gov’t bonds: 20-year bonds issued by the federal gov’t. These bonds are typically considered to be free of the risk of default or non-payment since the gov’t is the most credit-worthy borrower in the country. Treasury bills: short-term securities issued by the federal gov’t that have maturities of one year or less.
- 31. U.S. Financial Markets:Domestic Investment Returns Small Stocks Large Stocks Gov’t Bonds Treasury Bill Compound annual return 11.9% 9.8% 5.4% 3.7% Standard deviation 20.5% 9.6% 3.1% 32.8% LESSONS LEARNED: Lesson #1: The riskier investments have historically realized higher returns. Lesson #2: The historical returns of the higherrisk investment classes have standard deviations.
- 32.
- 33. Geometric vs. Arithmetic AverageRates of Return Arithmetic average may not always capture the true rate of return realized on an investment. In some cases, geometric or compound average may be a more appropriate measure of return.
- 34. Geometric vs. Arithmetic AverageRates of Return For example, suppose you bought a stock for $25. After one year, the stock rises to $30 and in the second year, it falls to $15. What was the average return on this investment?
- 35. Geometric vs. Arithmetic AverageRates of Return The stock earned +20% in the first year and -50% in the second year. Simple average = (20%-50%) ÷ 2 = -15%
- 36. Geometric vs. Arithmetic AverageRates of Return However, over the 2 years, the $25 stock lost the equivalent of 22.54% ({($15/$25)1/2} - 1 = 22.54%). Here, -15% is the simple arithmetic average while -22.54% is the geometric or compound average rate. Which one is the correct indicator of return? It depends on the question being asked.
- 37. Geometric vs. Arithmetic AverageRates of Return The geometric average rate of return answers the question, “What was the growth rate of your investment?” The arithmetic average rate of return answers the question, “What was the average of the yearly rates of return?
- 38. Computing the Geometricor Compound Average Rate of Return
- 39. Computing the Geometricor Compound Average Rate of Return Compute the arithmetic and geometric average for the following stock. Year Annual Rate of Return Value of the stock $25 1 40% $35 2 -50% $17.50 0
- 40. Computing the Geometricor Compound Average Rate of Return Arithmetic Average = (40-50) ÷ 2 = -5% Geometric Average = [(1+Ryear1) × (1+Ryear 2)]1/2 - 1 = [(1.4) × (.5)] 1/2 - 1 = -16.33%
- 41. Choosing the Right“Average” Both arithmetic average geometric average are important and correct. The following grid provides some guidance as to which average is appropriate and when: Question being addressed: What annual rate of return can we expect for next year? What annual rate of return can we expect over a multi-year horizon? Appropriate Average Calculation: The arithmetic average calculated using annual rates of return. The geometric average calculated over a similar past period.
- 42. What Determines StockPrices? In short, stock prices tend to go up when there is good news about future profits, and they go down when there is bad news about future profits. Since US businesses have generally done well over the past 80 years, the stock returns have also been favorable.
- 43. The Efficient MarketHypothesis The efficient market hypothesis (EMH) states that securities prices accurately reflect future expected cash flows and are based on information available to investors. An efficient market is a market in which all the available information is fully incorporated into the prices of the securities and the returns the investors earn on their investments cannot be predicted.
- 44. The Efficient MarketHypothesis We can distinguish among three types of efficient market, depending on the degree of efficiency: 1. 2. 3. The Weak-Form Efficient Market Hypothesis The Semi-Strong Form Efficient Market Hypothesis The Strong Form Efficient Market Hypothesis
- 45. The Efficient MarketHypothesis (1) The Weak-Form Efficient Market Hypothesis asserts that all past security market information is fully reflected in security prices. This means that all price and volume information is already reflected in a security’s price.
- 46. The Efficient MarketHypothesis (2) The Semi-Strong-Form Efficient Market Hypothesis asserts that all publicly available information is fully reflected in security prices. This is a stronger statement as it includes all public information (such as firm’s financial statements, analysts’ estimates, announcements about the economy, industry, or company.)
- 47. The Efficient MarketHypothesis (3) The Strong-Form Efficient Market Hypothesis asserts that all information, regardless of whether this information is public or private, is fully reflected in securities prices. It asserts that there isn’t any information that isn’t already embedded into the prices of all securities.