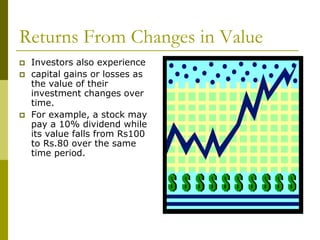
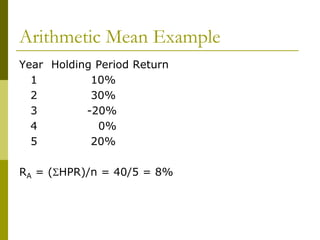
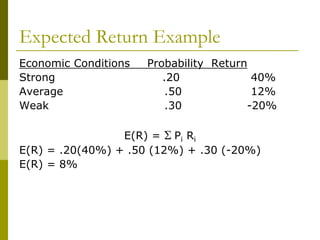
This document discusses sources of investment returns and how to measure risk and returns. It provides the following key points: - Investments provide two basic types of returns: income returns from cash flows and returns from changes in the investment's price or value over time. - Total return on an investment considers both income received and capital gains/losses. Various measures can quantify returns, including arithmetic mean, geometric mean, and expected rates of return. - Risk refers to the uncertainty of investment returns and is measured by the variability of possible outcomes. The total risk of an investment includes systematic and unsystematic components. Systematic risk cannot be eliminated by diversification, while unsystematic risk can be reduced through diversification

1. Risk & Return
Dr Aloysius Edward J
Dean, Faculty of Commerce and
Management
Kristu Jayanti College Autonomous
Bangalore

2. Sources of Investment Returns
 Risk and Return go together in investments.
 Everything an investor ( be it the company or the
investors in the company) does is tied directly or
indirectly to return and risk.
 Return is the motivating force, inspiring the
investor in the form of rewards, for undertaking
the investment.
Investments provide two basic types of return:
 Income returns
 The owner of an investment has the right to any cash
flows paid by the investment.
 Changes in price or value
 The owner of an investment receives the benefit of
increases in value and bears the risk for any decreases

3. Income Returns
 Cash payments,
usually received
regularly over the life
of the investment.
 Examples: Coupon
interest payments
from bonds, Common
and preferred stock
dividend payments.

4. Returns From Changes in Value
 Investors also experience
 capital gains or losses as
the value of their
investment changes over
time.
 For example, a stock may
pay a 10% dividend while
its value falls from Rs100
to Rs.80 over the same
time period.

5. Investment Strategy
 Generally, the income returns from an
investment are “in your pocket” cash flows.
 Over time, your portfolio will grow much faster if
you reinvest these cash flows and put the full
power of compound interest in your favor.
 Dividend reinvestment plans (DRIPs) provide a
tool for this to happen automatically; similarly,
Mutual Funds allow for automatic reinvestment of
income.

6. Measuring Returns
 Total Returns
 How much money was made on an investment over
some period of time?
 Total Return = Income + Price Change
 Current return
The periodic cash receipts or income on investment
in the form of interest, dividends etc.
Capital Return
It is simply the price appreciation ( or depreciation)
divided by the beginning price of the asset. For
assets like equity stocks, the capital return
predominates.

7. To continue
Total return = Current return + Capital
Return.
The current return can be zero or positive,
whereas the capital return can be
negative, zero or positive.
Equation = D/I + ( CP/sp – BP/pp) / BP/pp.

8. Annualized Returns
 If we have return or income/price change
information over a time period in excess of one
year, we usually want to annualize the rate of
return in order to facilitate comparisons with
other investment returns.
 Another useful measure:
Return Relative = Income + Ending Value
Purchase Price

9. Two Types of Return
 There are two types of return :
1. Realized or Historical Return
2. Expected Return
1.Realized Return
This is ex-post return, or return that was or
could have been earned.
For Eg. A deposit of Rs.1000 in a bank on
Jan.1 at a stated annual interest of 10%
will be worth Rs.1100 exactly a year later.
The historical return in this case is 10%.

10. Measuring Historic Returns
 Starting with annualized Holding Period
Returns, we often want to calculate some
measure of the “average” return over time
on an investment.
 Two commonly used measures of
average:
 Arithmetic Mean
 Geometric Mean

11. Arithmetic Mean Return
 The arithmetic mean is the “simple average” of a
series of returns.
 Calculated by summing all of the returns in the
series and dividing by the number of values.
RA = (SHPR)/n
 Oddly enough, earning the arithmetic mean
return for n years is not generally equivalent to
the actual amount of money earned by the
investment over all n time periods.

12. Arithmetic Mean Example
Year Holding Period Return
1 10%
2 30%
3 -20%
4 0%
5 20%
RA = (SHPR)/n = 40/5 = 8%

13. Geometric Mean Return
 The geometric mean reflects the
compound rate of growth over time.
 It is calculated as the nth root of the
product of all of the n return relatives of
the investment.
RG = [P(Return Relatives)]1/n – 1
Return relative = 1 + Total Return

14. Geometric Mean Example
Year Holding Period Return Return Relative
1 10% 1.10
2 30% 1.30
3 -20% 0.80
4 0% 1.00
5 20% 1.20
RG = [P(Return Relatives)]1/n – 1
RG = [(1.10)(1.30)(.80)(1.00)(1.20)]1/5 – 1
RG = .0654 or 6.54%

15. Arithmetic Mean vs Geometric
Mean
 The Arithmetic mean is a more appropriate
measure of average performance over single
period
 The Geometric mean is a better measure of
growth in wealth over time
 The Geometric mean is always less than the
arithmetic mean, except when all the return
values being considered equal.

16. Scenario Analysis
 While historic returns, or past realized returns,
are important, investment decisions are
inherently forward-looking.
 We often employ scenario or “what if?” analysis
in order to make better decisions, given the
uncertain future.
 Scenario analysis involves looking at different
outcomes for returns along with their associated
probabilities of occurrence.

17. Expected Rates of Return
 Expected rates of return are calculated by
determining the possible returns (Ri) for
some investment in the future, and
weighting each possible return by its own
probability (Pi).
E(R) = S Pi Ri

18. Expected Return Example
Economic Conditions Probability Return
Strong .20 40%
Average .50 12%
Weak .30 -20%
E(R) = S Pi Ri
E(R) = .20(40%) + .50 (12%) + .30 (-20%)
E(R) = 8%

19. What is risk?
 Risk is the uncertainty associated with the return
on an investment.
 One can not talk about returns without talking
about risk.
 All the investment decisions involve a trade-off
between the two.
 Risk refers to the possibility that actual outcome
of an investment will differ from its expected
income.
 This means that the more variable the possible
outcomes that can occur, the greater risk.
 Put differently, risk refers to variability. If an
asset’s return has no variability, it is risk less.

20. Sources of Risk OR Elements of Risk
 The total variability in returns of a security
represents the total risk of that security.
 Total risk = systematic risk +
unsystematic risk
 Systematic risk : The impact of economic,
political and social changes is system-wide
and that portion of total variability in
security returns caused by such system-
wide factors is known as Systematic risk.

21. To continue
NON-DIVERSIFIABLE RISK FACTORS :
Major changes in tax rates
War & other calamities
An increase or decrease in inflation rates
A change in economic policy
Industrial recession
An increase in the international oil prices
COVID 19 Pandemic

22. To continue
 These are factors which are external to a
company ( that is related to the general economy
or the stock market as a whole ) and affect a
large number of securities simultaneously. It can
not be eliminated . These are mostly
uncontrollable in nature. It is known as
SYSTEMATIC RISK or NON-DIVERSIFIABLE RISK.
 It is sub divided into
 Interest rate risk
 Market risk
 Purchasing power risk

23. Unsystematic Risk
 The returns from a security may sometimes vary
because of certain factors affecting only the
company issuing such security.
 When variability of returns occurs because of
such firms – specific factors it is known as
unsystematic risk.
Those factors which are internal to companies and
affect only those particular companies. It is
known as DIVERSIFIABLE RISK OR
UNSYSTEMATIC RISK OR SPECIFIC RISK.

24. To continue
 Factors : - Raw material scarcity
- Labour strike
- Management inefficiency
- Death of a key company Officer
- Unexpected entry of new
competitor into the market
Two Types of Unsystematic risk
- Business Risk
-Financial Risk

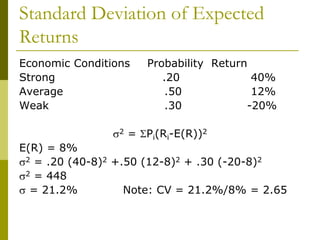
25. How can we measure risk?
 Since risk is related to variability and uncertainty,
we can use measures of variability to assess risk.
 The variance and its positive square root, the
standard deviation, are such measures.
 Measure “total risk” of an investment, the combined
effects of systematic and unsystematic risk.
 Variance of Historic Returns
s2 = [S(Rt-RA)2]/n-1

26. Standard Deviation of Historic
Returns
Year Holding Period Return
1 10% RA = 8%
2 30% s2 = 370
3 -20% s = 19.2%
4 0%
5 20%
s2 = [S(Rt-RA)2]/n-1
s2 = [(10-8)2+(30-8)2+(-20-8)2+(0-8)2+(20-8)2]/4
= [4+484+784+64+144]/4
= [1480]/4

27. Coefficient of Variation
 The coefficient of variation is the ratio of the
standard deviation divided by the return on the
investment; it is a measure of risk per unit of
return.
CV = s/RA
 The higher the coefficient of variation, the riskier
the investment.
 From the previous example, the coefficient of
variation would be:
CV =19.2%/8% = 2.40

28. Measuring Risk : Expected Return
 If we are considering various scenarios of
return in the future, we can still calculate
the variance and standard deviation of
returns, now just from a probability
distribution.
s2 = SPi(Ri-E(R))2

29. Standard Deviation of Expected
Returns
Economic Conditions Probability Return
Strong .20 40%
Average .50 12%
Weak .30 -20%
s2 = SPi(Ri-E(R))2
E(R) = 8%
s2 = .20 (40-8)2 +.50 (12-8)2 + .30 (-20-8)2
s2 = 448
s = 21.2% Note: CV = 21.2%/8% = 2.65