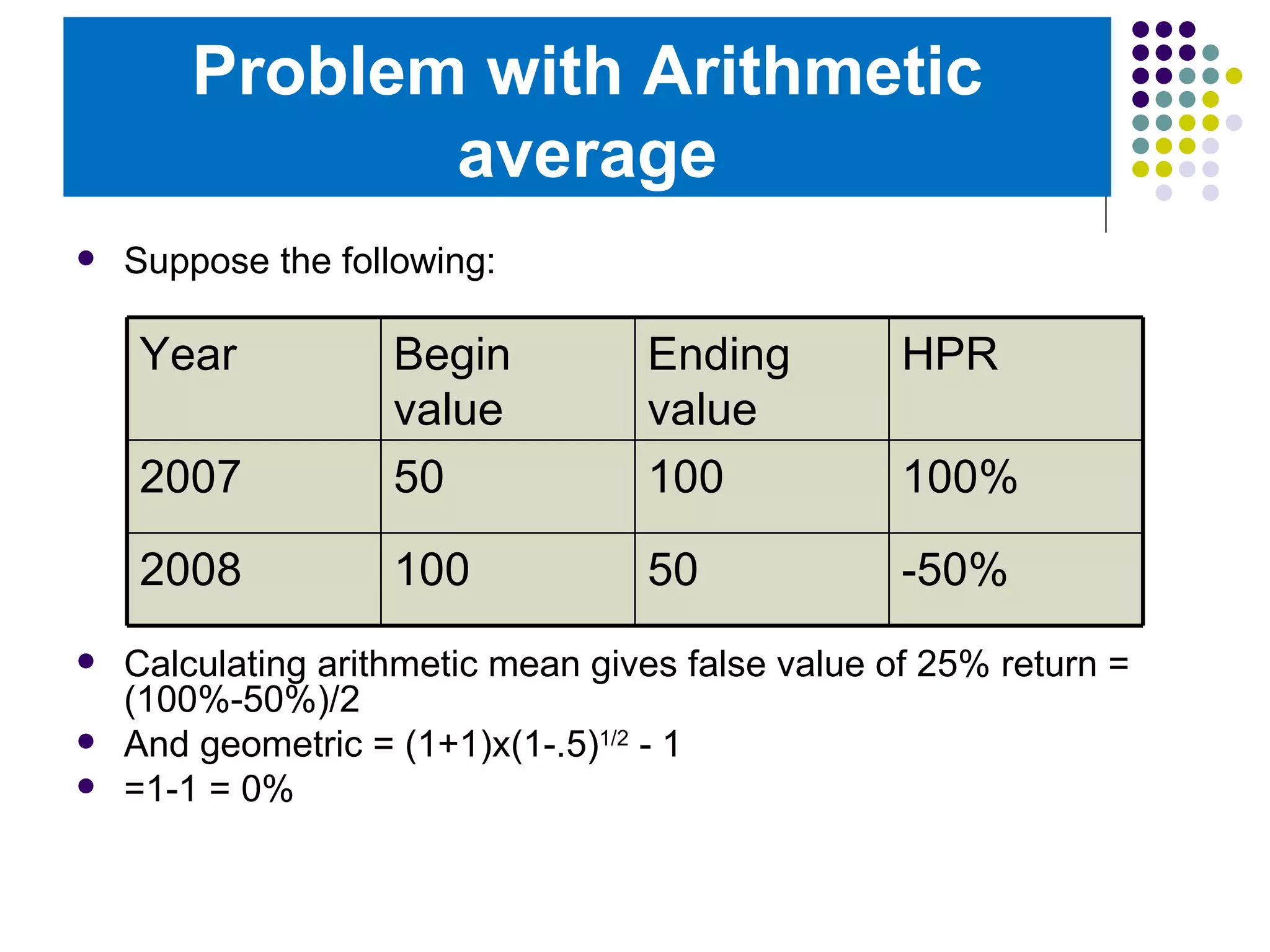
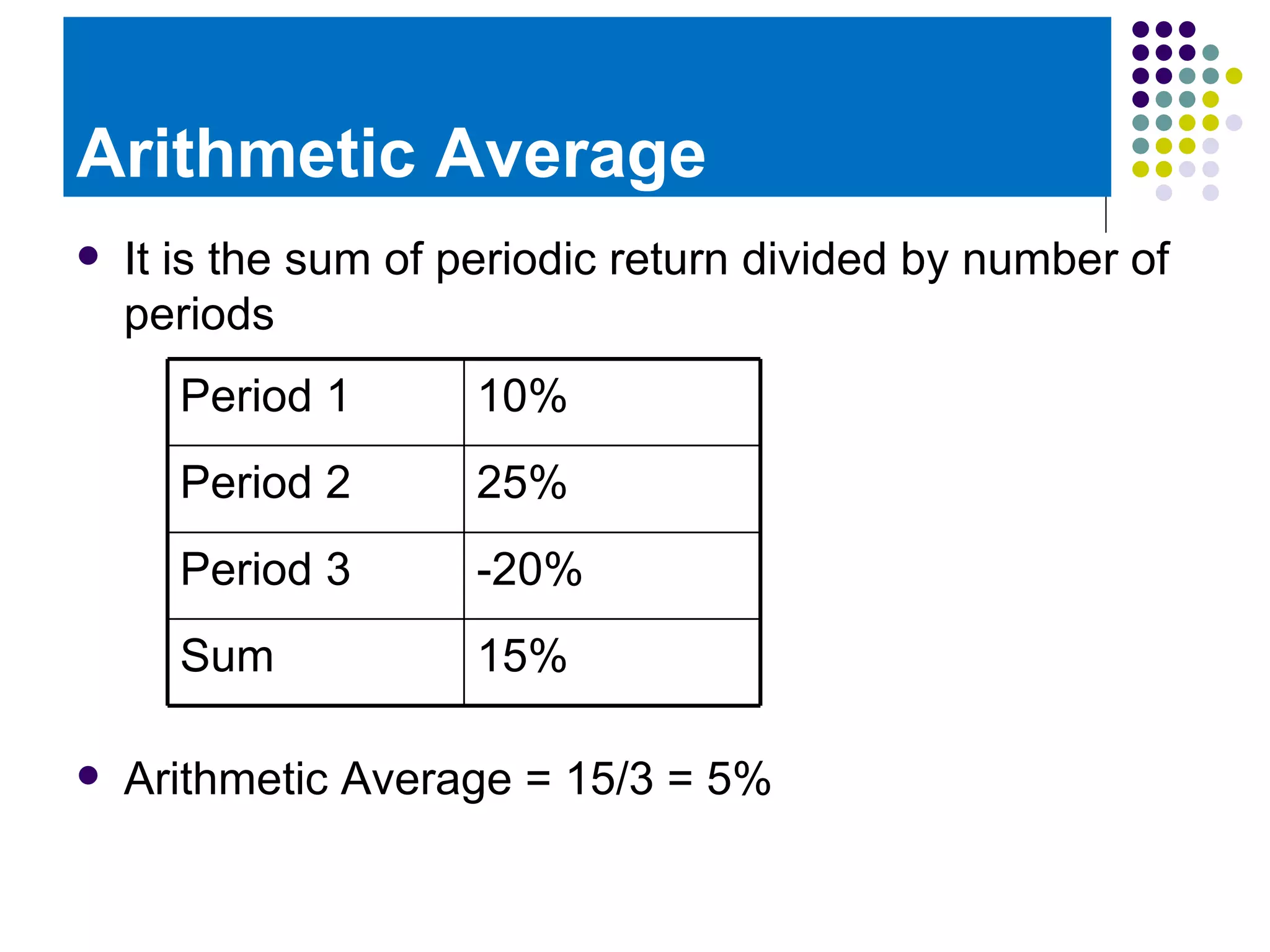
The document discusses different methods for calculating rates of return on investments over time. It defines holding period return as the capital gain plus any cash dividends, divided by the initial price. It also defines dividend yield. There are three main methods discussed: arithmetic average, which simply averages the periodic returns; geometric average, which finds the nth root of the product of 1 plus the rate of return for each period; and dollar weighted return. The geometric average is preferred when returns vary widely from period to period, as the arithmetic average can overstate performance in that case.

1. Lecture 10 Return and Risk

2. Rates of Return A key measure of investors’ success is the rate at which their funds have grown Holding-period return (HPR) of shares is composed of capital gain and dividend HPR = (P1-Po + Cash Dividend)/Po This definition assumes end of period returns and ignores re-investment of income

3. Rates of Return Dividend Yield = Percentage return from dividends i.e. (Dividend x100)/Po To calculate HPR over a period of time, we can use: Arithmetic average Geometric average Dollar weighted return

4. Arithmetic Average It is the sum of periodic return divided by number of periods Arithmetic Average = 15/3 = 5% Period 1 10% Period 2 25% Period 3 -20% Sum 15%

5. Geometric Average nth root of the product of returns for n years Geometric mean = (1+R 1 )x(1+R 2 )x(1+R 3 ) 1/n – 1 = [(1+10%) x (1+ 25%) x(1+(-20%))] 1/3 – 1 [(1.1) x (1.25) x (.8)] 1/3 – 1 (1.1) 1/3 – 1 1.03-1 .03 or 3%

6. Problem with Arithmetic average Suppose the following: Calculating arithmetic mean gives false value of 25% return = (100%-50%)/2 And geometric = (1+1)x(1-.5) 1/2 - 1 =1-1 = 0% Year Begin value Ending value HPR 2007 50 100 100% 2008 100 50 -50%

7. Geometric Vs Arithmetic In highly volatile security prices, arithmetic mean is biased upward and we should use geometric mean If rates of returns are the same for all years, geometric and arithmetic averages gives same results