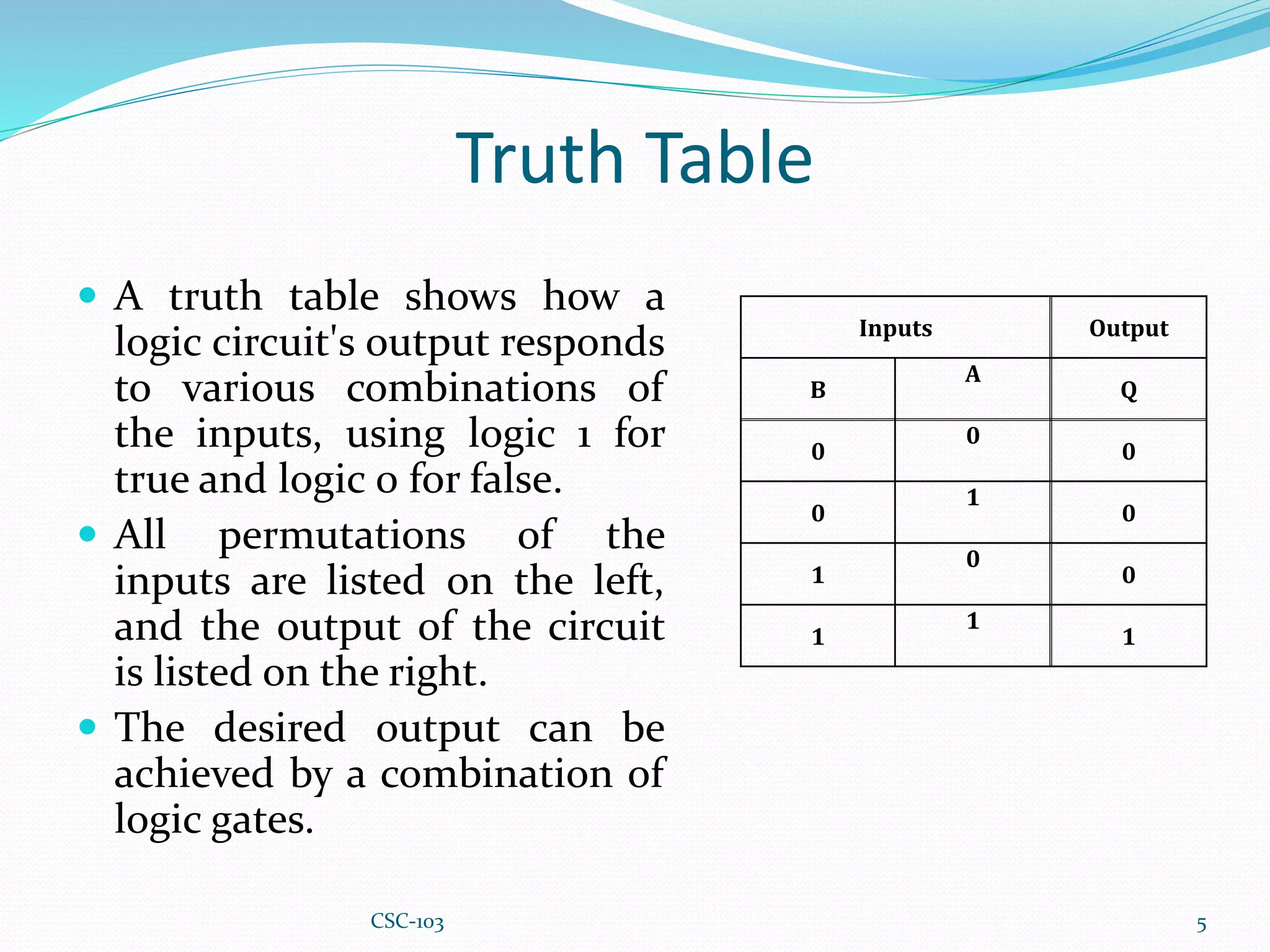
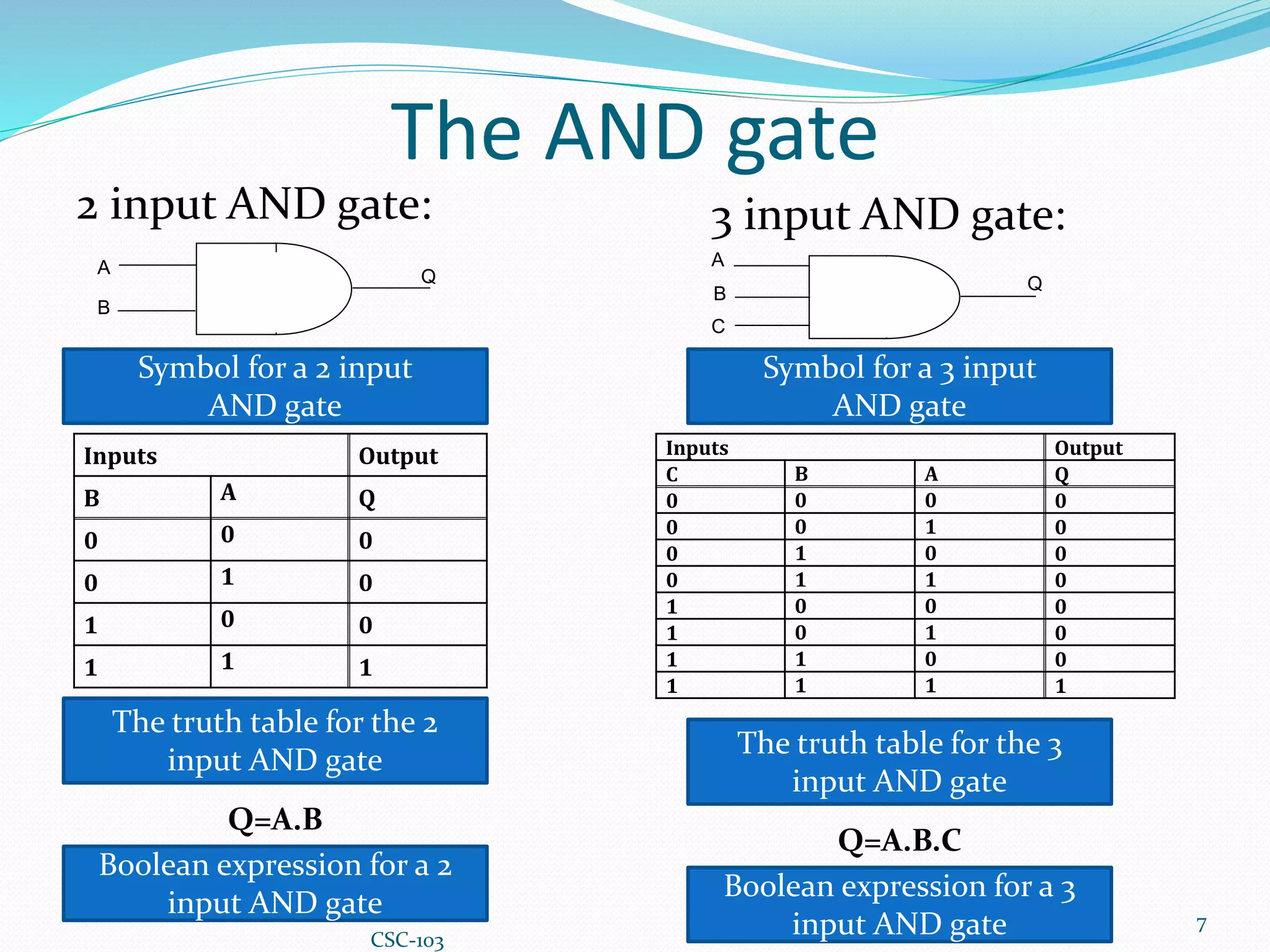
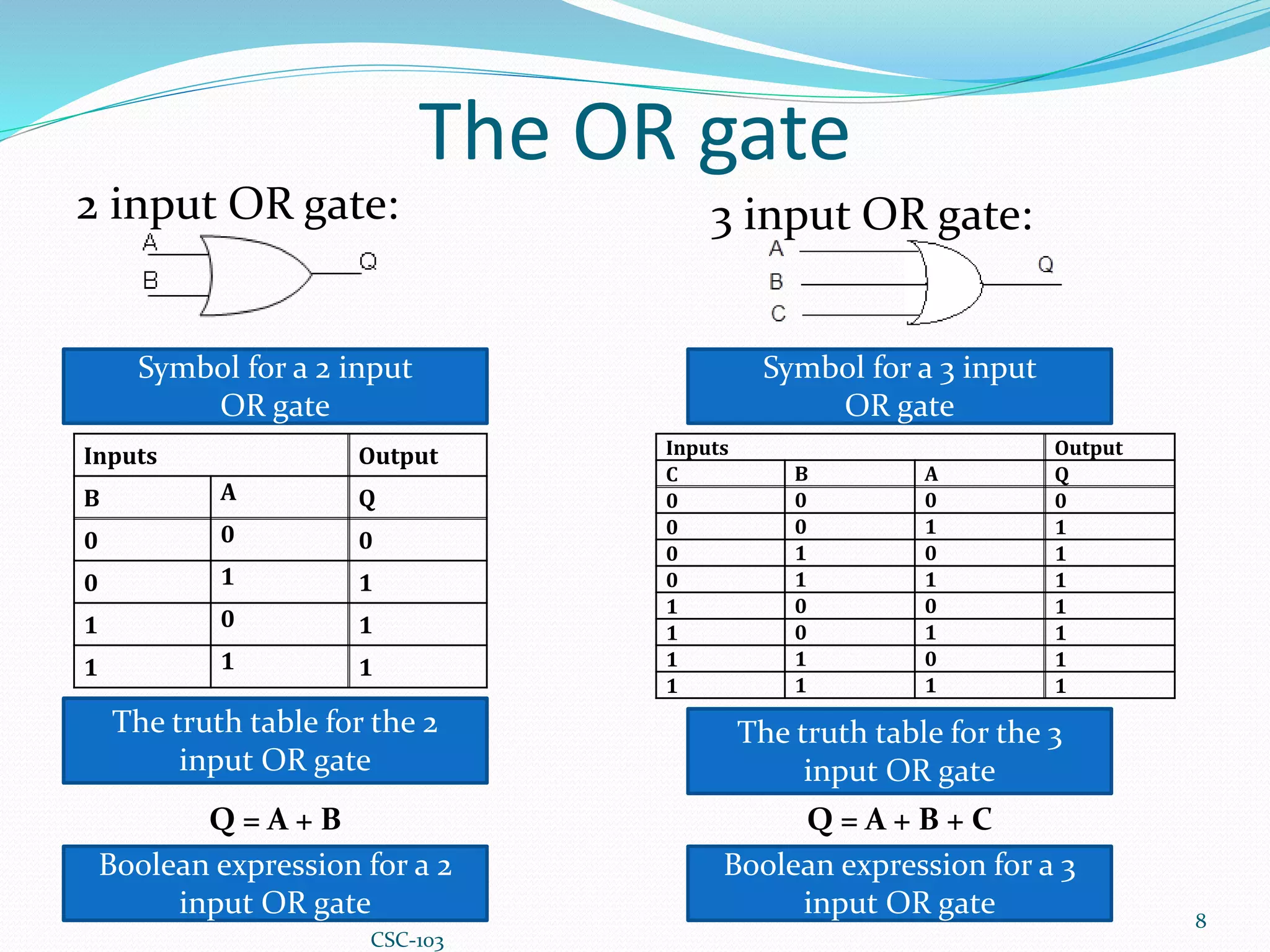
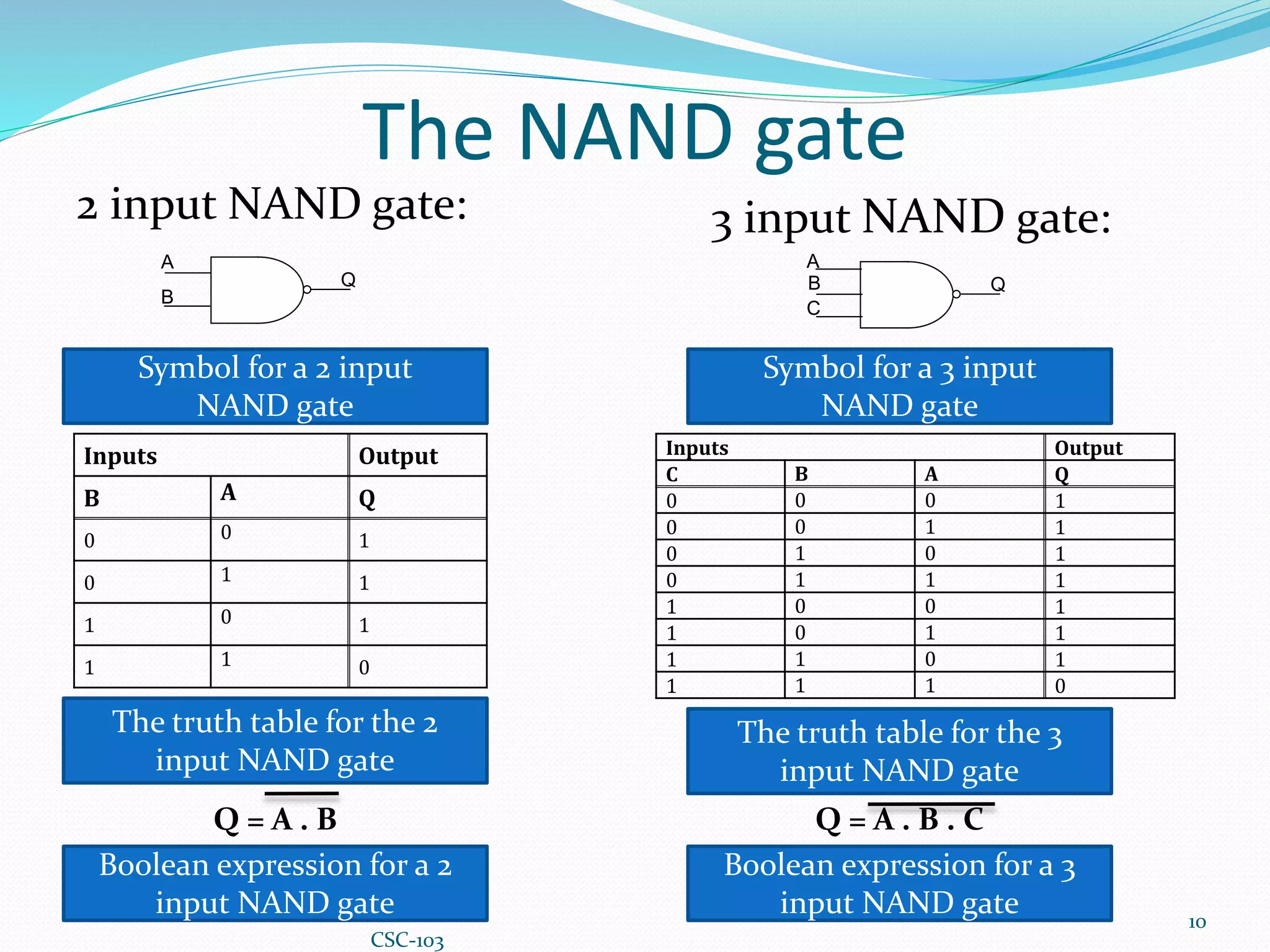
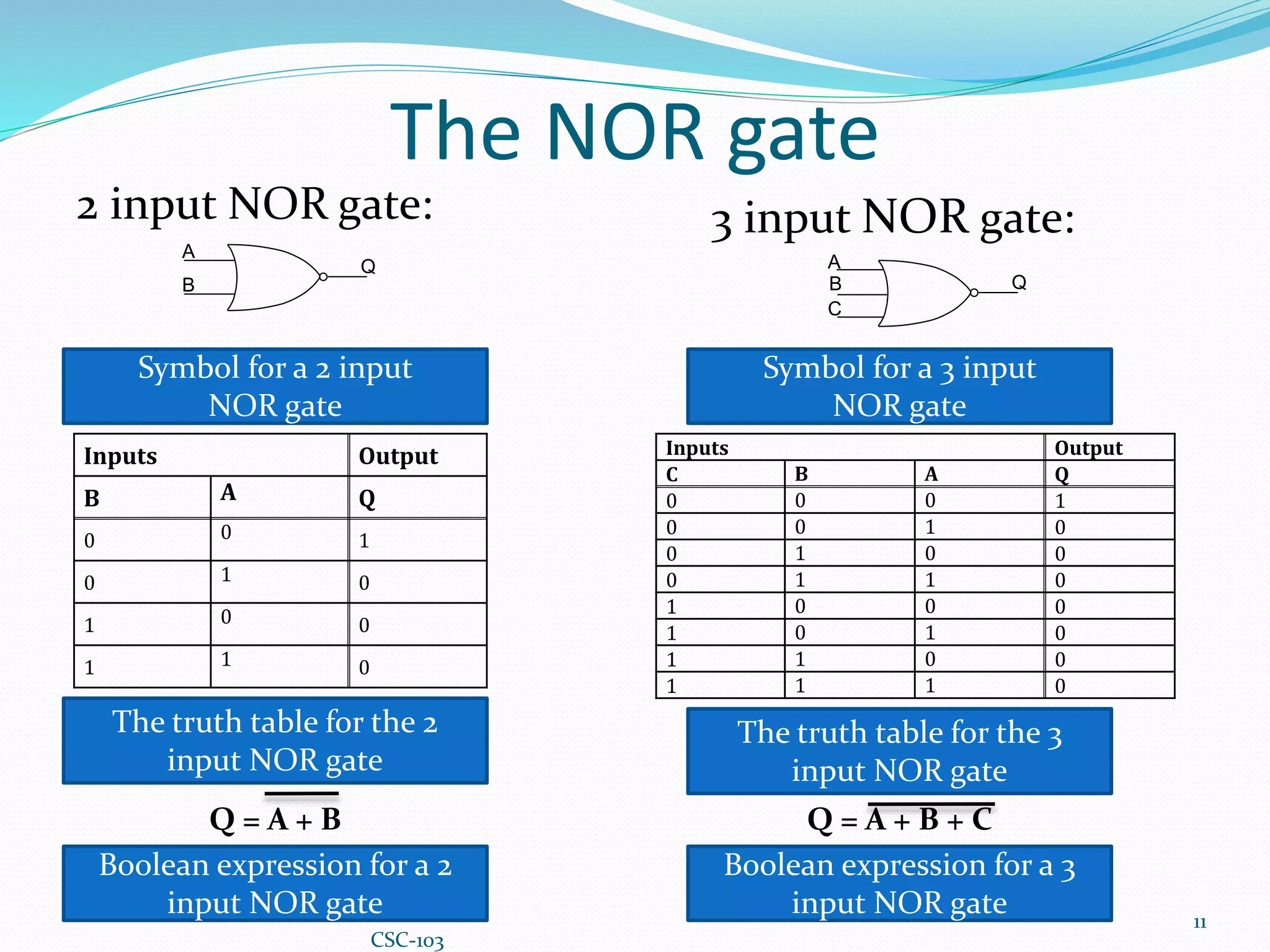
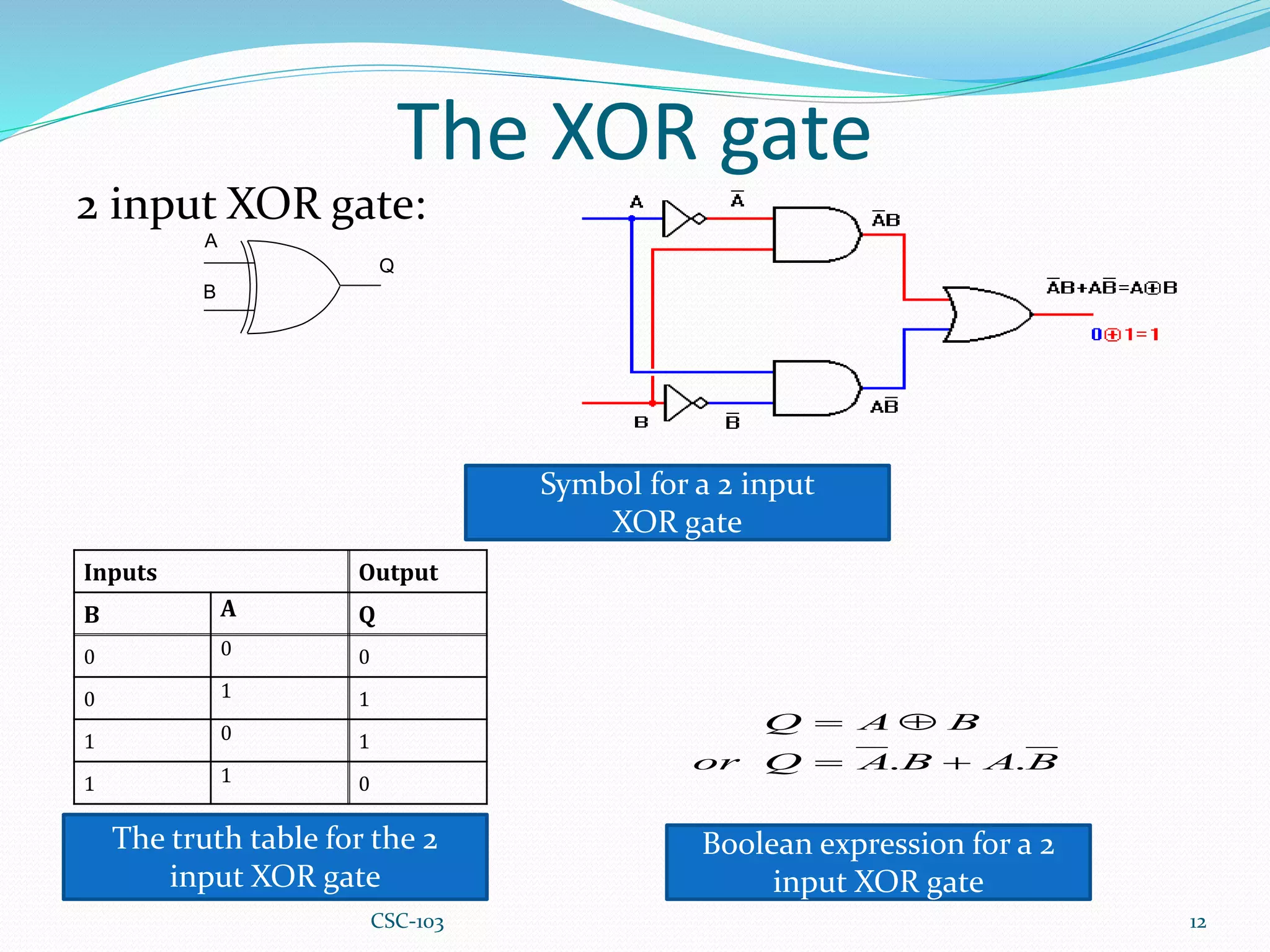
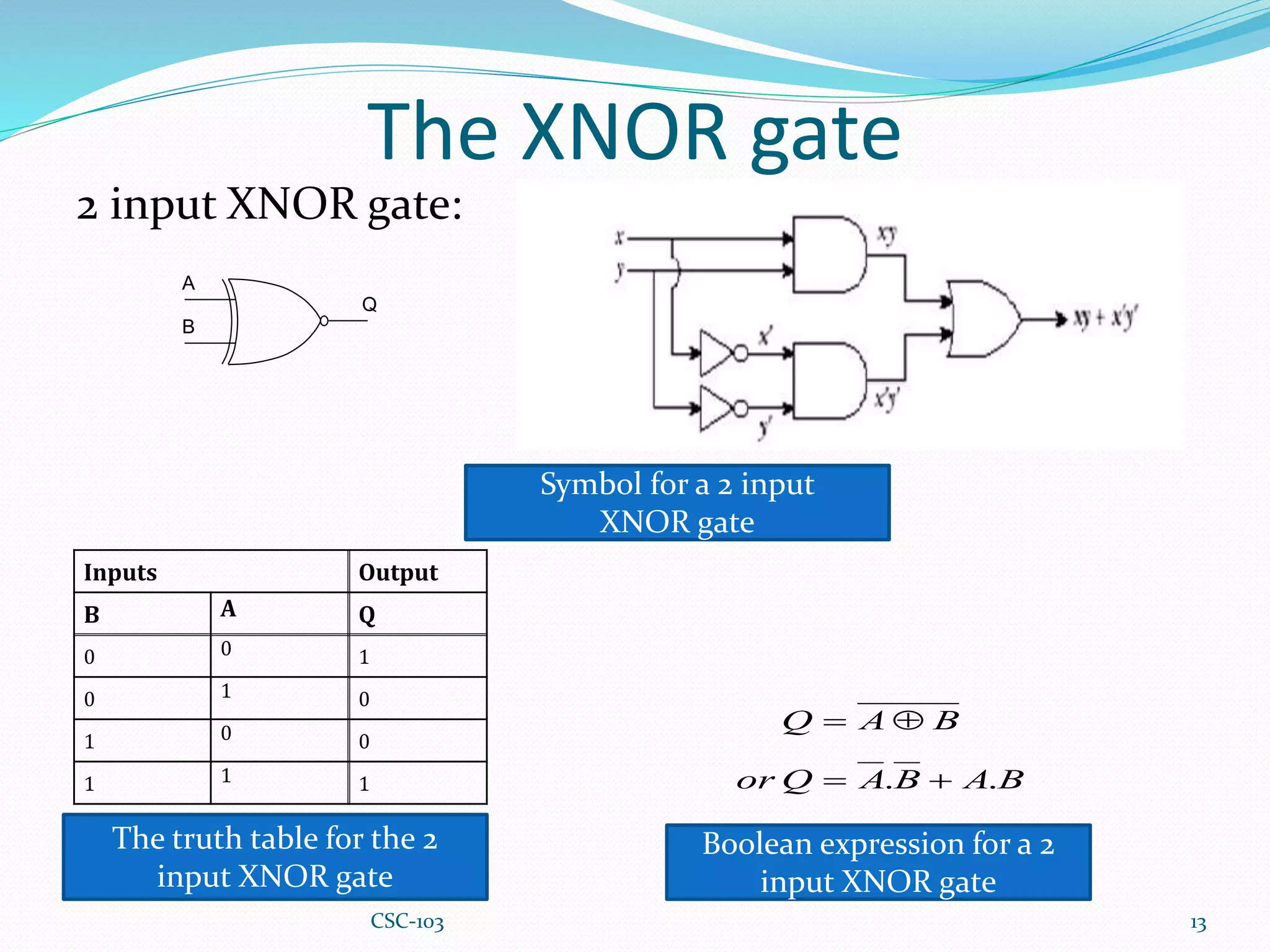
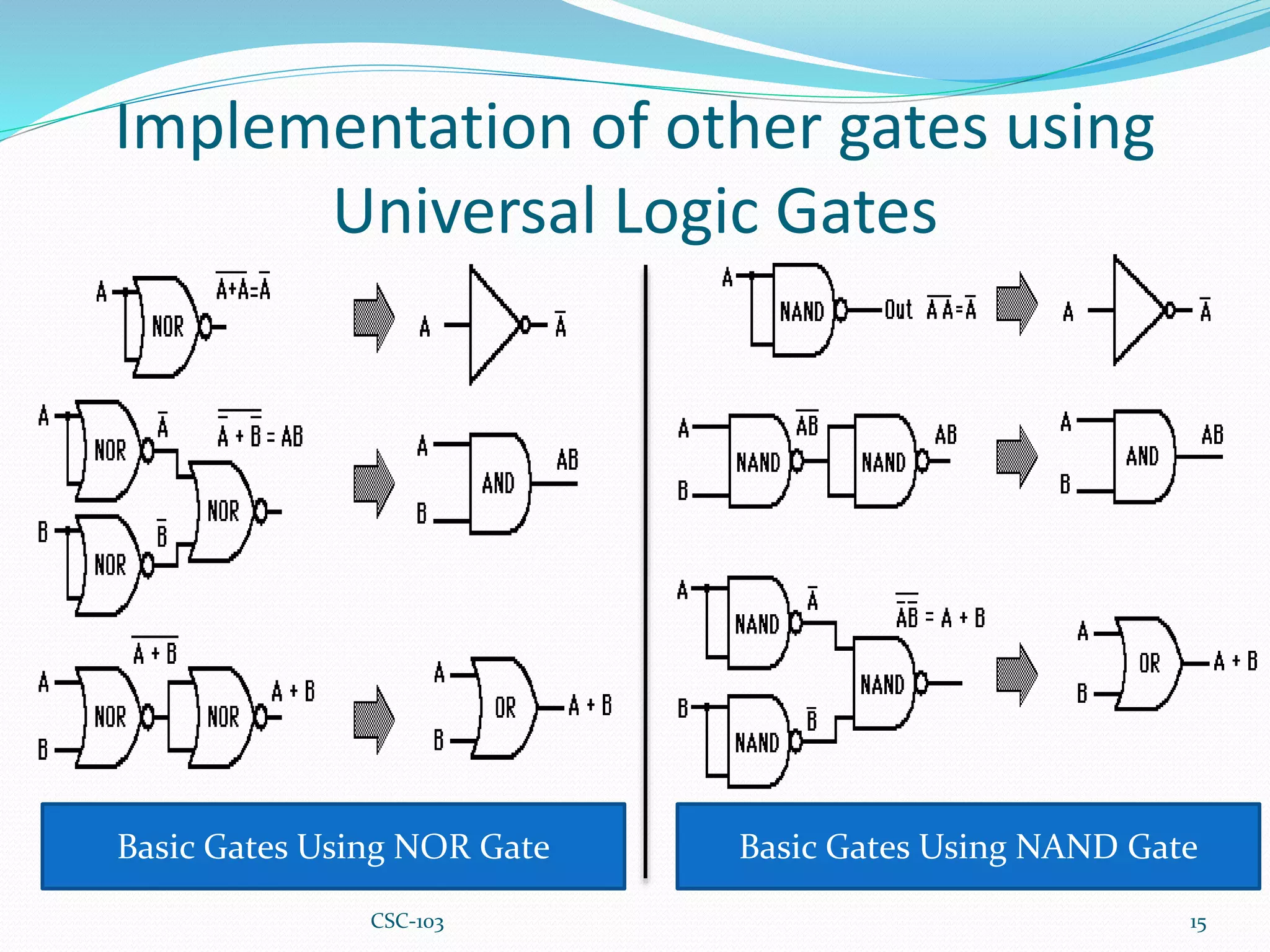
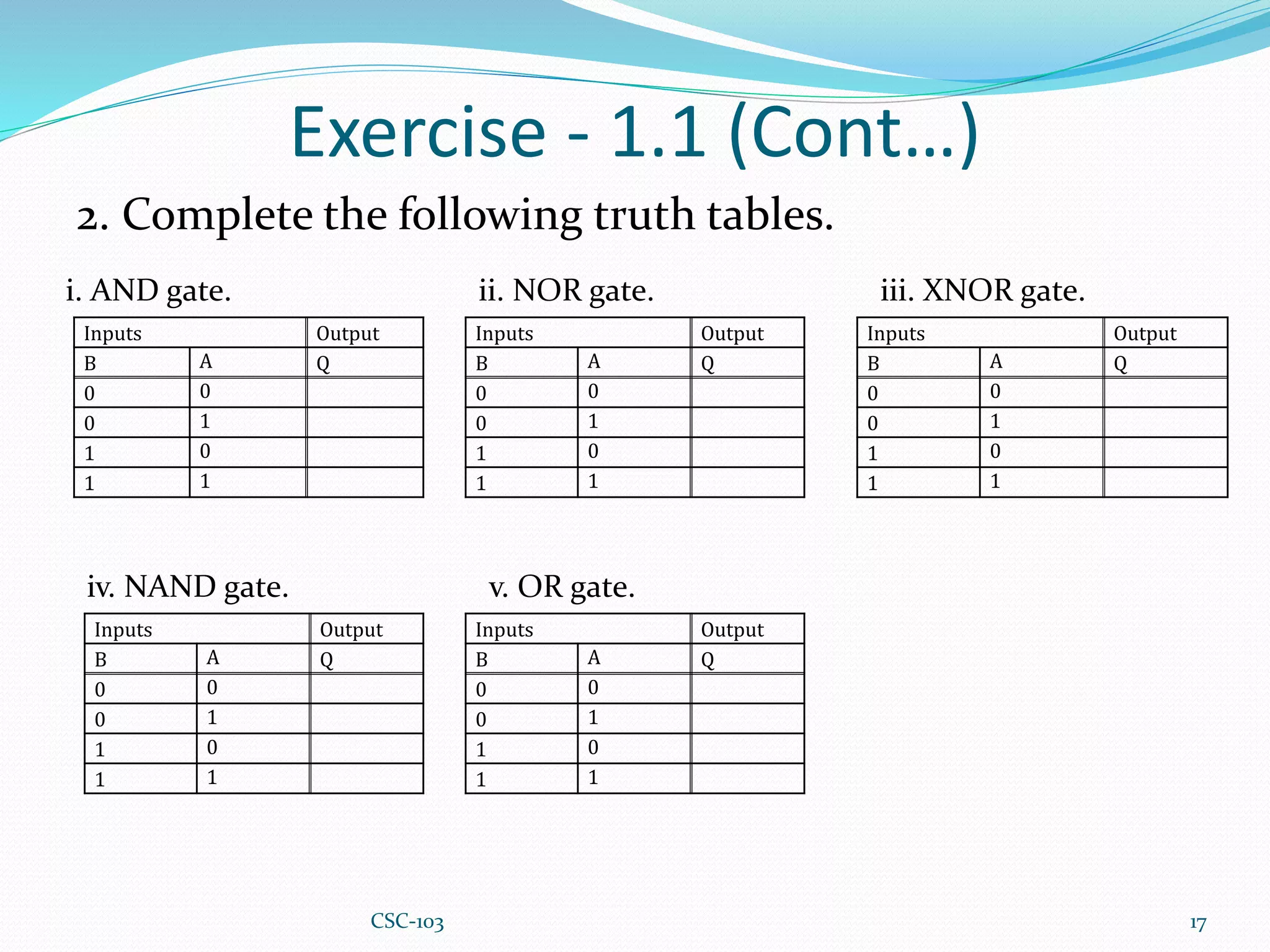
This document provides information about Boolean algebra and logic gates. It defines Boolean algebra and explains that it is important in computer science for representing binary signals. It then defines logic gates as the basic building blocks of digital circuits, and describes common logic gates like AND, OR, NOT, NAND, NOR, XOR, and XNOR. Truth tables are presented as a way to represent the output of logic gates for all possible input combinations. The document also notes that NAND and NOR gates are considered "universal gates" since other gates can be represented using only these gate types. It provides examples of implementing other gates using only NAND or NOR gates. Finally, it discusses how to convert between Boolean expressions and logic gate circuits.

1. CSC-103 1

2. Outcome of this chapter
 Knowledge about logic gates, their expression, input
and output.
 Know how to draw circuits for Boolean expression.
 Know how to express a circuit through Boolean
expression.
2
CSC-103

3. Boolean Algebra
 Boolean algebra is the mathematics of Boolean logic,
where statements are evaluated to be either true or
false.
 It is extremely important in computer sciences, such
as programming, database querying and computer
engineering, as electrical signals at the most basic
level are translated to and from binary (true/false,
1/0, on/off, closed/open, etc).
3
CSC-103

4. Logic Gate
 A logic gate is an elementary building block of a digital
circuit.
 A Logic Gate in an electronic sense makes a ‘logical’
decision based upon a set of rules, and if the
appropriate conditions are met then the gate is
opened, and an output signal is produced.
 Most logic gates have two inputs and one output.
 At any given moment, every terminal is in one of the
two binary conditions low (0) or high (1), represented
by different voltage levels.
4
CSC-103

5. Truth Table
 A truth table shows how a
logic circuit's output responds
to various combinations of
the inputs, using logic 1 for
true and logic 0 for false.
 All permutations of the
inputs are listed on the left,
and the output of the circuit
is listed on the right.
 The desired output can be
achieved by a combination of
logic gates.
Inputs Output
B
A
Q
0
0
0
0
1
0
1
0
0
1
1
1
5
CSC-103

6. Logic Gates
Fundamental Logic Gates:
 AND gate
 OR gate
 NOT gate
Universal Logic Gates:
 NAND gate
 NOR gate
Special Logic Gates:
 XNOR gate
 XOR gate
6
CSC-103

7. The AND gate
2 input AND gate:
7
A
B
Q
Inputs Output
B A Q
0 0 0
0 1 0
1 0 0
1 1 1
The truth table for the 2
input AND gate
Symbol for a 2 input
AND gate
Q=A.B
Boolean expression for a 2
input AND gate
3 input AND gate:
A
B
Q
C
Inputs Output
C B A Q
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Symbol for a 3 input
AND gate
The truth table for the 3
input AND gate
Q=A.B.C
Boolean expression for a 3
input AND gate
CSC-103

8. The OR gate
2 input OR gate:
8
Inputs Output
B A Q
0 0 0
0 1 1
1 0 1
1 1 1
The truth table for the 2
input OR gate
Symbol for a 2 input
OR gate
Q = A + B
Boolean expression for a 2
input OR gate
3 input OR gate:
Inputs Output
C B A Q
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
Symbol for a 3 input
OR gate
The truth table for the 3
input OR gate
Q = A + B + C
Boolean expression for a 3
input OR gate
CSC-103

9. The NOT gate
Symbol for a NOT gate :
9
The truth table for the 2
input OR gate
Truth Table for NOT gate
A = A’
Boolean expression for NOT
gate
Input Output
A Q
0 1
1 0
This is the simplest form of logic
gate and has only 1 input and 1
output.
CSC-103

10. The NAND gate
2 input NAND gate:
10
Inputs Output
B A Q
0 0 1
0 1 1
1 0 1
1 1 0
The truth table for the 2
input NAND gate
Symbol for a 2 input
NAND gate
Q = A . B
Boolean expression for a 2
input NAND gate
3 input NAND gate:
Inputs Output
C B A Q
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 0
Symbol for a 3 input
NAND gate
The truth table for the 3
input NAND gate
Q = A . B . C
Boolean expression for a 3
input NAND gate
A
B
Q Q
A
B
C
CSC-103

11. The NOR gate
2 input NOR gate:
11
Inputs Output
B A Q
0 0 1
0 1 0
1 0 0
1 1 0
The truth table for the 2
input NOR gate
Symbol for a 2 input
NOR gate
Q = A + B
Boolean expression for a 2
input NOR gate
3 input NOR gate:
Inputs Output
C B A Q
0 0 0 1
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 0
Symbol for a 3 input
NOR gate
The truth table for the 3
input NOR gate
Q = A + B + C
Boolean expression for a 3
input NOR gate
A
B
Q
Q
A
B
C
CSC-103

12. The XOR gate
2 input XOR gate:
12
Inputs Output
B A Q
0 0 0
0 1 1
1 0 1
1 1 0
The truth table for the 2
input XOR gate
Symbol for a 2 input
XOR gate
Boolean expression for a 2
input XOR gate
A
B
Q
B
A
B
A
Q
or
B
A
Q
.
. 



CSC-103

13. The XNOR gate
2 input XNOR gate:
13
Inputs Output
B A Q
0 0 1
0 1 0
1 0 0
1 1 1
The truth table for the 2
input XNOR gate
Symbol for a 2 input
XNOR gate
Boolean expression for a 2
input XNOR gate
A
B
Q
B
A
B
A
Q
or
B
A
Q
.
. 



CSC-103

14. Universal Logic Gates
 NAND and NOR gates are referred to as universal gates as
the three basic gates can be constructed using either one of
the two.
 This therefore implies that all logic circuits can be
constructed using either of the gates.
 NAND and NOR gates are economical and easier to
implement.
14
CSC-103

15. Implementation of other gates using
Universal Logic Gates
15
Basic Gates Using NOR Gate Basic Gates Using NAND Gate
CSC-103

16. Exercise - 1.1
1. Look at the following logic symbols labeled A – G.
16
i. Which is the correct symbol for an AND gate. ……………
ii. Which is the correct symbol for a NOT gate. ……………
iii.Which is the correct symbol for a NOR gate. ……………
iv.Which is the correct symbol for an EXOR gate. ……………
v. Which is the correct symbol for a NAND gate. ……………
vi.Which is the correct symbol for an XNOR gate. ……………
vii.Which is the correct symbol for an OR gate. ……………
CSC-103

17. Exercise - 1.1 (Cont…)
2. Complete the following truth tables.
17
i. AND gate.
Inputs Output
B A Q
0 0
0 1
1 0
1 1
ii. NOR gate.
Inputs Output
B A Q
0 0
0 1
1 0
1 1
iii. XNOR gate.
Inputs Output
B A Q
0 0
0 1
1 0
1 1
iv. NAND gate.
Inputs Output
B A Q
0 0
0 1
1 0
1 1
v. OR gate.
Inputs Output
B A Q
0 0
0 1
1 0
1 1
CSC-103

18. Exercise - 1.1 (Cont…)
3. The Boolean equations labeled 1 – 9, below are to be used to answer the
following questions.
18
B
A
Q .

B
A
Q 

B
A
Q 

B
A
B
A
Q .
. 

B
A
Q 

B
A
B
A
Q .
. 

A
Q 
B
A
Q .

B
A
Q 

1.
2.
3.
4.
5.
6.
7.
8.
9.
i. Which expression is correct for an AND gate.……………
ii. Which expression is correct for a NOT gate.……………
iii. Which expression is correct for a NOR gate.……………
iv. Which two expressions are correct for an EXOR gate.……… & ………
v. Which expression is correct for a NAND gate.……………
vi. Which two expressions are correct for an XNOR gate.……… & ………
vii. Which expression is correct for an OR gate.……………
CSC-103

19. Equation to Circuit
To convert a Boolean expression to a gate circuit, evaluate
the expression using standard order of operations:
1. To solve the equation start from the left to right
2. Parentheses
3. Inverse (Not Gate)
4. Multiplication (AND Gate)
5. Addition (OR Gate)
19
CSC-103

20. Circuit to Equation
To convert a gate circuit to a Boolean expression, label each
gate output with a Boolean sub-expression corresponding
to the gates' input signals, until a final expression is
reached at the last gate.
20
The Expression for above circuit is XʹY+XYʹ.
CSC-103

21. Class Practice
1. Draw the circuit diagram for the equation
i. AB + (AC)ʹ.
ii. (A+B) . (B+C)
iii. (A+B+C) . B . C
2. Write down the corresponding Boolean expression for
following circuit.
21
CSC-103

22. Exercise – 1.2
1. Draw the corresponding circuit and truth table for
following Boolean expression
XYZ(YZ’+ZY’)
2. Draw a logic circuit and truth table for (A + B)C.
3. Find the Boolean expression and truth table for
following circuit.
22
CSC-103

23. Thank You
23
CSC-103