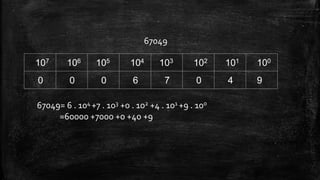
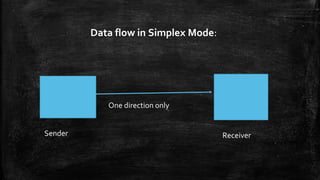
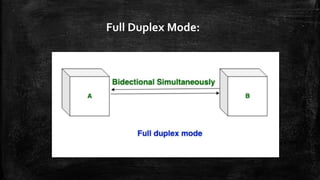
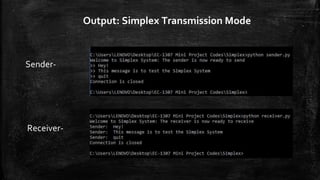
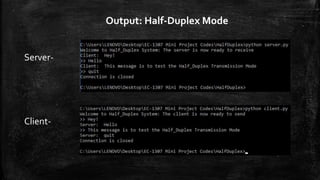
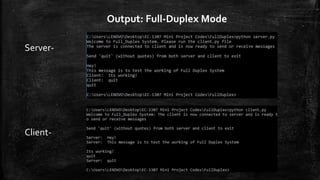
The document discusses topics related to data communication and networks, including data representation and direction of data flow. It explains various number systems (binary, decimal, octal, hexadecimal) and their conversions, as well as character data representation using ASCII and Unicode. Additionally, it outlines data flow types: simplex, half duplex, and full duplex with examples and Python code implementations for each mode.

1. DATA COMMUNICATION AND
NETWORKS
(EC 1307)
Mini Project

2. Topics:
Data representation (ASCII, ISO etc.), direction of data flow
(simplex, half duplex, full duplex)
Prepared by:
Sujit Kumar Nath, 17-1-4-006
Reddy Purna Teja, 17-1-4-007
Agasti Uday Shankar, 17-1-4-008
Disharna Das, 17-1-4-009
Gagan Harlalka, 17-1-4-010

3. DATA REPRESENTATION
▪ Data refers to the symbols that represent people, events, things, and ideas.
▪ Data can be a name, a number, the colors in a photograph, or the notes in
a musical composition.
▪ Data Representation refers to the form in which data is stored, processed, and
transmitted.

4. ▪ Digitization is the process of converting information, such as text,
numbers,photo, or music into digital data that can be manipulated
by electronic devices.
▪ The Digital Revolution has evolved through four phases, beginning
with big, expensive, standalone computers, and progressing to
today’s digital world in which small, inexpensive digital devices are
everywhere.

5. ▪ The 0s and 1s used to represent digital data are referred to as binary
digits. From this term we get the word bit that stands for binary digit.
▪ A bit is a 0 or 1 used in the digital representation of data.
▪ A digital file, usually referred to simply as a file, is a named collection of
data that exists on a storage medium, such as a hard disk, CD, DVD, or
flash drive.

6. Representing Numbers:
▪ Numeric data consists of numbers that can be used in arithmetic operations.
▪ Digital devices represent numeric data using the binary number system, also
called base 2.
▪ The binary number system only has two digits: 0 and 1.
▪ No numeral like 2 exists in the system, so the number “two” is represented in
binary as 10 (pronounced “one zero”).

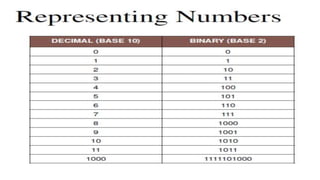
7. ● Base 10 (Decimal) - Represent any number using 10 digits [0-
9]
● Base 2 (Binary) - Represent any number using 2 digits [0-1]
● Base 8 (Octal) - Represent any number using 8 digits [0-7]
● Base 16 (Hexadecimal) - Represent any number using 10
digits and 6 characters [0-9, A, B, C, D, E, F]

9. ● The most common system for number representation is the
decimal.
● It’s used in finances, engineering and biology, almost everywhere
we see and use numbers
● As the name is saying the decimal number system is using 10
symbols/characters.
Decimal (base 10)

10. Characteristics Of Decimal Number System
● It uses 10 symbols
● Can be decomposed in factors containing powers of 10
● It’s the most common number representation system

11. Decimal Symbols
0 1 2 3 4 5 6 7 8 9
● As we can see there are 10 symbols from 0 to 9. With these
symbols we can construct all the numbers in the decimal
system.

12. ● All the numbers in the decimal system can be constructed by using
the symbols (0 … 9) multiplied with the power of 10. The power of 10
gives us ones, tens, hundreds, thousand and so on.
10K ... 105 104 103 102 101 100
N ... 10000
0
10000 1000 100 10 1

13. ● The example in the next slide breaks down the decimal number
67049 into powers of 10 multiplied with numbers between 0 and 9.
● This is to show that any number in the decimal system can be
decomposed into a sum of terms made of from the product of the
power of 10 and symbols 0 … 9.

14. 67049
107 106 105 104 103 102 101 100
0 0 0 6 7 0 4 9
67049= 6 . 104 +7 . 103 +0 . 102 +4 . 101 +9 . 100
=60000 +7000 +0 +40 +9

15. ● The same technique can be applied to the binary, octal and
hexadecimal systems, being in fact a method of converting a
number from decimal system in another format(base).

16. ❑ BASE OR RADIX
• The base of a number system (also called the radix ) is equal
to the number of digits used in the system.
Example :
• The decimal system uses the ten digits : 0 1 2 3 4 5 6 7 8 9 and
has a base of 10.
• The binary system uses two digits 01 and has a base of 2

17. THE BINARY NUMBER SYSTEM :
• A binary number is a sequence of the digits 0 and 1, such as
1101001.
• The number such as 1101001 has no fractional part and so is
called a binary integer.
• A binary number having a fractional part contains a binary
point (also called a radix point ),as in the number 1001.01

18. WRITING BINARY NUMBERS
A binary number is sometimes written with a subscript 2 when
there is a chance that the binary number would otherwise be
mistaken for a decimal number.
EXAMPLE:
• The binary number 110 could easily be mistaken for the
decimal number 110, unless we
write it 1102
• Similarly, a decimal number that may be mistaken for
binary is often written with a subscript
10, as in 10110

19. THE HEXADECIMAL NUMBER SYSTEM
• Hexadecimal numbers (or hex for short) are obtained by
grouping the bits in a binary number into sets of four and
representing each such set by a single number or letter.
• A hex number one-fourth the length of the binary number is
thus obtained.

20. ❑BASE 16:
• Since a 4 bit group of binary
digits can have a value between
0 and 15, we need 16 symbols to
represent all of these values.
• The base of hexadecimal
numbers is thus 16. We use the
digits from 0 to 9 and the capital
letters A to F, as shown in Table.

21. ❑ CONVERTING BINARY TO HEXADECIMAL
• To convert binary to
hexadecimal, we group the
bits into sets of four starting
at the binary point, adding
zeros as needed to fill out
the groups.
• Then we assign to each
group the appropriate letter
or number from Table 2
Example :
Convert 10110100111001 to hexadecimal
• Grouping, we get: 0010 1101 0011 1001
• Form table, we obtain 2 D 3 9
• So the hexadecimal equivalent is 2D39.

22. ❑CONVERTING HEXADECIMAL TO DECIMAL
• To convert from hex to decimal ,
we first replace each letter in the
hex number by its decimal
equivalent.
• Then we write the number in
expanded notation, multiplying
each hex digit by its place value.
• Finally, we add the resulting
numbers.
Example:
Convert the hex number 3B.F to
decimal
• First, We replace the hex B with 11,
and the hex F with 15, and write
the number in expanded form.

23. ❑CONVERTING DECIMAL TO HEXADECIMAL
• To convert decimal to
hexadecimal, we repeatedly
divide the given decimal
number by 16 and convert
each remainder to hex.
• The remainders form our
hex number, the last
remainder obtained being
the most significant digit.
Example:
Convert the decimal number 83759 to
hex
• Changing the number 15 to hex F and
reading the remainders from bottom
up, we find that our hex equivalent is
1472F.
Readup

24. THE OCTAL NUMBER SYSTEM:
• The octal number system
uses eight digits, 0 to 7, and
hence has a base of eight.
• A comparison of the decimal,
binary, hex, and octal digits is
given in Table

25. ❑ BINARY-OCTAL CONVERSIONS
• To convert from binary to octal,
we write the bits of the binary
number in groups of three,
starting at the binary point.
• Then we write the octal
equivalent for each group.
Example:
Convert the binary number
1101000110110 to octal.
• Grouping the bits in sets of three
from the binary point, we obtain:
001 101 000 110 110
• And the octal equivalent:1 5 0 6 6

26. Representing Text:
▪ Character data is composed of letters, symbols, and
numerals that are not used in calculations.
▪ Examples of character data include our name, address, and
hair color.
▪ Character data is commonly referred to as “text.”

27. • In data communications, text is represented as a bit pattern, a
sequence of bits (0’s or 1’s).
• Different sets of bit patterns have been designed to represent
text symbols.

28. Different Formats of Character Data:
Digital devices employ several types of codes to represent
character data,including ASCII, Unicode, and their variants.
These codes have been discussed in the subsequent slides.

29. ▪ The American Standard Code for Information Interchange (ASCII),
developed some decades ago in the United States, now constitutes the first
127 characters in Unicode and is also referred to as Basic Latin.
▪ It requires seven bits for each character.
▪ For example, the ASCII code for an uppercase A is 1000001.
ASCII Format of data:

30. ▪ ASCII codes are used for numerals, such as Social Security numbers
and phone numbers.
▪ Plain, unformatted text is sometimes called ASCII text and is stored
in a so-called text file with a name ending in .txt.
▪ On Apple devices these files are labeled “Plain Text.” In Windows,
these files are labeled “Text Document”.
▪ ASCII text files contain no formatting

31. • Extended ASCII is a superset of ASCII that uses eight bits for each
character.
• For example, Extended ASCII represents the uppercase letter A as
01000001.
• Using eight bits instead of seven bits allows Extended ASCII to
provide codes for 256 characters.

32. Unicode format of data:
▪ Unicode (pronounced “YOU ni code”) uses sixteen bits and
provides codes or 65,000 characters.
▪ This is a bonus for representing the alphabets of multiple
languages.
▪ UTF-8 is a variable-length coding scheme that uses seven bits
for common ASCII characters but uses sixteen-bit Unicode as
necessary.

33. ▪ Unicode was originally a 2-byte character set.
▪ Unicode version 3, however, is a 4-byte code and is fully
compatible with ASCII and Extended ASCII.
▪ The ASCII set, which is now called Basic Latin, is Unicode with
the upper 25 bits set to zero.

34. • Extended ASCII, which is now called Latin-1, is Unicode with the
24 upper bits set to zero.
• The fig shows how the different systems are compatible.
Unicode Compatibility

35. UTF-32:
The prevalent code today is UTF-32. Each character or
symbol in this code is defined by a 32-bit number.
The code can define up to 232 (4,294,967,296) characters
or symbols.

36. • The notation uses hexadecimal digits in the following format: U-
XXXXXXXX
• Each X is a hexadecimal digit. Therefore, the numbering goes from
U-00000000 to U-FFFFFFFF.

37. Planes :
▪ Unicode divides the available space codes into planes.
▪ The most significant 16 bits define the plane, which means
we can have 65,535 planes.
▪ Each plane can define up to 65,536 character or symbols.

38. Direction of Data Flow
There are three types of direction of data flow:
1. Simplex
1. Half Duplex
1. Full Duplex

39. Simplex Data Flow:
● In Simplex Data Flow, sender can send information in one
direction only.
● Sender can send the data but that sender can’t receive the
data. Similarly, the receiver can only receive the data, but
cannot send it.

40. ● It is the simplest form in communication.
● The simplex mode provides less
performance than half duplex and full
duplex.

41. Example of Simplex Data Flow:
1. Keyboard: The keyboard can only introduce input
1. Monitor: The monitor can only give the output

42. Data flow in Simplex Mode:
Sender Receiver
One direction only

43. Half Duplex Data Flow
● In half duplex mode, Sender can send the data and also
can receive the data but one at a time
● It is two-way directional communication but one at a
time.

44. Half Duplex Mode:

45. ● The half-duplex mode is used in cases where there
is no need for communication in both direction at
the same time.
● The entire capacity of the channel can be utilized
for each direction.

46. Example of Half Duplex Mode:
Walkie-Talkies:
● Typical walkie-talkies resemble a telephone handset,
with a speaker built into one end and a microphone in
the other (in some devices the speaker also is used as
the microphone) and an antenna mounted on the top
of the unit. They are held up to the face to talk.
● A walkie-talkie is a half-duplex communication device.
Multiple walkie-talkies use a single radio channel, and
only one radio on the channel can transmit at a time,
although any number can listen

47. Full Duplex Data Flow
● In full duplex mode, Sender can send the data and also
can receive the data simultaneously
● It is two-way directional communication simultaneously.

48. In full duplex mode, signals going in one direction share the
capacity of the link with signals going in other direction, this
sharing can occur in two ways:
1. Either the link must contain two physically separate
transmission paths, one for sending and other for receiving.
1. Or the capacity is divided between signals travelling in both
directions.

49. ● Full-duplex mode is used when communication
in both direction is required all the time.
● The capacity of the channel, however must be
divided between the two directions.

50. Full Duplex Mode:

51. Example of Full Duplex:
● Telephone Network in which there is communication
between two persons by a telephone line, through
which both can talk and listen at the same time.

52. Codes and Results
Python Code for the following are attached along with the
presentation:
1. Decimal Conversion( to Binary, Octal and Hexadecimal)
1. Simplex Transmission Mode
1. Half-Duplex Transmission Mode
1. Full-Duplex Transmission Mode

53. Decimal Conversion
The Python code takes a decimal number as input, and
produces the Binary, Octal, and Hexadecimal form of the
number
Output:

54. Simplex Transmission Mode
The python files- sender.py and receiver.py create 2 sockets -
one for sender, and the other for receiver. The sender can only
send messages, while the receiver can only receive the
messages
Thus the goal of a Simplex Transmission Mode is achieved

55. Output: Simplex Transmission Mode
Sender-
Receiver-

56. Half Duplex Transmission Mode
The python files- client.py and server.py create 2 sockets -
one for the client, and other for the server, to which the
client is connected to. Both the server and the client can
send messages to one another, but only one at a time.
Thus the goal of a Half Duplex Transmission Mode is
achieved

57. Output: Half-Duplex Mode
Server-
Client-

58. Full Duplex Transmission Mode
The python files- client.py and server.py create 2 sockets -
one for the client, and other for the server, to which the
client is connected to. Both the server and the client can
send messages to one another simultaneously, with no
restrictions.
Thus the goal of a Full Duplex Transmission Mode is achieved

59. Output: Full-Duplex Mode
Server-
Client-

60. Thank You