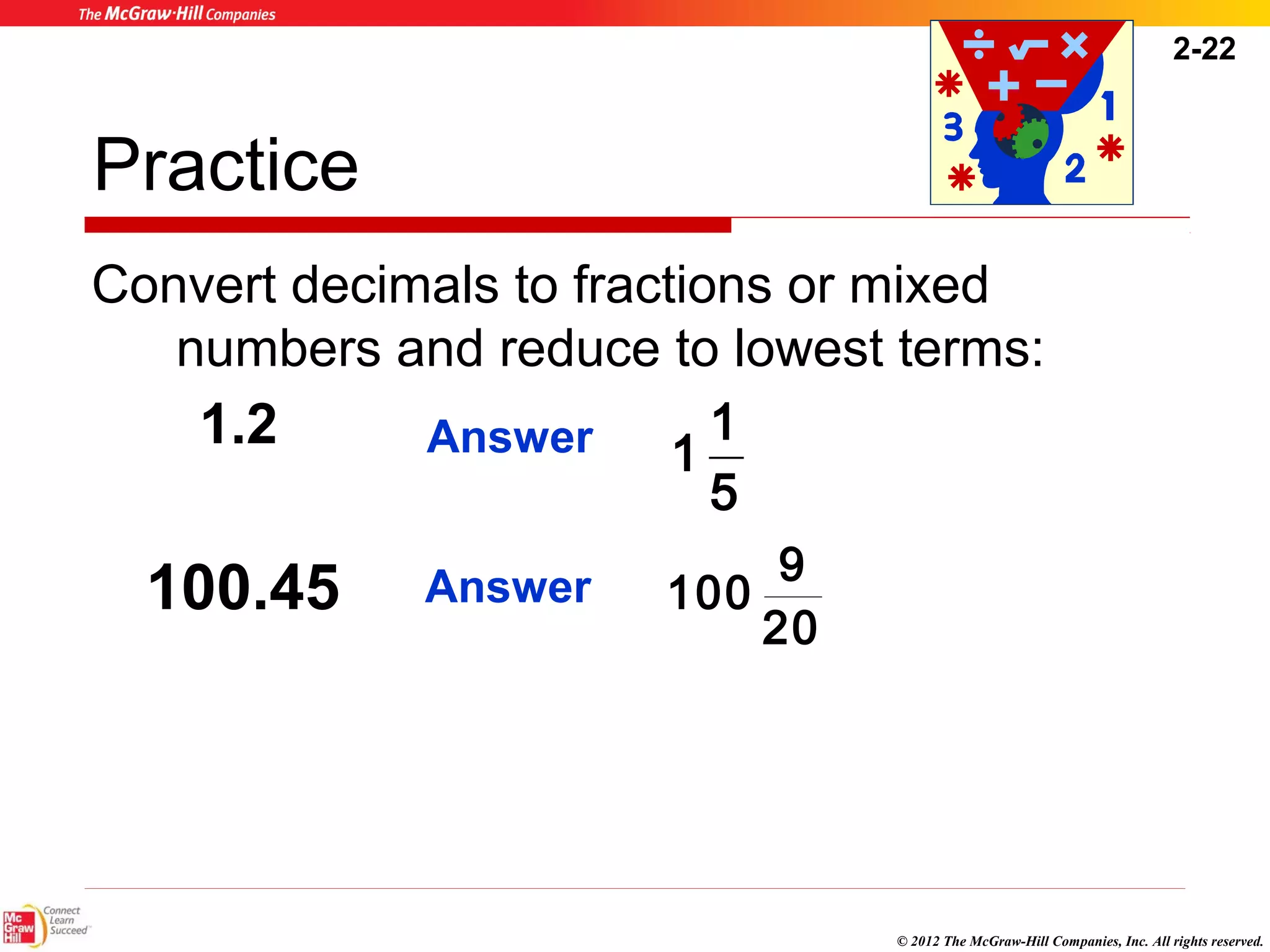
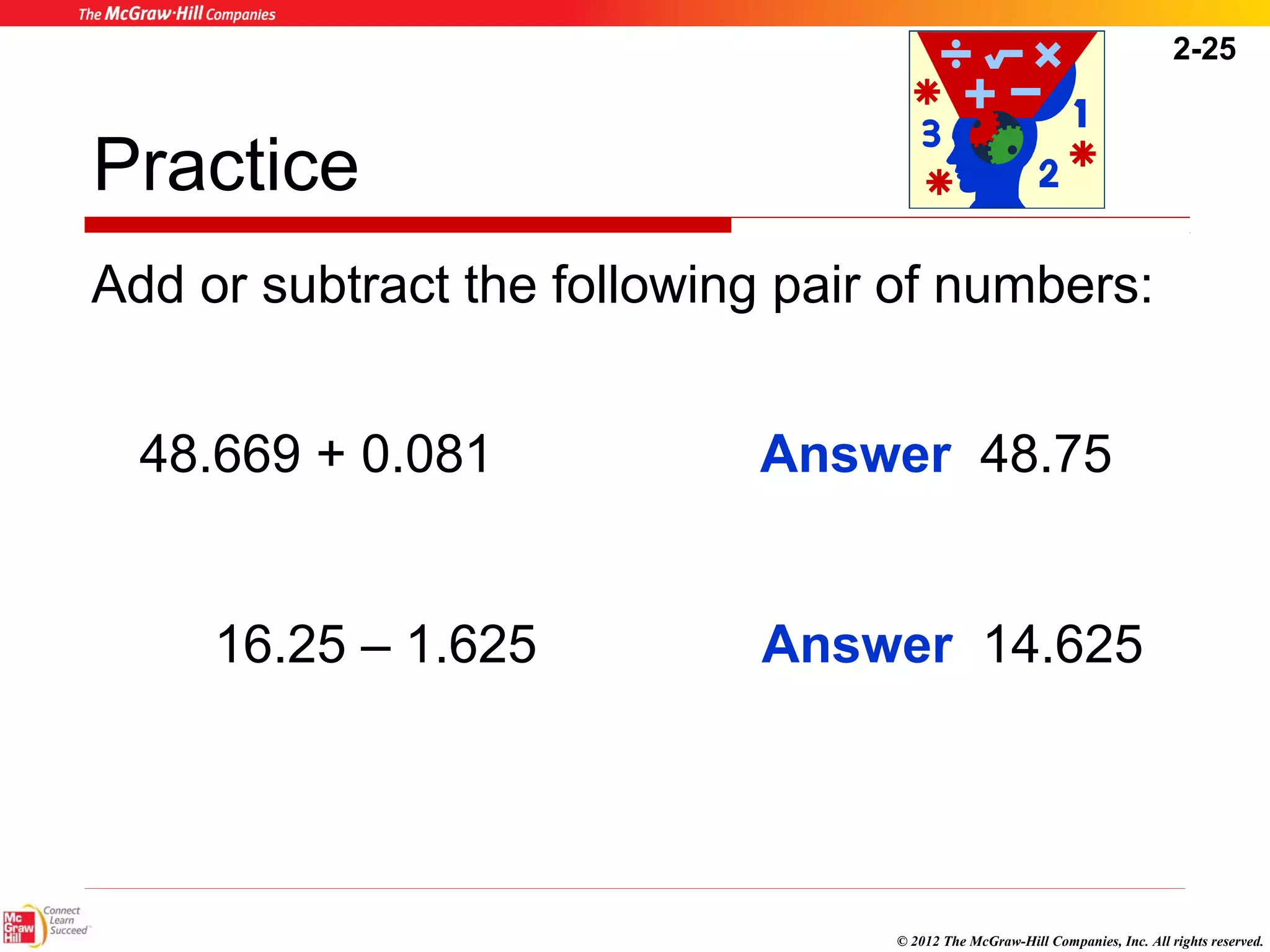
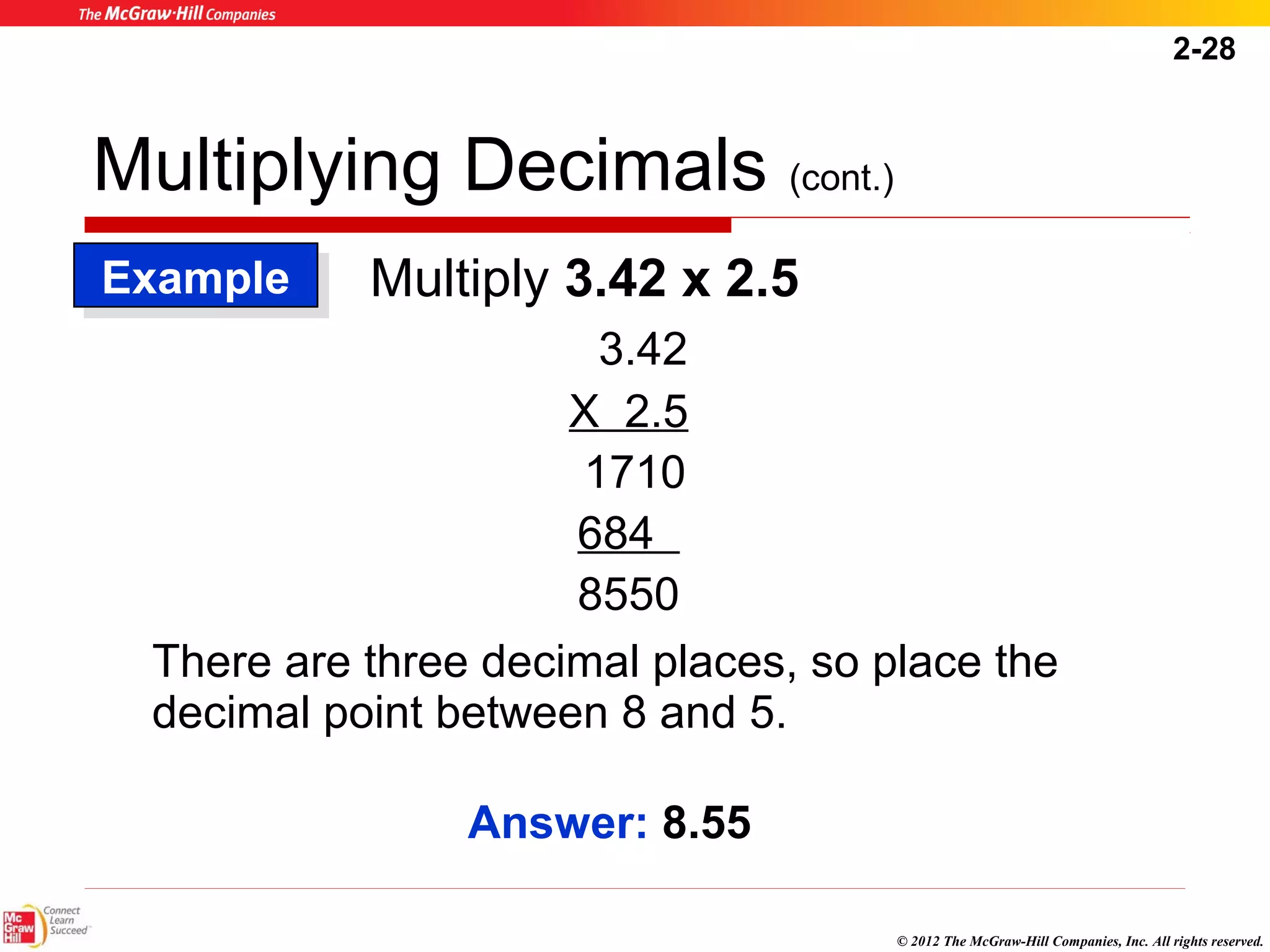
This document summarizes key concepts from Chapter 2 of a textbook on decimals. It discusses writing, comparing, rounding, and converting decimals and fractions. Arithmetic operations like addition, subtraction, multiplication and division of decimals are also covered. Examples and practice problems are provided to illustrate the rules and steps for working with decimals. The goal is to help healthcare professionals feel comfortable using decimals for dosage calculations.

1. Chapter 2 Decimals
PowerPoint® Presentation to accompany:
Math and Dosage Calculations
for Healthcare Professionals
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Fourth Edition
Booth, Whaley, Sienkiewicz, and Palmunen

2. 2-2
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Learning Outcomes
2-1 Write decimals and compare their value.
2-2 Apply the rules for rounding decimals.
2-3 Convert fractions into decimals.
2-4 Convert decimals into fractions.

3. 2-3
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Learning Outcomes (cont.)
2-5 Add and subtract decimals.
2-6 Multiply decimals.
2-7 Divide decimals.

4. 2-4
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Key Terms
 Divisor
 Dividend
 Quotient

5. 2-5
Introduction
 Many of the math skills used for fractions
are used for numbers containing decimals.
 It is important to be comfortable working
with decimals when performing dosage
calculations.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

6. 2-6
Decimals
 Decimals are another way to represent
whole numbers and their fractional parts.
 They are used daily by Healthcare
practitioners.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
 The Metric System
 is decimal based;
 is used in dosage calculations, calibrations, and
charting.

7. 2-7
 The location of a digit relative to the
decimal point determines its value.
 The decimal point separates the whole
number from the decimal fraction.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Decimals (cont.)

8. 2-8
Decimals (cont.)
Decimal Place Values
The number 1,542.567 can be represented as follows:
Whole Number Decimal
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Point
Decimal Fraction
Thousands Hundreds Tens Ones . Tenths Hundredths Thousandths
1, 5 4 2 . 5 6 7

9. 2-9
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Decimal (cont.)
The number 1,542.567 is read:
(1) – one thousand
(5) – five hundred
(42) – forty two and
(0.5) – five hundred
(0.067) – sixty-seven thousandths
One thousand five hundred forty two and five
hundred sixty-seven thousandths

10. 2-10
Writing Decimals
RRuullee 22--11 When writing a decimal number:
1. Write the whole number part to the left
of the decimal point.
2. Write the decimal fraction part to the
right of the decimal point.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

11. 2-11
Writing Decimals
RRuullee 22--11 When writing a decimal number:
3. Use zero as a placeholder to the right of
the decimal point.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
 Example: 0.201

12. 2-12
Writing Decimals (cont.)
RRuullee 22--22 Always write a zero to the left of
the decimal point when the decimal
number has no whole number part.
 This helps to prevent errors caused by
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
illegible handwriting.

13. 2-13
Comparing Decimals
RRuullee 22--33 To compare values of a group of
decimal numbers:
1. The decimal with the greatest whole number is
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
the greatest decimal number.
2. If the whole numbers are equal, compare the
digits in the tenths place.

14. 2-14
Comparing Decimals
RRuullee 22--33 To compare values of a group
of decimal numbers: (cont.)
3. If the tenths place digits are equal, compare
the hundredths place digits.
4. Continue moving to the right comparing digits
until one is greater than the other.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

15. 2-15
Comparing Decimals (cont.)
 The more places a number is to the right of
the decimal point the smaller the number’s
value.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
3
EExxaammpplleess
0.3 is or three tenths
10
3
0.03 is or three hundredths 100
3
0.003 is 1 0 0 0 or three thousandths

16. 2-16
Answers = 0.2
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Practice
Write the following in decimal form:
2
10
17
100
23
1000
= 0.17
= 0.023

17. 2-17
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Rounding Decimals
RRuullee 22--44
1. Underline the place value.
2. Look at the digit to the right of this target.
3. Drop all digits to the right of the target place
value.

18. 2-18
Answer 8.80
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Practice
Round to the nearest tenth:
14.34
9.293
Answer 14.3
Round to the nearest hundredth:
8.799
10.542
Answer 9.3
Answer 10.54

19. 2-19
Converting Fractions into
Decimals
RRuullee 22--55
To convert a fraction to a decimal, divide the
numerator by the denominator.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
0.75
3 =
4
1.6
8 =
5
EExxaammppllee

20. 2-20
Converting Decimals into
Fractions (cont.)
RRuullee 22--66
1. Write the number to the left of the decimal
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
point as the whole number.
2. Write the number to the right of the decimal
point as the numerator of the fraction.

21. 2-21
Converting Decimals into
Fractions (cont.)
RRuullee 22--66 (cont.)
3. Use the place value of the digit farthest to the
right of the decimal point as the denominator.
3. Reduce the fraction part to its lowest term.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

22. 2-22
Practice
Convert decimals to fractions or mixed
numbers and reduce to lowest terms:
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
1.2 Answer
100.45
1 1 or
5
Answer
100 9 or
20

23. 2-23
Adding and Subtracting
Decimals
RRuullee 22--77
1. Write the problem vertically. Align the decimal
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
points.
2. Add or subtract starting from the right. Include
the decimal point in your answer.
2.47
+ 0.39
2.86

24. 2-24
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Adding and Subtracting
Decimals (cont.)
Subtract
7.3 – 1.005
Answer:
7.300
- 1.005
6.295
Add
13.561 + 0.099
Answer:
13.561
+ 0.099
13.660
EExxaammpplleess

25. 2-25
Practice
Add or subtract the following pair of numbers:
Answer 48.75
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
48.669 + 0.081
Answer 14.625
16.25 – 1.625

26. 2-26
Multiplying Decimals
RRuullee 22--88 (cont.)
1. First, multiply without considering the decimal
points, as if the numbers were whole
numbers.
2. Count the total number of places to the right
of the decimal point in both factors.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

27. 2-27
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Multiplying Decimals
RRuullee 22--88 (cont.)
3. To place the decimal point in the product,
start at its right end and move the it to the left
the same number of places.

28. 2-28
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Multiplying Decimals (cont.)
EExxaammppllee
Multiply 3.42 x 2.5
3.42
X 2.5
1710
684
8550
There are three decimal places, so place the
decimal point between 8 and 5.
Answer: 8.55

29. 2-29
Practice
A patient is given 7.5 milliliters of liquid medication 5
times a day. How may milliliters does she receive
per day?
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Answer 7.5 x 5
7.5
X 5
37.5

30. 2-30
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Dividing Decimals
RRuullee 22--99
1. Move the decimal point to the right the same
number of places in both the divisor and
dividend until the divisor is a whole number.

31. 2-31
Dividing Decimals
RRuullee 22--99 (cont.)
2. Complete the division as you would with whole
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
numbers.
 Align the decimal point of the quotient with the
decimal point of the numerator.

32. 2-32
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Dividing Decimals (cont.)
EExxaammppllee Divide
0.066 ¸ 0.11
(1) 0.066 ¸0.11 (2) 6.6 ¸ 11
( )
0.6
3 11 6.6
0.066 ¸ 0.11 = 0.6

33. 2-33
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Practice
A bottle contains 32 ounces of medication. If the
average dose is 0.4 ounces, how many doses
does the bottle contain?
Answer: 80

34. 2-34
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
In Summary
 In this chapter you learned to:
 write decimals and compare their value;
 apply rules for rounding decimals;
 convert fractions to decimals.

35. 2-35
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
In Summary (cont.)
 In this chapter you learned to:
 convert decimals into fractions;
 add and subtract decimals;
 multiply decimals;
 divide decimals.

36. 2-36
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Apply Your Knowledge
Round to the nearest tenth:
7.091
Answer 7.1

37. 2-37
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Apply Your Knowledge
Add the following: 7.23 + 12.38
Answer 19.61
Multiply the following: 12.01 x 1.005
Answer 12.07005

38. 2-38
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
End of Chapter 2
Learning is not
attained by
chance,
it must be sought
for with ardor
and attended to
with diligence.
-Abigail Adams