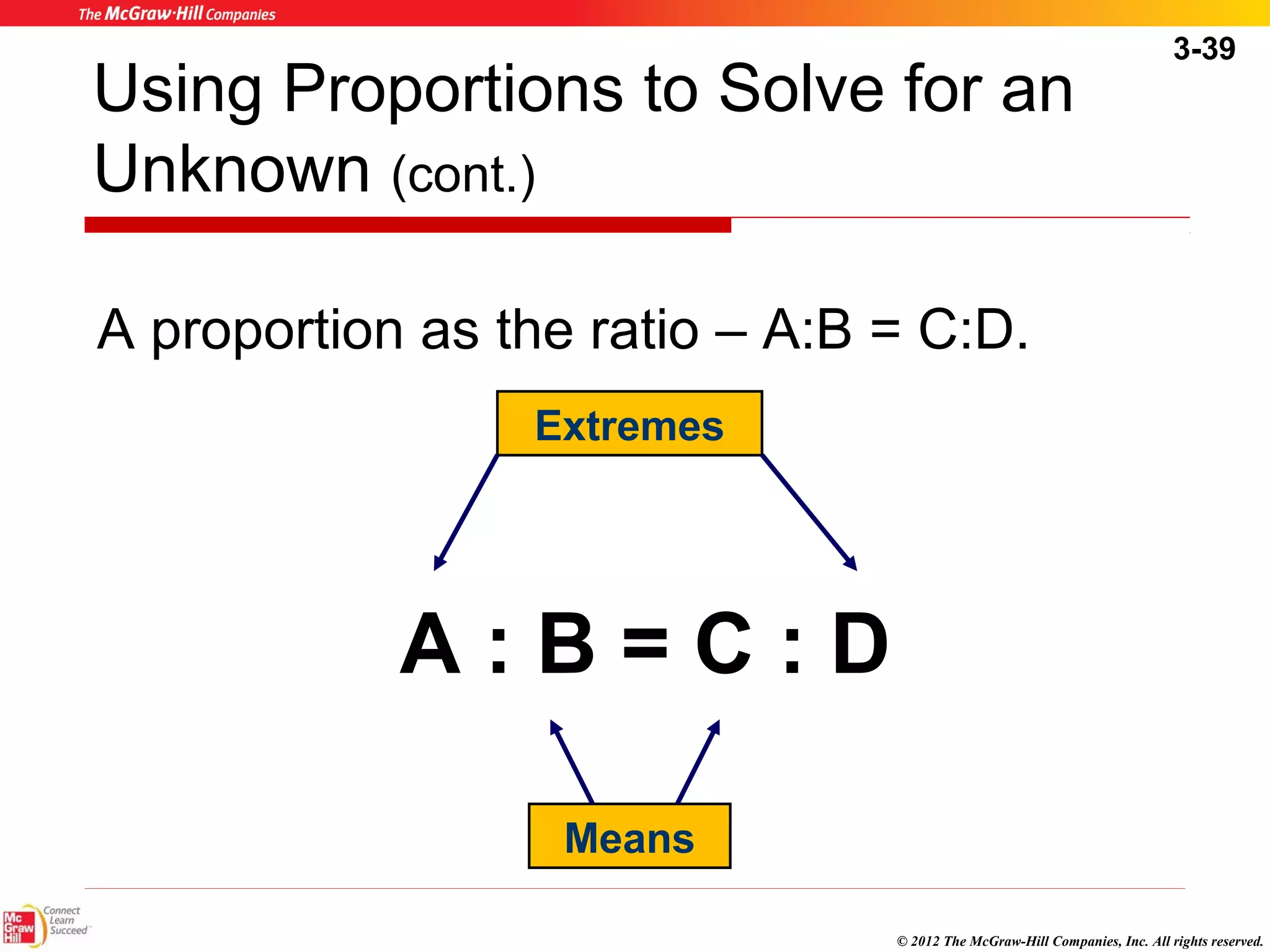
This document summarizes key concepts about ratios, proportions, and percents from Chapter 3 of a textbook on math and dosage calculations for healthcare professionals. It defines important terms like ratio, proportion, and percent. It provides rules and examples for converting between ratios, proportions, percents, fractions and decimals. It also explains how to use proportions to solve for unknown quantities, including setting up equations and checking solutions. The overall purpose is to explain essential skills for understanding relationships between quantities and solving dosage calculation problems.

1. Chapter 3
Relationships of Quantities:
Percents, Ratios, and Proportions
PowerPoint® Presentation to accompany:
Math and Dosage Calculations for
Healthcare Professionals
Fourth Edition
Booth, Whaley, Sienkiewicz, and Palmunen
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

2. 3-2
Learning Outcomes
3-1 Convert values to and from a percent.
3-2 Convert values to and from a ratio.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
3-3 Write proportions.
3-4 Use proportions to solve for an unknown
quantity.

3. 3-3
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Key Terms
 Cross-multiplying
 Means and
extremes
 Percent
 Proportion
 Ratio

4. 3-4
Introduction
 For dosage calculation you must:
 understand percents, ratios, and
proportions ;
 be able to find a unknown quantity in a
proportion.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

5. 3-5
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Percents
 Percents provide a way to express the
relationship of parts to a whole.
 Percent is indicated by the symbol %.
 Percent means “per 100” or “divided by 100.”

6. 3-6
Percents (cont.)
 A number < 1 is expressed as less than
100 percent.
 A number > 1 is expressed as greater than
100 percent.
 Any expression of one equals 100 percent.
1.0 = = 100 percent
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
5
5

7. 3-7
Converting Values To and From a
Percent
RRuullee 33--11
To convert a percent to a decimal, remove
the percent symbol. Then divide the
remaining number by 100.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

8. 3-8
Converting Values To and From
a Percent (cont.)
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
EExxaammppllee
Convert 42% to a decimal:
 Move the decimal point two places to the left.
 Insert the zero before the decimal point for clarity.
 42% = 42.% = .42. = 0.42

9. 3-9
RRuullee 33--22
To convert a decimal to a percent, multiply
the decimal by 100. Then add the
percent symbol.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Converting Values To and
from a Percent (cont.)

10. 3-10
Working with Percents (cont.)
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
EExxaammppllee
Convert 0.02 to a percent:
 Multiply by 100%.
 0.02 x 100% =2.00% = 2%

11. 3-11
Working with Percents (cont.)
RRuullee 33--33
To convert a percent to an equivalent
fraction, write the value of the percent as the
numerator and 100 as the denominator.
Then reduce the fraction to its lowest term.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

12. 3-12
Working with Percents (cont.)
Convert 8% to an equivalent fraction.
8% =
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
EExxaammppllee
2
25
8 = 8
=
100
100
2
25

13. 3-13
Converting Values To and from a
Percent (cont.)
RRuullee 33--44 To convert a fraction to a
percent:
1. convert the fraction to a decimal;
2. round to the nearest hundredth;
3. then follow the rule for converting a
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
decimal to a percent.

14. 3-14
Converting Values To and from a
Percent (cont.)
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
EExxaammppllee
Convert 2/3 to a percent.
 Convert 2/3 to a decimal and round to the
nearest hundredth.
 2/3 = 2 divided by 3 = 0.666 = 0.67
 0.67 x 100% = 67%

15. 3-15
Answer = 75%
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Practice
Convert the
following percents
to decimals:
Convert the
following
fractions to
percents:
Answer = 0.14
14%
300% Answer = 3.00
6/8
4/5 Answer = 80%

16. 3-16
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Ratios
 The relationship of a part to the whole
 relates a quantity of liquid drug to a quantity
of solution;
 is used to calculate dosages of dry
medication such as tablets.

17. 3-17
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Ratios (cont.)
 Like a fraction, a ratio has two parts.
 The first part = numerator.
 The second part = denominator.
 The two parts are separated by a colon.

18. 3-18
Converting Values To and
From a Ratio
RRuullee 33--55
Reduce a ratio as you would a fraction.
Reduce 2:12 to its lowest terms.
Both values 2 and 12 are divisible by 2.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
2:12 is written 1:6
EExxaammppllee

19. Converting Values To and
From a Ratio. (cont.)
RRuullee 33--66
To convert a ratio to a fraction, write value A (1st
3-19
number) as the numerator and value B (2nd
number) as the denominator, so that A:B =
Convert the following ratio to a
fraction:
A
4
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
4:5 =
B
5
EExxaammppllee

20. 3-20
Converting Values To and
From a Ratio.(cont.)
RRuullee 33--77
To convert a fraction to a ratio, write the
numerator as the 1st value A and the
denominator as the 2nd value B.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
A
= A:B B

21. 3-21
Converting Values To and
From a Ratio (con’t)
Convert the following into a ratio:
11
3 = 47:12
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
7
12 = 7:12
12
EExxaammppllee
47
=
12

22. 3-22
Converting Values To and
From a Ratio. (cont.)
RRuullee 33--88 To convert a ratio to a decimal:
1. write the ratio as a fraction;
2. convert the fraction to a decimal.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

23. 3-23
Converting Values To and From
a Ratio (cont.)
Convert the ratio 1:10 to a decimal.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
1. Write the ratio as a fraction.
1
1:10 = 10
EExxaammppllee
2. Convert the fraction to a decimal.
1
10
= 1 divided by 10 = 0.1
1 = 0.1
Thus, 1:10 = 10

24. 3-24
Converting Values To and
From a Ratio (cont.)
RRuullee 33--99 To convert a decimal to a ratio:
1. write the decimal as a fraction;
2. reduce the fraction to lowest terms;
3. restate the fraction as ratio.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

25. 3-25
Converting Values To and From a
Ratio (cont.)
1. Write the decimal 0.25 as a fraction.
25
100
2. Reduce the fraction to lowest terms.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
1
25
3. Restate the number as a ratio.
1:4
4
100
=
EExxaammppllee

26. 3-26
Converting Values To
and From a Ratio (cont.)
RRuullee 33--1100 To convert a ratio to a percent:
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
1. convert the ratio to a decimal;
2. write the decimal as a percent by multiplying
the decimal by 100 and adding the %
symbol.

27. 3-27
Converting Values To and
From a Ratio (cont.)
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Convert 2:3 to a percent.
1. 2:3 =
2 = 0.67
3
2. 0.67 X 100% = 67%
EExxaammppllee

28. 3-28
Converting Values To and From
a Ratio (cont.)
RRuullee 33--1111 To convert a percent to a ratio:
1. write the percent as a fraction;
2. reduce the fraction to lowest terms;
3. write the fraction as a ratio.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
 Numerator = value A
 Denominator = value B
 A:B

29. 3-29
Converting Values To and
From a Ratio (cont.)
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Convert 25% to a ratio.
1. 25% =
25
100
2. 25 = = =
1 : 4 25%
1
4
100
EExxaammppllee

30. 3-30
Practice
Convert the following ratios to a fraction or mixed
numbers:
3:4 5:3
1 2
5 =
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Answer =
3
4
Answer =
3
3

31. 3-31
Practice
Convert the following decimals to ratios:
0.9 8
Answer = 9 : 10
8 =
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
9 =
10
Answer = 8 : 1
1

32. 3-32
Writing Proportions
 A proportion is a mathematical statement that
two ratios or two fractions are equal.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
 2:3 is read “two to three”
 2:3 = 4:6 is read “two is to three as four is to
six”

33. 3-33
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Writing Proportions (cont.)
RRuullee 33--1122
To change a proportion from
ratios to fractions, convert both
ratios to fractions.

34. 3-34
50
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Writing Proportions (cont.)
Write 5:10 = 50:100 as a proportion using
fractions.
100
5
5:10 = 50:100 same as =
10
EExxaammppllee

35. 3-35
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Writing Proportions (cont.)
RRuullee 33--1133
To change a proportion from
fractions to ratios, convert each
fraction to a ratio.

36. 3-36
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Writing Proportions (cont.)
10
5 =
Write using ratios.
12
6
10 : 12
5 : 6 10
12
6 5
= and =
5:6 = 10:12
EExxaammppllee

37. 3-37
Write the following as proportions using
fractions:
10
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Practice
4:5 = 8:10 Answer
50:25 = 10:5
8
10
4 =
5
Answer
5
50 =
25

38. 3-38
Using Proportions to Solve for
an Unknown
 Proportions are used to calculate
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
dosages.
 If three of four of the values of a proportion
are known, the unknown quantity can be
determined by using:
 ratios; or
 fractions.

39. 3-39
Using Proportions to Solve for an
Unknown (cont.)
A proportion as the ratio – A:B = C:D.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Extremes
A : B = C : D
Means

40. 3-40
Using Proportions to Solve for an
Unknown (cont.)
RRuullee 33--1144 To determine if a proportion is
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
true:
1. multiply the means;
2. multiply the extremes;
3. compare the product of the means and the
product of the extremes.

41. 3-41
Using Proportions to Solve for an
Unknown (cont.)
Is 1:2=3:6 a true proportion?
1. Multiply the means: 2 X 3 = 6
2. Multiply the extremes: 1 X 6 = 6
3. Compare the products of the means and the
extremes: 6=6
1:2=3:6 is a true proportion.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
EExxaammppllee

42. 3-42
Using Proportions to Solve for an
Unknown (con’t)
RRuullee 33--1155 To find the unknown quantity in
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
a proportion:
1. Write an equation:
product of the means = product of the
extremes
2. Solve for the unknown quantity.

43. 3-43
Using Proportions to Solve for
an Unknown (con’t)
RRuullee 33--1155 (cont.)
3. Restate the proportion, inserting the unknown
quantity.
3. Check your work. Determine if the ratio
proportion is true.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

44. 3-44
Using Proportions to Solve for an
Unknown (cont.)
Find the unknown quantity in 25:5=50:x
250 x = x = 10
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
1. Write the equation:
5 x 50 = 25 X x becomes 250 = 25x
1. Solve the equation by dividing both sides by
25.
25
25
25
EExxaammppllee

45. 3-45
Using Proportions to Solve for
an Unknown (cont.)
EExxaammppllee ((ccoonntt..))
3. Restate the proportion, inserting the
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
unknown quantity. 25:5=50:10
3. Check your work.
5 X 50 = 25 X 10
250 = 250
The unknown quantity is 10.

46. 3-46
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
EERRRROORR AALLEERRTT!!
 Do not forget the units of measurement.
 Including units in the dosage strength will help
you avoid errors.

47. 3-47
Canceling Units in Proportions
(cont.)
RRuullee 33--1166
1. If the units in the first part of the ratio in
a proportion are the same, they can be
canceled.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

48. 3-48
Canceling Units in Proportions
(cont.)
RRuullee 33--1166 (cont.)
2. If the units in the second part of the ratio
in a proportion are the same, they can
be canceled.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

49. 3-49
Canceling Units in Proportions
(cont.)
If 100 mL of solution contains 20 mg of
drug, how many milligrams of the drug will
be in 500 mL of the solution?
20 mg:100 mL=x:500 mL 20mg X 500 = 100 X x
x = 100mg
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
10000 mg x =
100 X
100
100
EExxaammppllee

50. 3-50
Practice
Determine whether the following proportions
6:12=12:24 Answer = True
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
are true:
3:8=9:32
Answer = Not true

51. 3-51
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Practice
Use the means and extremes to find the
unknown quantity.
10:4=20:x Answer = 8
3:12=x:36
Answer = 9

52. 3-52
Using Proportions to Solve for an
Unknown (cont.)
RRuullee 33--1177 To determine if a proportion written
C
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
as fractions is true:
1. Cross-multiply
A =
1. Compare the products. The products must
be equal.
D
B

53. 3-53
Using Proportions to Solve for
an Unknown (cont.)
2 =
Determine if 2 5 is a true proportion.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
10
5
1. Cross-multiply. 2 X 25=5 X 10
2. Compare the products on both sides of the
equal sign. 50 = 50
2 Therefore, =
10
5
25 is a true proportion.
EExxaammppllee

54. 3-54
Using Proportions to Solve for
an Unknown (cont.)
RRuullee 33--1188 To find the unknown quantity
in a proportion written as fractions:
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
1. Cross-multiply.
 Write an equation setting the products equal to
each other.
2. Solve the equation to find the unknown
quantity.

55. 3-55
Using Proportions to Solve for
an Unknown (cont.)
RRuullee 33--1188 (cont.)
3. Restate the proportion, inserting the unknown
quantity.
3. Check your work.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

56. 3-56
Using Proportions to Solve for
an Unknown (cont.)
Find the unknown quantity in
6
x
3 =
5
EExxaammppllee
1. Cross-multiply.
3 X x = 5 X 6
2. Solve the equation by dividing both sides by
three.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
30
3 x = 10
3 X x =
3

57. 3-57
Using Proportions to Solve for
an Unknown (cont.)
EExxaammppllee ((ccoonntt.).)
3. Restate the proportion, inserting the unknown
quantity.
6
10
3
=
5
4. Check your work by cross-multiplying.
3 X 10 = 5 X 6
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
30 = 30
The unknown quantity is 10.

58. 3-58
Using Proportions to Solve for an
Unknown (cont.)
RRuullee 33--1199
If the units of the numerator of the two
fractions are the same, they can be
dropped or canceled before setting up a
proportion.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
10mg X ?
10
75mg
10mL
=

59. 3-59
Using Proportions to Solve for
an Unknown (cont.)
RRuullee 33--1199 (cont.)
Likewise, if the units from the denominator
of the two fractions are the same, they
can be canceled.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
5 ?
5mL
25mg =
5mL

60. 3-60
Using Proportions to Solve for an
Unknown (cont.)
You have a solution containing
200mg drug in 5mL. How many
milliliters of solution contain
500mg drug?
mg
mg 500
5
x
200 =
mL
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
EExxaammppllee
Set up the fractions.
Cross-multiply to solve the equation.

61. 3-61
Using Proportions to Solve for an
Unknown (cont.)
If 100 mL of solution contains 20mg of
drug, how many milligrams of the drug
will be in 500mL of solution?
mg x
mL mL
100 500
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
EExxaammppllee
Set up the fraction. 20 =
Cross-multiply to solve the equation.

62. 3-62
Practice
Determine if the following proportions are true:
Answer = Not true
Answer = Not true
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
28
48
7 =
16
125
300
50 =
125

63. 3-63
Practice
Cross-multiply to find the unknown quantity.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Answer = 1
Answer = 2
3 x =
15 5
25 = 75 x
6

64. 3-64
Practice
If 250 mL of solution contains 90 mg of drug, there
would be 450 mg of drug in how many mL of
solution?
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
mg
mg 450
x
90 =
mL
250
Answer = 1,250 mL

65. 3-65
In Summary
 In this chapter you learned to:
 convert values to and from a percent;
 convert values to and from a ratio.
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.

66. 3-66
In Summary (cont.)
 In this chapter you learned to:
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
 write proportions;
 use proportions to solve for an unknown
quantity.

67. 3-67
ANSWER: 145% ANSWER: 5.6%
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Apply Your Knowledge
Convert to percent:
1.45 0.056
Convert to a decimal:
15.6 % 0.89%
ANSWER: 0.156 ANSWER: 0.0089

68. 3-68
75 ANSWER: 75:125
4
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Apply Your Knowledge
Convert to a ratio:
125
Convert to a fraction:
78:10
5
ANSWER: 7

69. 3-69
Apply Your Knowledge
Determine if the following are true proportions:
45:90 = 15:30
ANSWER: True proportion
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
6/7 = 3/4
ANSWER: Not a true proportion

70. 3-70
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
Apply Your Knowledge
Solve for the unknown:
25mg:6mL=x:12mL
ANSWER: 50mg
22/x=12/18
ANSWER: 33

71. 3-71
© 2012 The McGraw-Hill Companies, Inc. All rights reserved.
End of Chapter 3
If what you're
working for
really matters,
you'll give it all
you've got.
~ Nido Qubein