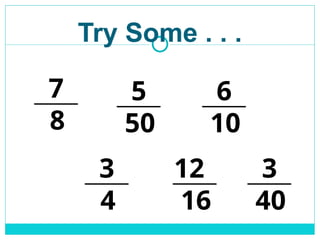
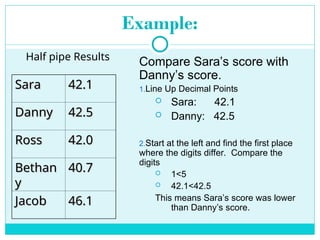
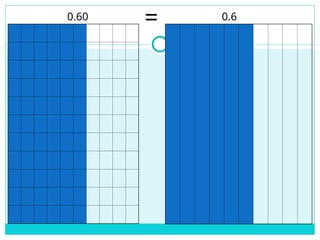
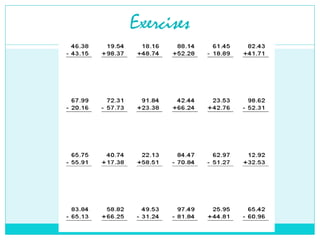
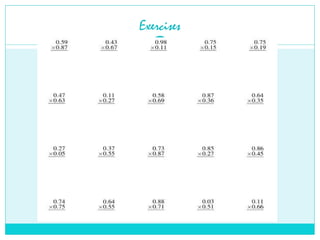
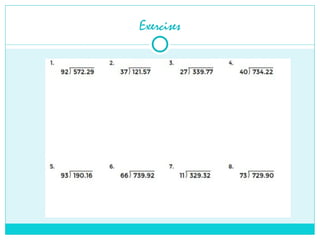
Decimals are a way of writing numbers that are not whole, using a decimal point (.) to separate the whole part from the fractional part.
🔹 What is a Decimal?
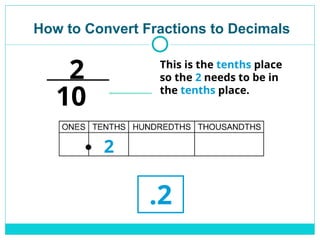
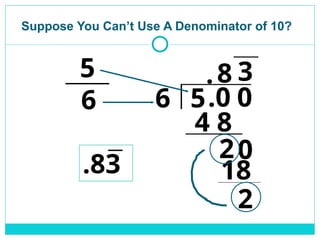
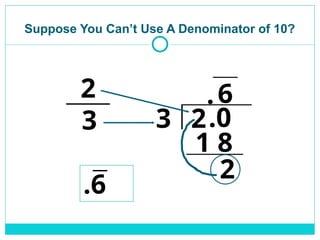
A decimal shows parts of a whole, based on powers of 10.
For example:
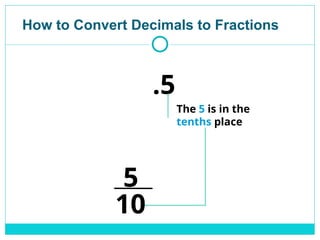
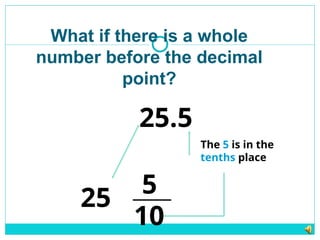
3.5 means 3 whole parts and 5 tenths.
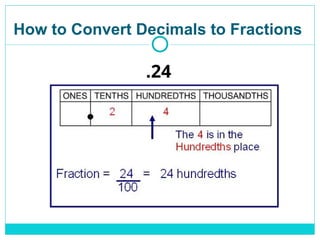
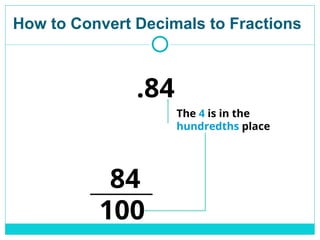
0.75 means 75 hundredths.
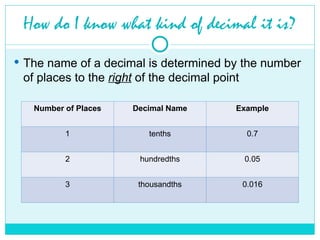
🔹 Place Values After the Decimal:
Each place after the decimal point has a special name:
0.1 → tenths
0.01 → hundredths
0.001 → thousandths
Decimals help us represent and work with numbers that aren't whole, using powers of 10. They're essential for precise calculations in daily life.