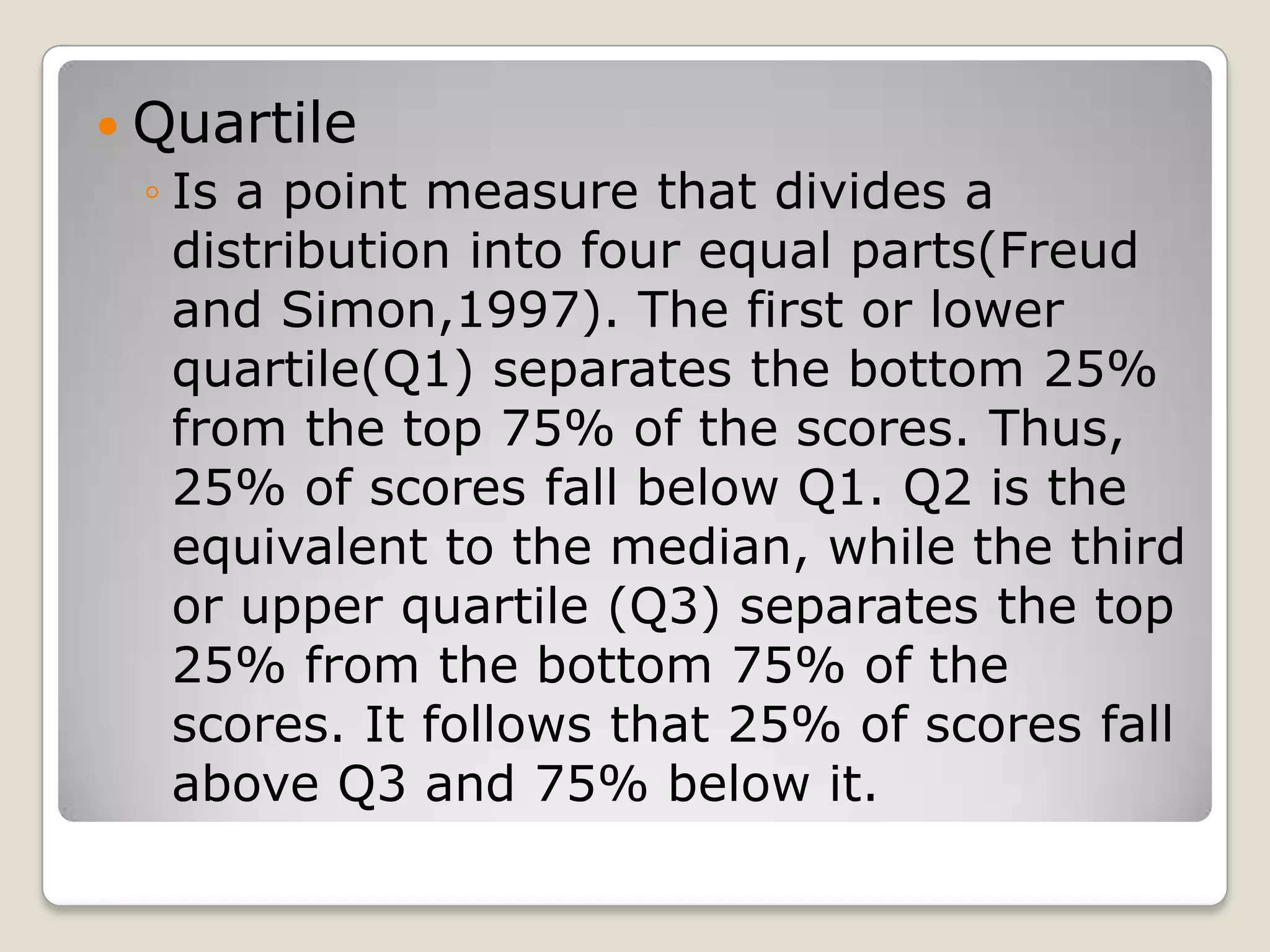
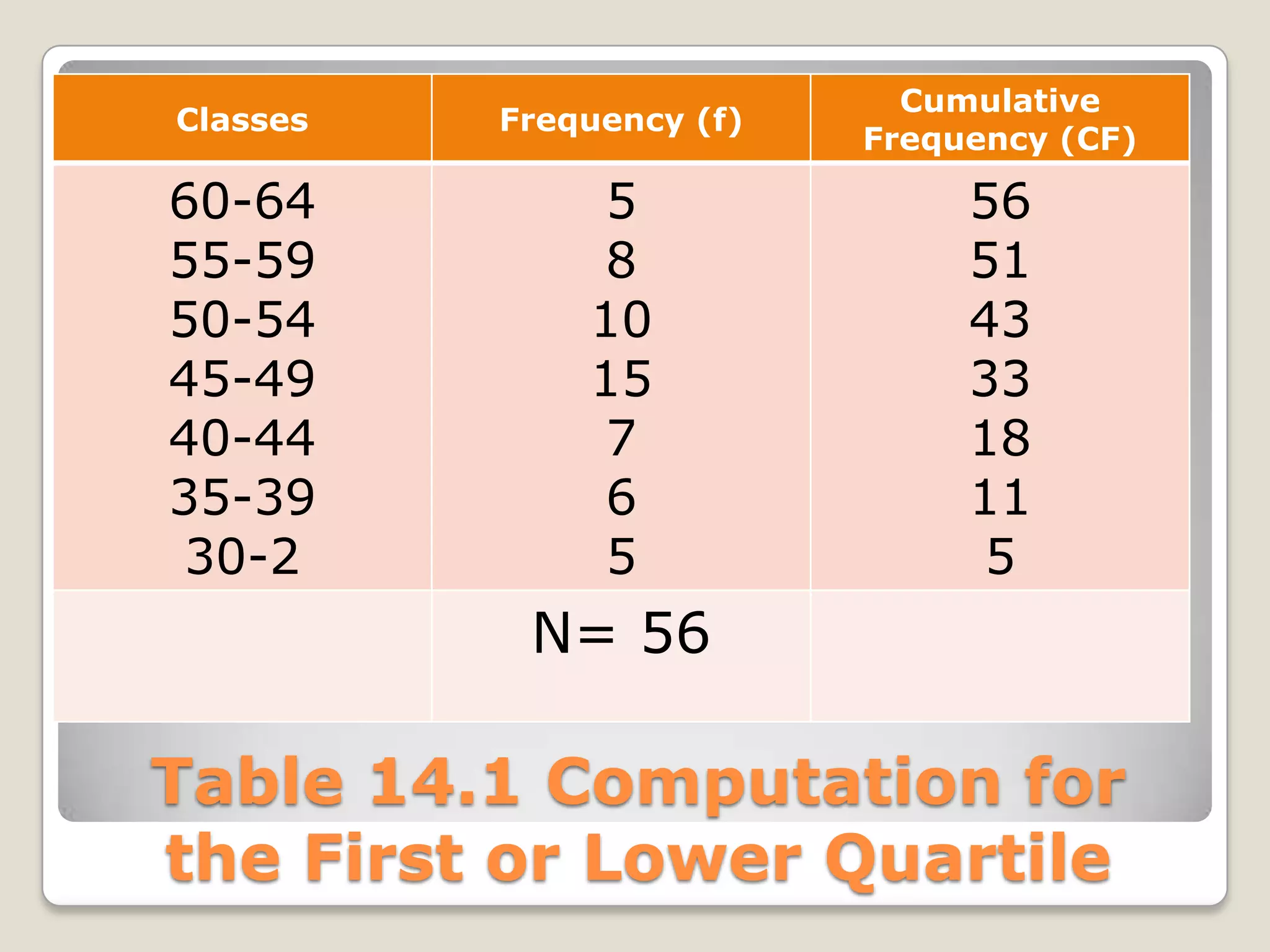
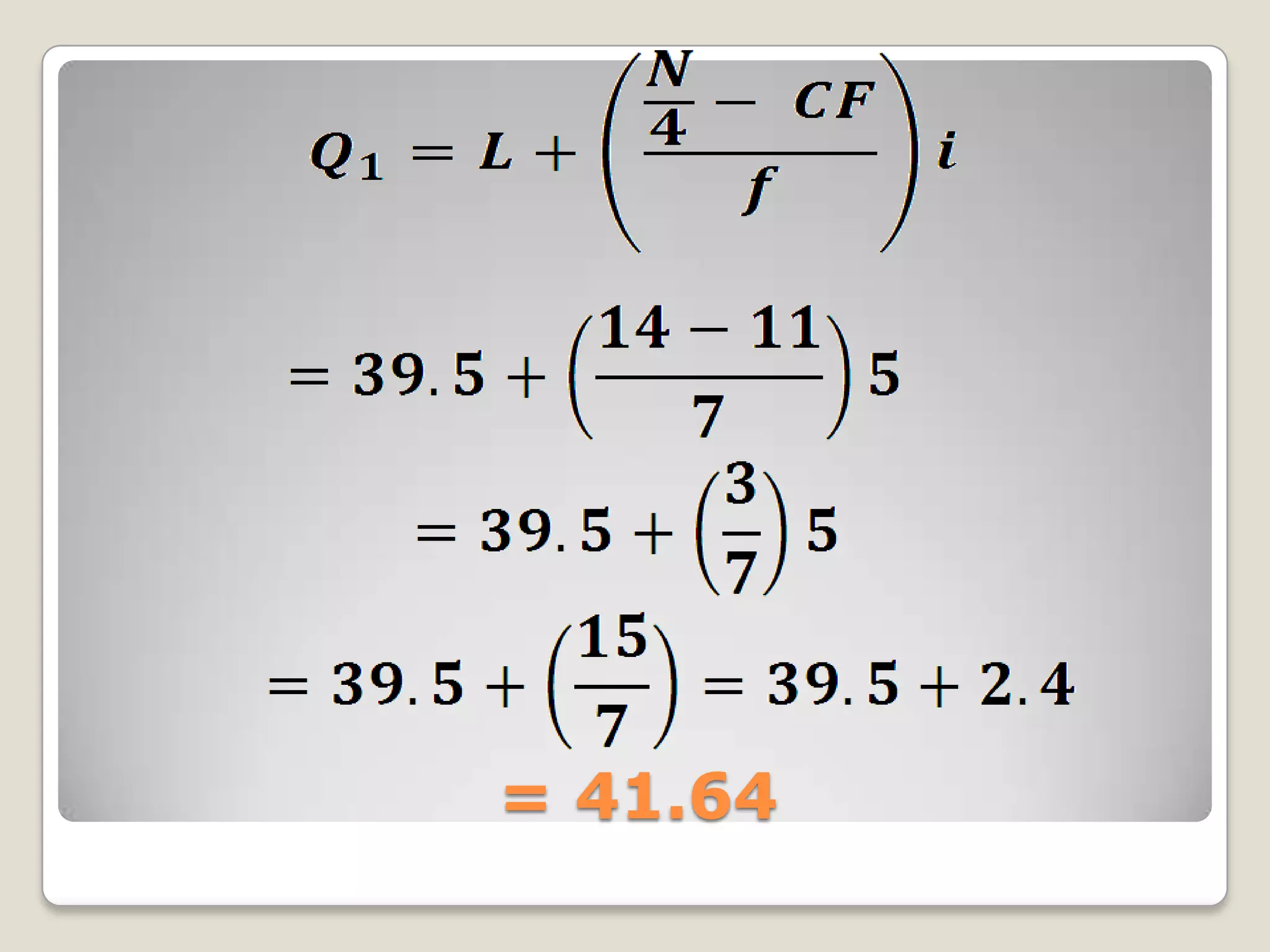This document discusses measures of relative standing that can be used to describe a student's test score in relation to other students, including quartiles, deciles, percentiles, percentile ranks, and z-scores. It focuses on explaining how to calculate the first (Q1) and third (Q3) quartiles. Q1 separates the lowest 25% of scores, while Q3 separates the highest 25%. The steps provided show how to determine the class boundaries and compute the exact quartile values using a grouped frequency distribution table.

1. CHAPTER 14
SUMMARIZING TEST
SCORES: MEASURES OF
RELATIVE STANDING

2. There vare occasions when
teachers are interested in
describing the relative
position of student’s score
in relation to scores
obtained by the whole
class.

3. Measures of relative
standing- are descriptive
measures that locate the
relative position of a test
score in relation to the
other scores obtained by a
group of students or test
takers.

4. The following measures of
relative standing that shall be
explored in this chapter are
the following
◦Quartile
◦Decile
◦Percentile
◦Percentile rank
◦Z score

5.  Quartile
◦ Is a point measure that divides a
distribution into four equal parts(Freud
and Simon,1997). The first or lower
quartile(Q1) separates the bottom 25%
from the top 75% of the scores. Thus,
25% of scores fall below Q1. Q2 is the
equivalent to the median, while the third
or upper quartile (Q3) separates the top
25% from the bottom 75% of the
scores. It follows that 25% of scores fall
above Q3 and 75% below it.

6.  In computing Q1 for grouped test scores,
the following steps have to be
observed(Weiss,1997).
◦ 1. Cumulate the frequencies from the lowest to
the highest class interval.
◦ 2. Determine one-fourth or 25% of the number
of test scores in the grouped frequency
distribution by dividing N by

7. ◦ 3. Look for the cumulative frequency that
approximates N/4. the class above it is Q1
class.
◦ 4. Get the exact lower limit and frequency of
the Q1 class.
◦ 5. Get the total number of scores (N) and the
class size.
◦ 6. Substitute all obtained values from step 2 to
step 5 into the follwing computational formula:

8. Where:
 L= exact lower limit of the Q1 class
 N/4 = locator of the Q1 class
 N= total number of scores
 CF= cumulative frequency before the Q1
class
 f= frequency of the Q1 class
 i= class size

9. Table 14.1 Computation for
the First or Lower Quartile
Classes Frequency (f)
Cumulative
Frequency (CF)
60-64
55-59
50-54
45-49
40-44
35-39
30-2
5
8
10
15
7
6
5
56
51
43
33
18
11
5
N= 56

10. CF= 11 f= 7
Q1 CLASS= 40-44
L= 39.5 i= 5
Q1 class= 40-44
L=39.5
CF= 11
i= 5
f= 7

11. = 41.64

12.  The procedures in computing the
third or upper quartile are as
follows:
◦ 1. cumulate the frequencies from the
lowest to the highest class interval.
◦ 2. determine three- fourths or 75% of
the number of test scores In the
grouped frequency that approximates
3N by
◦ 3. look for the cumulative frequency that
approximates .The class above it is
the Q3 class.

13.  4. get the exact lower limit and frequency
of the Q3 class.
 Get the total number of scores (N) and
the class size.
 Substitute all obtained values from step 2
to step 5 into the following computational
formula:

14.  Where:
 L= exact lower limit of the Q3 class
 3N/4= locator of the Q3 class
 N= total number of scores
 CF= cumulative frequency before the Q3
class
 f= frequency of the Q3 class
 i= class size