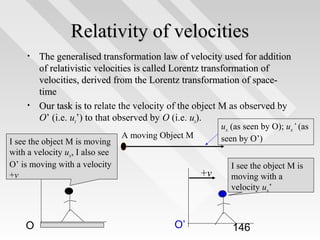
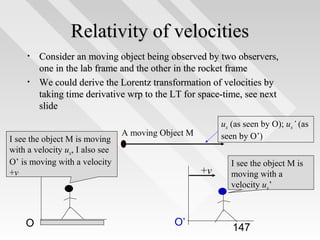
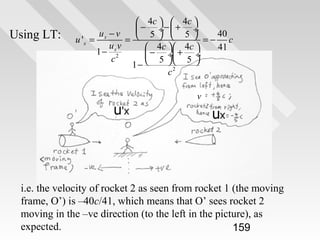
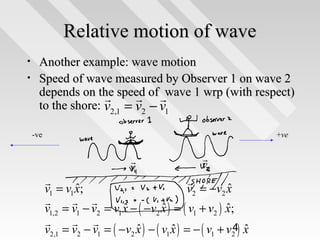
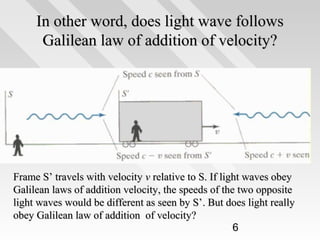
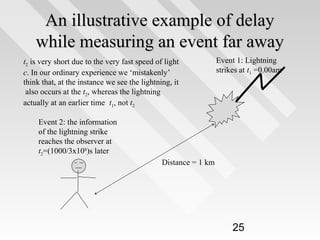
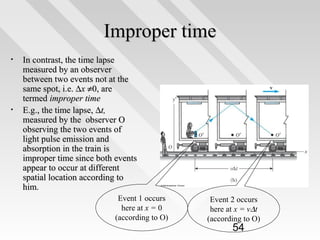
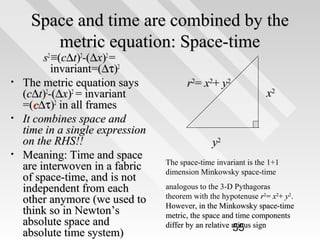
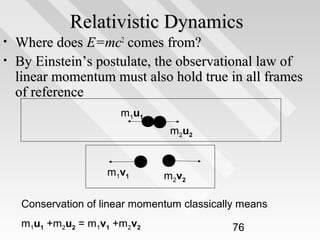
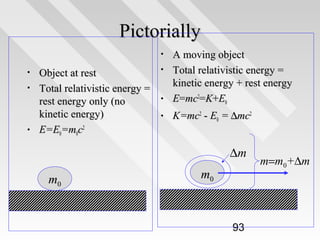
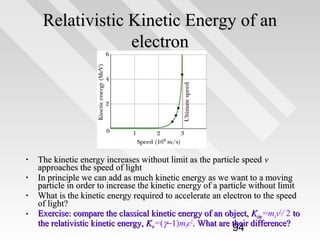
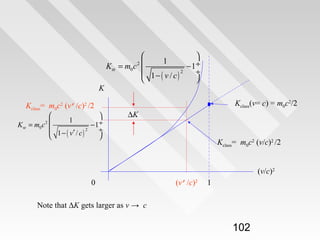
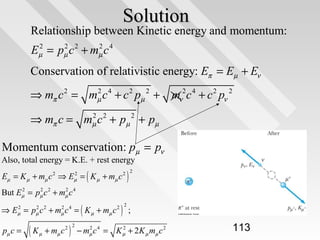
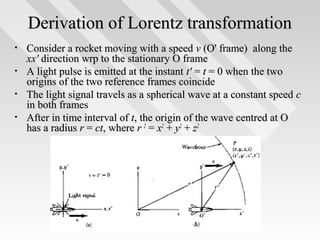
This document discusses key concepts from special relativity. It begins with an example of measuring the rate of dripping water from a pot on a moving train from the perspective of an observer on the train (Ali) and an observer on the ground (Baba). It notes that both measurements are equally valid and can be related using Lorentz transformations. It then discusses that events can be considered from any reference frame, with no frame being superior, and that the choice of reference frame is a matter of convenience. It also explains that accurately locating events requires accounting for the finite speed of light to avoid simultaneity issues. Overall, the document introduces the idea that the laws of physics must appear the same in all reference frames according to Einstein's principle

1. Special theory of Relativity
Notes based on
Understanding Physics
by Karen Cummings et al., John Wiley & Sons
1

2. An open-chapter question
•
•
Let say you have found a map revealing a huge galactic treasure
at the opposite edge of the Galaxy 200 ly away.
Is there any chance for you to travel such a distance from Earth
and arrive at the treasure site by traveling on a rocket within your
lifetime of say, 60 years, given the constraint that the rocket
cannot possibly travel faster than the light speed?
Treasure’s
here
You are here
2

3. Relative motions at ordinary speed
•
•
•
Relative motion in ordinary
life is commonplace
E.g. the relative motions of
two cars (material objects)
along a road
When you observe another
car from within your car, can
you tell whether you are at
rest or in motion if the other
car is seen to be “moving?”
3

4. Relative motion of wave
•
•
Another example: wave motion
Speed of wave measured by Observer 1 on wave 2
depends on the speed of rwave 1 wrp (with respect)
r
r
to the shore: v2,1 = v2 − v1
-ve
+ve
r
v1
r
v2
r
r
ˆ
ˆ
v1 = v1 x;
v2 = −v2 x
r
r r
ˆ
ˆ
ˆ
v1,2 = v1 − v2 = v1 x − ( −v2 x ) = ( v1 + v2 ) x;
r
r r
4 ˆ
ˆ
ˆ
v2,1 = v2 − v1 = ( −v2 x ) − ( v1 x ) = − ( v1 + v2 ) x

5. Query: can we surf light waves?
•
•
•
Light is known to be wave
If either or both wave 1 and wave 2 in the
previous picture are light wave, do they
follow the addition of velocity rule too?
Can you surf light wave ? (if so light shall
appear at rest to you then)
5

6. In other word, does light wave follows
Galilean law of addition of velocity?
Frame S’ travels with velocity v relative to S. If light waves obey
Galilean laws of addition velocity, the speeds of the two opposite
light waves would be different as seen by S’. But does light really
obey Galilean law of addition of velocity?
6

7. The negative result of MichelsonMorley experiment on Ether
•
•
•
•
•
In the pre-relativity era, light is thought to be propagating in a medium called
ether an direct analogy to mechanical wave propagating in elastic medium such as
sound wave in air
If exist, ether could render measurable effect in the apparent speed of light in
various direction
However Michelson-Morley experiment only find negative result on such
effect
A great puzzlement to the contemporary physicist: what does light wave
move relative to?
7

8. How could we know whether we are
at rest or moving?
•
•
Can we cover the
windows of our car
and carry out
experiments inside to
tell whether we are at
rest or in motion?
NO
8

9. In a “covered” reference frame, we
can’t tell whether we are moving or
at rest
•
Without referring to an external reference
object (such as a STOP sign or a lamp
post), whatever experiments we conduct in
a constantly moving frame of reference
(such as a car at rest or a car at constant
speed) could not tell us the state of our
motion (whether the reference frame is at
rest or is moving at constant velocity)
9

10. 《尚書經．考靈曜》
•
•
「地恒動不止，而人不知，譬如人在大
舟中，閉牖而坐，舟行而不覺也。」
“The Earth is at constant state of motion yet
men are unaware of it, as in a simile: if one
sits in a boat with its windows closed, he
would not aware if the boat is moving” in
“Shangshu jing”, 200 B.C
10

11. Physical laws must be invariant in
any reference frame
•
•
•
•
Such an inability to deduce the state of motion is a
consequence of a more general principle:
There must be no any difference in the physical
laws in any reference frame with constant velocity
(which would otherwise enable one to differentiate
the state of motion from experiment conducted in
these reference frame)
Note that a reference frame at rest is a special case
of reference frame moving at constant velocity
(v = 0 = constant)
11

12. The Principle of Relativity
•
All the laws of Physics are the same in
every reference frame
12

13. Einstein’s Puzzler about running fast
while holding a mirror
•
•
•
•
Says Principle of Relativity: Each fundamental constants must
have the same numerical value when measured in any reference
frame (c, h, e, me, etc)
(Otherwise the laws of physics would predict inconsistent
experimental results in different frame of reference – which must
not be according to the Principle)
Light always moves past you with the same speed c, no matter
how fast you run
Hence: you will not observe light waves to slow down as you
move faster
13

14. c, one of the fundamental constants
of Nature
14

15. Constancy of the speed of light
15

16. Reading Exercise (RE) 38-2
•
•
•
•
While standing beside a railroad track, we are startled by a boxcar traveling
past us at half the speed of light. A passenger (shown in the figure) standing at
the front of the boxcar fires a laser pulse toward the rear of the boxcar. The
pulse is absorbed at the back of the box car. While standing beside the track we
measure the speed of the pulse through the open side door.
(a) Is our measured value of the speed of the pulse greater than, equal to, or less
than its speed measured by the rider?
(b) Is our measurement of the distance between emission and absorption of the
light pulse great than, equal to, or less than the distance between emission and
absorption measured by the rider?
(c) What conclusion can you draw about the relation between the times of flight
of the light pulse as measured in the two reference frames?
16

17. Touchstone Example 38-1:
Communication storm!
•
A sunspot emits a tremendous burst of particles that travels
toward the Earth. An astronomer on the Earth sees the
emission through a solar telescope and issues a warning.
The astronomer knows that when the particle pulse arrives
it will wreak havoc with broadcast radio transmission.
Communications systems require ten minutes to switch
from over-the-air broadcast to underground cable
transmission. What is the maximum speed of the particle
pulse emitted by the Sun such that the switch can occur in
time, between warning and arrival of the pulse? Take the
sun to be 500 light-seconds distant from the Earth.
17

18. Solution
It takes 500 seconds for the warning light flash to travel the distance of 500
light-seconds between the Sun and the Earth and enter the astronomer’s
telescope. If the particle pulse moves at half the speed of light, it will take
twice as long as light to reach the Earth. If the pulse moves at one-quarter the
speed of light, it will take four times as long to make the trip. We generalize
this by saying that if the pulse moves with speed v/c, it will take time to make
the trip given by the expression:
∆tpulse = 500 s/ (vpulse/c)
•
How long a warning time does the Earth astronomer have between arrival of
the light flash carrying information about the pulse the arrival of the pulse
itself? It takes 500 seconds for the light to arrive. Therefore the warning time
is the difference between pulse transit time and the transit time of light:
∆twarning = ∆tpulse - 500 s.
•
But we know that the minimum possible warning time is 10 min = 600 s.
•
Therefore we have
•
600 s = 500 s / (vpulse/c) – 500 s,
•
which gives the maximum value for vpuls if there is to he sufficient time for
warning:
vpuls = 0.455 c.
(Answer)
•
Observation reveals that pulses of particles emitted from the sun travel much
18
slower than this maximum value. So we would have much longer warning
time than calculated here.
•

19. Relating Events is science
•
•
•
Science: trying to relate one event to another event
E.g. how the radiation is related to occurrence of
cancer; how lightning is related to electrical
activities in the atmosphere etc.
Since observation of events can be made from
different frames of reference (e.g. from an
stationary observatory or from a constantly
moving train), we must also need to know how to
predict events observed in one reference frame
will look to an observer in another frame
19

20. Some examples
•
•
How is the time interval measured between
two events observed in one frame related to
the time interval measured in another frame
for the same two events?
How is the velocity of a moving object
measured by a stationary observer and that
by a moving observer related?
20

21. Defining events
•
So, before one can work out the relations
between two events, one must first precisely
define what an event is
21

22. Locating Events
•
•
•
•
An event is an occurrence that happens at a
unique place and time
Example: a collision, and explosion, emission of a
light flash
An event must be sufficiently localised in space
and time
e.g. your birthday: you are born in the General
Hospital PP at year 1986 1st April 12.00 am)
22

23. Example of two real-life events
Event 1: She said “I love you”
July 1Dec, 12.01:12 am, Tasik Aman
Event 2: She said “Let’s break up-lah”
27 Dec 2005, 7.43:33 pm, Tasik Harapan
23

24. Subtle effect to locate an event:
delay due to finiteness of light speed
•
•
In our (erroneous) “common sense”
information are assumed to reach us
instantaneously as though it is an immediate
action through a distance without any delay
In fact, since light takes finite time to travel,
locating events is not always as simple it
might seems at first
24

25. An illustrative example of delay
while measuring an event far away
t2 is very short due to the very fast speed of light
c. In our ordinary experience we ‘mistakenly’
think that, at the instance we see the lightning, it
also occurs at the t2, whereas the lightning
actually at an earlier time t1, not t2
Event 1: Lightning
strikes at t1 =0.00am
Event 2: the information
of the lightning strike
reaches the observer at
t2=(1000/3x108)s later
Distance = 1 km
25

26. Reading Exercise 38-4
•
•
•
When the pulse of protons passes through detector
A (next to us), we start our clock from the time t =
0 microseconds. The light flash from detector B
(at distance L=30 m away) arrives back at detector
A at a time t = 0.225 microsecond later.
(a) At what time did the pulse arrive at detector B?
(b) Use the result from part (a) to find the speed at
which the proton pulse moved, as a fraction of the
speed of light.
26

27. Answer
•
•
•
The time taken for light pulse to travel from B to
A is L/c = 10-7 s =0.1 µs
Therefore the proton pulse arrived detector B
0.225 – 0.1 µs = 0.125 µs after it passed us at
detector A.
(b) The protons left detector A at t =0 and,
according to part (a), arrived at detector B at t =
0.125 µs. Therefore its speed from A to B is
L/0.125 µs = …=0.8c
27

28. Redefining Simultaneity
•
•
•
•
Hence to locate an event accurately we must take
into account the factor of such time delay
An intelligent observer is an observer who, in an
attempt to register the time and spatial location of
an event far away, takes into account the effect of
the delay factor
(In our ordinary daily life we are more of an
unintelligent observer)
For an intelligent observer, he have to redefine the
notion of “simultaneity” (example 38-2)
28

29. Example 38-2:
Simultaneity of the Two Towers
•
Frodo is an intelligent observer
standing next to Tower A,
which emits a flash of light
every l0 s. 100 km distant from
him is the tower B, stationary
with respect to him, that also
emits a light flash every 10 s.
Frodo wants to know whether
or not each flash is emitted
from remote tower B
simultaneous with (at the same
time as) the flash from Frodo’s
own Tower A. Explain how to
do this with out leaving Frodo
position next to Tower A. Be
specific and use numerical
values.
29

30. Solution
•
•
•
•
•
Frodo is an intelligent observer, which means that he know
how to take into account the speed of light in determining
the time of a remote event, in this case the time of emission
of a flash by the distant Tower B. He measures the time
lapse between emission of a flash by his Tower A and his
reception of flash from Tower B.
If this time lapse is just that required for light move from
Tower B to Tower A, then the two emissions occur the
same time.
The two Towers are 100 km apart. Call this distance L.
Then the time t for a light flash to move from B to A is
t = L/c = l05 m/3 × 108 m/s = 0.333 ms. (ANS)
If this is the time Frodo records between the flash nearby
Tower A and reception of the flash from distant tower then
he is justified in saying that the two Towers emit flashes
simultaneously in his frame.
30

31. One same event can be considered in
any frame of reference
•
•
•
One same event, in principle, can be measured by
many separate observers in different (inertial) frames
of reference (reference frames that are moving at a
constant velocity with respect to each other)
Example: On the table of a moving train, a cracked
pot is dripping water
The rate of the dripping water can be measured by
(1) Ali, who is also in the train, or by (2) Baba who
is an observer standing on the ground. Furthermore,
you too can imagine (3) ET is also performing the
same measurement on the dripping water from
Planet Mars. (4) By Darth Veda from Dead Star…
31

32. No ‘superior’ (or preferred) frame
•
•
•
In other words, any event can be considered
in infinitely many different frames of
references.
No particular reference frame is ‘superior’
than any other
In the previous example, Ali’s frame is in no
way superior than Baba’s frame, nor ET’s
frame, despite the fact that the water pot is
stationary with respect to Ali.
32

33. Transformation laws
•
•
•
•
Measurements done by any observers from all frame
of reference are equally valid, and are all equivalent.
Transformation laws such as Lorentz transformation
can be used to relate the measurements done in one
frame to another.
In other words, once you know the values of a
measurement in one frame, you can calculate the
equivalent values as would be measured in other
frames.
In practice, the choice of frame to analyse any event
is a matter of convenience.
33

34. Example 1
•
•
•
•
•
•
•
In the previous example, obviously, the pot is stationary with
respect to Ali, but is moving with respect to Baba.
Ali, who is in the frame of the moving train, measures that the
water is dripping at a rate of, say, rA.
Baba, who is on the ground, also measures the rate of dripping
water, say rB.
Both of the rates measured by Ali and that measured by Baba
have equal status – you can’t say any one of the measurements is
‘superior’ than the other
One can use Lorentz transformation to relate rA with rB. In reality,
we would find that rB = rA /γ where
1/γ2 = 1 − (v/c)2, with v the speed of the train with respect to
ground, and c the speed of light in vacuum.
Note: rB is not equal to rA (would this contradict your
expectation?)
34

35. Against conventional wisdom?
•
•
•
•
According to SR, rA and rB are different in general.
This should come as a surprise as your
conventional wisdom (as according to Newtonian
view point) may tell you that both rA and rB should
be equal in their numerical value.
However, as you will see later, such an assumption
is false in the light of SR since the rate of time flow
in two frames in relative motion are different
Both rates, rA and rB, despite being different, are
correct in their own right.
35

36. Example 2
•
•
•
Consider a stone is thrown into the air making a projectile
motion.
If the trajectory of the stone is considered in the frame of
Earth (the so-called Lab frame, in which the ground is
made as a stationary reference), the trajectory of the stone
is a parabolic curve.
The trajectory of the stone can also be analysed in a
moving frame traveling at velocity vx along the same
horizontal direction as the stone. In this frame (the socalled rocket frame), the trajectory of the stone is not a
parabolic curve but a vertical line.
36

37. View from different frames
•
In the Lab frame, the
observer on the
ground sees a
parabolic trajectory
•
In the Rocket frame,
the pilot sees the
projectile to follow a
vertically straight line
downwards
37

38. •
•
•
Transformation law for the
coordinates • In rocket frame
In Lab frame
y = – (gt2)/2 + H
x = vxt
•
•
•
•
y’ = – (gt2)/2
x’ = 0
Transformation law relating the coordinates
of projectile in both frames is
y’ = y - H ,
x’ = x - vxt
y’ = 0
y
H
y’
y=0
38

39. Time dilation as direct consequence
of constancy of light speed
•
•
•
•
•
According to the Principle of Relativity, the speed
of light is invariant (i.e. it has the same value) in
every reference frame (constancy of light speed)
A direct consequence of the constancy of the speed
of light is time stretching
Also called time dilation
Time between two events can have different values
as measured in lab frame and rocket frames in
relative motion
“Moving clock runs slow”
39

40. Experimental verification of
time stretching with pions
•
•
•
•
•
•
•
•
•
Pion’s half life t½ is 18 ns.
Meaning: If N0 of them is at rest in the beginning, after 18 ns,
N0 /2 will decay
Hence, by measuring the number of pion as a function of time
allows us to deduce its half life
Consider now N0 of them travel at roughly the speed of light c, the
distance these pions travel after t½=18 ns would be ct½ ≈5.4 m.
Hence, if we measure the number of these pions at a distance 5.4
m away, we expect that N0 /2 of them will survive
However, experimentally, the number survived at 5.4m is much
greater than expected
The flying poins travel tens of meters before half of them decay
How do you explain this? the half life of these pions seems to
have been stretched to a larger value!
Conclusion: in our lab frame the time for half of the pions to
decay is much greater than it is in the rest frame of the pions!
40

41. RE 38-5
•
•
Suppose that a beam of pions moves so fast that at
25 meters from the target in the laboratory frame
exactly half of the original number remain
undecayed. As an experimenter, you want to put
more distance between the target and your
detectors. You are satisfied to have one-eighth of
the initial number of pions remaining when they
reach your detectors. How far can you place your
detectors from the target?
ANS: 75 m
41

42. •
•
•
•
A Gedanken Experiment
Since light speed c is invariant (i.e. the same in all frames), it is
Since light speed c is invariant (i.e. the same in all frames), it is
suitable to be used as a clock to measure time and space
Use light and mirror as clock – light clock
A mirror is fixed to a moving vehicle, and a light pulse leaves O’
at rest in the vehicle. O’ is the rocket frame.
Relative to a lab frame observer on Earth, the mirror and O’ move
with a speed v.
42

43. In the rocket frame
•
•
•
The light pulse is
observed to be moving in
the vertical direction only
The distance the light
pulse traversed is 2d
The total time travel by
the light pulse to the top,
get reflected and then
return to the source is ∆τ
= 2d/c
43

44. In the lab frame
•
•
•
However, O in the lab frame
observes a different path
taken by the light pulse – it’s
a triangle instead of a
vertical straight line
The total light path is longer
= 2l
l2=(c∆t/2)2
=d2 + (∆x/2)2
=d2 + (v∆t/2)2
∆x=(v∆t)
l
l
∆x/2=
44

45. Light triangle
•
•


We can calculate the
relationship between ∆t, ∆τ
and v:
l2=(c∆t/2)2=d2 +(v∆t/2)2
(lab frame)
∆τ = 2d/c (Rocket frame)
Eliminating d,
∆t =
∆τ
2
v
1−  ÷
c
= γ∆τ
γ=
l
l
∆x/2=
1
2
v
1−  ÷
c
≥1
45

46. Time dilation equation
∆τ
∆t =
= γ∆τ
•
Time dilation equation
•
Gives the value of time ∆τ between two events
occur at time ∆t apart in some reference frame
γ=
1
2
v
1−  ÷
c
≥1
•
Lorentz factor
•
Note that as v << c, γ ≈ 1; as v  c, γ ∞
Appears frequently in SR as a measure of
relativistic effect: γ ≈ 1 means little SR effect; γ >>
1 is the ultra-relativistic regime where SR is most
pronounce
•
2
v
1−  ÷
c
46

47. RE 38-6
•
A set of clocks is assembled in a stationary boxcar. They
include a quartz wristwatch, a balance wheel alarm clock,
a pendulum grandfather clock, a cesium atomic clock, fruit
flies with average individual lifetimes of 2.3 days. A clock
based on radioactive decay of nuclei, and a clock timed by
marbles rolling down a track. The clocks are adjusted to
run at the same rate as one another. The boxcar is then
gently accelerated along a smooth horizontal track to a
final velocity of 300 km/hr. At this constant final speed,
which clocks will run at a different rate from the others as
measured in that moving boxcar?
47

48. The Metric Equation
•
•
•
From the light triangle in
lab frame and the vertical
light pulse in the rocket
frame:
l2= (c∆t/2)2=d2 + (∆x/2)2;
l
l
∆x/2=
d = c∆τ/2
⇒(c∆t/2)2=(c∆τ/2)2+(∆x/2)2
•
Putting the terms that refer to
the lab frame are on the right: (c∆τ)2=(c∆t)2-(∆x)2
48

49. •
•
•
•
•
•
•
“the invariant space-time
interval”
We call the RHS, s2 ≡ (c∆t)2-(∆x)2 “invariant space-time interval
squared” (or sometimes simply “the space-time interval”)
In words, the space-time interval reads:
s2 = (c×time interval between two events as observed in the frame)2 (distance interval between the two events as observed in the frame) 2
We can always calculate the space-time intervals for any pairs of
events
The interval squared s2 is said to be an invariant because it has the
same value as calculated by all observers (take the simile of the
mass-to-high2 ratio)
Obviously, in the light-clock gadanken experiment, the space-time
interval of the two light pulse events s2 ≡ (c∆t)2-(∆x)2 = (c∆τ)2 is
positive because (c∆τ)2 > 0
The space-time interval for such two events being positive is deeply
related to the fact that such pair of events are causally related
49

50. Time-like, space-like and light-like
•
•
•
•
The space-time interval of event pairs is said to be
“time-like” (because the time component in the
interval is larger in magnitude than the spatial
component) if s2>0.
Not all pairs of events has a positive space-time
interval.
Pairs of events with a negative value of space-time
interval is said to be “space-like”, and these pairs
of event cannot be related via any causal relation
Pairs of events with s2 = 0 is said to be “light like”.
50

51. RE 38-8
•
•
•
•
•
Points on the surfaces of the Earth and the Moon that face
each other are separated by a distance of 3.76 × 108 m.
(a) How long does it take light to travel between these
points?
A firecraker explodes at each of these two points; the time
between these explosion is one second.
(b) What is the invariant space-time interval for these two
events?
Is it possible that one of these explosions caused the other
explosion?
51

52. Solution
(a)
(b)
(c)
Time taken is
t = L / c = 3.76×108 m/ 3× 108 m/s = 1.25 s
s2= (ct)2 - L2
= (3×108 m/s × 1.25 s)2 –(3.76×108 m)2 = - 7.51 m2
(space-like interval)
It is known that the two events are separated by only 1 s.
Since it takes 1.25 s for light to travel between these point, it
is impossible that one explosion is caused by the other, given
that no information can travel fast than the speed of light.
Alternatively, from (b), these events are separated by a spacelike space-time interval. Hence it is impossible that the two
explosions have any causal relation
52

53. Proper time
•
•
•
Imagine you are in the rocket frame, O’, observing
two events taking place at the same spot, separated
by a time interval ∆τ (such as the emission of the
light pulse from source (EV1), and re-absorption
of it by the source again, (EV2))
Since both events are measured on the same spot,
they appeared at rest wrp to you
The time lapse ∆τ between the events measured on
the clock at rest is called the proper time or
wristwatch time (one’s own time)
53

54. Improper time
•
•
In contrast, the time lapse
measured by an observer
between two events not at the
same spot, i.e. ∆x ≠0, are
termed improper time
E.g., the time lapse, ∆t,
measured by the observer O
observing the two events of
light pulse emission and
absorption in the train is
improper time since both events
appear to occur at different
spatial location according to
him.
Event 1 occurs
here at x = 0
(according to O)
Event 2 occurs
here at x = v∆t
(according to O)
54

55. Space and time are combined by the
metric equation: Space-time
•
•
•
s2 ≡(c∆t)2-(∆x)2 =
invariant=(∆τ)2
The metric equation says
(c∆t)2-(∆x)2 = invariant
=(c∆τ)2 in all frames
It combines space and
time in a single expression
on the RHS!!
Meaning: Time and space
are interwoven in a fabric
of space-time, and is not
independent from each
other anymore (we used to
think so in Newton’s
absolute space and
absolute time system)
r2= x2+ y2
x2
y2
The space-time invariant is the 1+1
dimension Minkowsky space-time
analogous to the 3-D Pythagoras
theorem with the hypotenuse r2= x2+ y2.
However, in the Minkowsky space-time
metric, the space and time components
differ by an relative minus sign
55

56. s relates two different measures
of time between the same two
events
2
s2 ≡(c∆t)2-(∆x)2 = invariant=(c∆τ)2
•
•
•
(1) the time recorded on clocks in the reference frame in
which the events occur at different places (improper time,
∆t), and
(2) the wristwatch time read on the clock carried by a
traveler who records the two events as occurring a the
same place (proper time, ∆τ)
In different frames, ∆t and ∆x measured for the same two
events will yield different values in general. However, the
interval squared, (c∆t)2-(∆x)2 will always give the same
value, see example that ensues
56

57. Example of calculation of spacetime interval squared
•
•
•
•
•
In the light-clock gedanken experiment: For
O’, he observes the proper time interval of the
two light pulse events to be ∆τ. For him, ∆x’ =
0 since these events occur at the same place
Hence, for O’,
s’ 2 = (c×time interval observed in the frame)2 (distance interval observed in the frame)2
= (c∆τ)2 - (∆x’ )2 = (c∆τ )2
For O, the time-like interval for the two events
is s2=(c∆t)2-(∆x)2 = (cγ∆τ)2-(v∆t)2 = (cγ∆τ)257
(vγ∆τ)2 = γ2 (c2-v2)∆τ2 = c2∆τ2 =s’ 2

58. What happens at high and low speed
∆t = γ∆τ ,
•
•
•
•
γ=
1
2
v
1−  ÷
c
≥1
At low speed, v << c, γ ≈ 1, and ∆τ ≈∆t, not much different, and we
can’t feel their difference in practice
However, at high speed, proper time interval ( ∆τ) becomes much
SMALLER than improper time interval (∆t) in comparison, i.e.
∆τ = ∆t/γ << ∆t
Imagine this: to an observer on the Earth frame, the person in a rocket
frame traveling near the light speed appears to be in a ‘slow motion’
mode. This is because, according to the Earth observer, the rate of
time flow in the rocket frame appear to be slower as compared to the
Earth’s frame rate of time flow.
A journey that takes, say, 10 years to complete, according to a traveler
on board (this is his proper time), looks like as if they take 10 γ yr
according to Earth observers.
58

59. Space travel with time-dilation
A spaceship traveling at speed v = 0.995c is sent to planet
100 light-year away from Earth
• How long will it takes, according to a Earth’s observer?
• ∆t = 100 ly/0.995c = 100.05yr
• But, due to time-dilation effect, according to the traveler on
board, the time taken is only
∆τ = ∆t/γ = ∆t√(1-0.9952) = 9.992 yr, not 100.05 yr as the
Earthlings think
• So it is still possible to travel a very far distance within
one’s lifetime (∆τ ≈ 50 yr) as long as γ (or equivalently, v)
is large enough
•
59

60. Nature’s Speed Limit
•
•
•
•
•
•
•
Imagine one in the lab measures the speed of a rocket v to
be larger than c.
2
v
As a consequence, according to ∆τ = ∆t 1 −  
 ÷
c
The proper time interval measurement ∆τ in the rocket
frame would be proportional to an imaginary number, i
=√(-1)
This is unphysical (and impossible) as no real time can be
proportional to an imaginary number
Conclusion: no object can be accelerated to a speed greater
than the speed of light in vacuum, c
Or more generally, no information can propagate faster
than the light speed in vacuum, c
Such limit is the consequence required by the logical
consistency of SR
60

61. Time dilation in ancient legend
•
•
天上方一日，人间已十年
One day in the heaven, ten years in the
human plane
61

62. RE 38-7
•
•
•
Find the rocket speed v at which the time ∆τ
between ticks on the rocket is recorded by
the lab clock as ∆t = 1.01∆τ
Ans: γ = 1.01, i.e. (v/c)2 =1 – 1/γ 2 = …
Solve for v in terms of c: v = …
62

63. Satellite Clock Runs Slow?
•
•
An Earth satellite in circular orbit just above the
atmosphere circles the Earth once every T = 90 min. Take
the radius of this orbit to be r = 6500 kilometers from the
center of the Earth. How long a time will elapse before the
reading on the satellite clock and the reading on a clock on
the Earth’s surface differ by one microsecond?
For purposes of this approximate analysis, assume that the
Earth does not rotate and ignore gravitational effects due
the difference in altitude between the two clocks
(gravitational effects described by general relativity).
63

64. dfds
Solution
•
•
•
•
•
•
•
•
•
•
First we need to know the speed of the satellite in orbit. From the radius of
the orbit we compute the circumference and divide by the time needed to
cover that circumference:
v = 2πr/T = (2π×6500 km)/(90 ×60 s) = 7.56 km/s
Light speed is almost exactly c = 3 × 105 km/s. so the satellite moves at the
fraction of the speed of light given by
(v /c)2 = [(7.56 km/s)/(3×105 km/s)]2 = (2.52 ×105)2 = 6.35×10-10.
The relation between the time lapse ∆τ recorded on the satellite clock and
the time lapse ∆t on the clock on Earth (ignoring the Earth’s rotation and
gravitational effects) is given by
∆τ = (1−(v /c)2)1/2 ∆t
We want to know the difference between ∆t and ∆τ i.e. ∆t - ∆τ:
We are asked to find the elapsed time for which the satellite clock and the
Earth clock differ in their reading by one microsecond, i.e. ∆t – ∆τ =1µs
Rearrange the above equation to read ∆t2 – ∆τ 2 = (∆t+∆τ)(∆t-∆τ), one shall
arrive at the relation that ∆t = [1+(1−(v/c)2)1/2](1µs) / (v/c)2 ≈ 3140s
This is approximately one hour. A difference of one microsecond between
atomic clock is easily detectable.
64

65. 65

66. Disagreement on simultaneity
Two events that are simultaneous in one
frame are not necessarily simultaneous in a
second frame in uniform relative motion
66

67. Example
No, I don’t agree. These two lightning
does not strike simultaneously
The two lightning strikes
simultaneously
67

68. Einstein Train illustration
•
Lightning strikes the
front and back of a
moving train, leaving
char marks on both
track and train. Each
emitted flash spreads
out in all directions.
I am equidistant from the front and back char
marks on the train. Light has the standard
speed in my frame, and equal speed in both
direction. The flash from the front of the train
arrived first, therefore the flash must have
left the front of the train first. The front
lightning bolt fell first before the rear light
bolt fell. I conclude that the two strokes are
not simultaneous.
I stand by the tracks halfway between the
char marks on the track. The flashes from
the strokes reach me a the same time and I
am equidistance from the char marks on the
track. I conclude that two events were
simultaneous
68

69. Why?
•
This is due to the invariance of the
space-time invariant in all frames, (i.e.
the invariant must have the same value
for all frames)
69

70. How invariance of space-time
interval explains disagreement on
simultaneity by two observers
•
•
•
•
•
Consider a pair of events with space-time interval
s2=(c∆t)2-(∆x)2 =(c∆t’ )2-(∆x’ )2
where the primed and un-primed notation refer to space
and time coordinates of two frames at relative motion (lets
call them O and O’ )
Say O observes two simultaneous event in his frame (i.e.
∆t = 0) and are separate by a distance of (∆x), hence the
space-time interval is s2 = - (∆x)2
The space-time interval for the same two events observed
in another frame, O’, s’ 2 = (c∆t’ )2- (∆x’ )2 must read the
same, as - (∆x)2
Hence, (c∆t’ )2 = (∆x’ )2 - (∆x)2 which may not be zero on
the RHS. i.e. ∆t’ is generally not zero. This means in
frame O’, these events are not observed to be occurring
simultaneously
70

71. Simulation of disagreement on simultaneity by two observers
(be aware that this simulation simulates the scenario in which
the lady in the moving car sees simultaneity whereas the
observer on the ground disagrees)
71

72. RE 38-9
•
•
•
Susan, the rider on the train pictured
in the figure is carrying an audio tape
player. When she received the light
flash from the front of the train she
switches on the tape player, which
plays very loud music. When she
receives the light flash from the back
end of the train, Susan switches off
the tape player. Will Sam, the
observers on the ground be able to
hear the music?
Later Susan and Sam meet for coffee
and examine the tape player. Will they
agree that some tape has been wound
from one spool to the other?
The answer is: …
72

73. Solution
•
•
Music has been emitted from the tape
player. This is a fact that must be true in
both frames of reference. Hence Sam on the
ground will be able to hear the music (albeit
with some distortion).
When the meet for coffee, they will both
agree that some tape has been wound from
one spool to the other in the tape recorder.
73

74. •
•
•
•
•
•
•
•
•
•
•
•
Touchstone Example 38-5: Principle
of Relativity Applied
Divide the following items into two lists, On one list, labeled SAME, place
Divide the following items into two lists, On one list, labeled SAME, place
items that name properties and laws that are always the same in every frame.
On the second list, labeled MAY BE DIF FERENT. place items that name
properties that can be different in different frames:
a. the time between two given events
b. the distance between two given events
c. the numerical value of Planck’s constant h
d. the numerical value of the speed of light c
e. the numerical value of the charge e on the electron
f. the mass of an electron (measured at rest)
g. the elapsed time on the wristwatch of a person moving between two given
events
h. the order ot elements in the periodic table
i. Newton’s First Law of Motion (“A particle initially at rest remains at rest,
and …”)
j. Maxwell’s equations that describe electromagnetic fields in a vacuum
k. the distance between two simultaneous events
74

75. Solution
•
•
•
•
•
•
•
•
•
THE SAME IN ALL FRAMES
c. numerical value of h
d. numerical value of c
e. numerical value of e
f. mass of electron (at rest)
g. wristwatch time between two
event (this is the proper time
interval between two event)
h. order of elements in the
periodic table
i. Newton’s First Law of Motion
j. Maxwell’s equations
k. distance between two
simultaneous events
•
•
MAY BE DIFFERENT IN
DIFFERENT FRAMES
a. time between two given
events
b. distance between two give
events
75

76. Relativistic Dynamics
•
•
Where does E=mc2 comes from?
By Einstein’s postulate, the observational law of
linear momentum must also hold true in all frames
of reference
m1u1
m 2u2
m1v1
m 2v2
Conservation of linear momentum classically means
m1u1 +m2u2 = m1v1 +m2v2
76

77. Classical definition of linear
momentum
•
Classically, one defines linear momentum as mass × velocity
•
Consider, in a particular reference frame where the object with a mass
m0 is moving with velocity v, then the momentum is defined (according
to classical mechanics) as
•
p = m0v.
•
If v = 0, the mass m0 is called the rest mass.
•
Similarly, in the other frame, (say the O’ frame), p’= m’v’
•
According to Newton’s mechanics, the mass m’(as seen in frame O’)
is the same as the mass m0 (as seen in O frame). There is no
distinction between the two.
•
In particular, there is no distinction between the rest77 and the
mass

78. Modification of expression of linear
momentum
•
However, simple analysis will reveal that in order to preserve the
consistency between conservation of momentum and the Lorentz
Transformation (to be discussed later), the definition of momentum has
to be modified to
• momentum = γm0v
•
where m0 is the rest mass (an invariant quantity).
•
A popular interpretation of the above re-definition of linear momentum
holds that the mass of an moving object, m, is different from its value
when it’s at rest, m0, by a factor of γ, i.e
• m = γm0
(however some physicists argue that this is actually not a correct
interpretation. For more details, see the article by Okun posted on the
course webpage. In any case, for pedagogical reason, we will stick to
the “popular interpretation” of the “relativistic mass”)
•
78

79. In other words…
•
•
•
•
In order to preserve the consistency between Lorentz
transformation of velocity and conservation of linear
momentum, the definition of 1-D linear momentum,
classically defined as
• pclassical = rest mass × velocity,
has to be modified to
pclassical → psr = “relativistic mass” × velocity
= mv = γm0v
where the relativisitic mass m = γm0 is not the same the rest
mass, m0
Read up the text for a more rigorous illustration why the
definition of classical momentum is inconsistent with LT
79

80. Pictorially…
I see the momentum of
M as p = mv=m0γv
I see M is at rest. Its mass
is m0, momentum, p’ = 0
O’
O
M
v
80

81. Two kinds of mass
•
•
•
Differentiate two kinds of mass: rest mass
and relativistic mass
m0 = rest mass = the mass measured in a
frame where the object is at rest. The rest
mass of an object must be the same in all
frames (not only in its rest frame).
Relativistic mass m = γ m0. The relativistic
mass is speed-dependent
81

82. Behaviour of pSR as compared to
pclassic
•
Classical momentum is
constant in mass, pclassic = m0v
•
Relativistic momentum is pSR =
m0γv
•
pSR / pclassic = γ  ∞ as v  c
•
In the other limit, v << c
pSR / pclassic = 1
82

83. Example
The rest mass of an electron is m0 = 9.11 x 10-31kg.
m0
If it moves with v = 0.75 c, what is its relativistic
momentum?
p = m0γu
Compare the relativistic p with that calculated
with classical definition
83

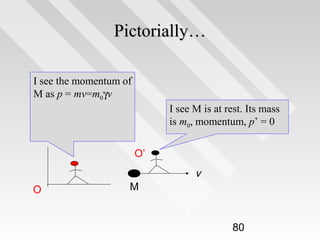
84. Solution
The Lorentz factor is
γ = [1-(v/c)2] -1/2 = [1-(0.75c/c)2] -1/2=1.51
• Hence the relativistic momentum is simply
p = γ m0 × 0.75c
•
•
= 1.51 × 9.11 × 10-31kg × 0.75 × 3 × 108 m/s
= 3.1 × 10-22 Ns
In comparison, classical momentum gives pclassical =
m0 × 0.75c = 2.5 × 10-22 Ns – about 34% lesser than
the relativistic value
84

85. Work-Kinetic energy theorem
•
Recall the law of conservation of mechanical
energy:
Work done by external force on a system,
W = the change in kinetic energy of the
system, ∆K
85

86. ∆Κ = K2 - K1
K1
K2
F
F
s
Conservation of mechanical energy: W = ∆K
W=Fs
The total energy of the object, E = K + U. Ignoring potential energy,
E of the object is solely in the form of kinetic energy. If K1 = 0, then
E = K2. But in general, U also needs to be taken into86
account for E.

87. In classical mechanics, mechanical energy (kinetic +
potential) of an object is closely related to its momentum and
mass
Since in SR we have redefined the classical mass and
momentum to that of relativistic version
mclass(cosnt, = m0)  mSR = m0γ
pclass = mclassv  pSR = (m0γ)v
we must also modify the relation btw work and energy so that
the law conservation of energy is consistent with SR
E.g, in classical mechanics, Kclass = p2/2m =mv2/2. However, this
relationship has to be supplanted by the relativistic version
Kclass = mv2/2  KSR = E – m0c2 = γm0c2 - m0c2
We shall derive K in SR in the following slides
87

88. Force, work and kinetic energy
•
When a force is acting on an object with rest mass
m0, it will get accelerated (say from rest) to some
speed (say v) and increase in kinetic energy from 0
to K
K as a function of v can be derived from first principle
based on the definition of:
Force, F = dp/dt,
work done, W = ∫ F dx,
and conservation of mechanical energy, ∆K = W
88

89. Derivation of relativistic kinetic
energy
Force = rate change of
momentum
x2
x2
x2
dp
 dp dx 
W = ∫ F dx = ∫
dx = ∫ 
÷dx
dt
dx dt 
x1 = 0
x1 = 0
x1 = 0 
x2
x2
v
Chain rule in
calculus
dp
dp
 dp dv 
= ∫
vdx = ∫ 
÷vdx = ∫ vdv
dx
dv dx 
dv
x1 = 0
x1 = 0 
0
dx
where, by definition,
is the velocity of the
v=
dt object 89

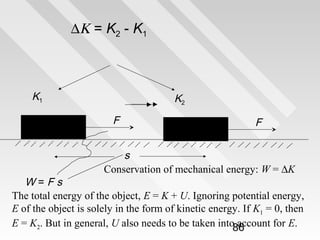
90. Explicitly, p = γ m0v,
Hence, dp/dv = d/dv (γm0v)
= m0 [v (dγ/dv) + γ]
= m0 [γ + (v2/c2) γ3] = m0 (1-v2/c2)-3/2
in which we have inserted the relation
dγ
d
=
dv dv
1
v
1
v 3
= 2
= 2γ
3/ 2
2
c  v2 
c
v
1− 2
1 − 2 ÷
c
 c 
 v 
W = m0 ∫ v 1 − 2 ÷
0
 c 
v
integrate
−3/ 2
2
dv
⇒ K = W = m0γ c − m0c = mc − m0c
2
2
2
90
2

91. K = m0γ c − m0c = mc − m0c
2
2
2
2
The relativistic kinetic energy of an object of rest
mass m0 traveling at speed v
E = mc2 is the total relativistic energy of an moving object
E0 = m0c2 is called the rest energy of the object.
Any object has non-zero rest mass contains energy E0 = m0c2
One can imagine that masses are ‘frozen energies in the
form of masses’ as per E0 = m0c2
The rest energy (or rest mass) is an invariant
91

92. •
Or in other words, the total relativistic energy of a
moving object is the sum of its rest energy and its
relativistic kinetic energy
E = mc = m0c + K
2
2
The (relativistic) mass of an moving object m is
larger than its rest mass m0 due to the contribution
from its relativistic kinetic energy – this is a pure
relativistic effect not possible in classical
mechanics
92

93. Pictorially
•
A moving object
Total relativistic energy =
kinetic energy + rest energy
E=mc2=K+E0
•
K=mc2 - E0 = ∆mc2
•
•
•
•
Object at rest
Total relativistic energy =
rest energy only (no
kinetic energy)
E=E0=m0c2
•
∆m
m0
m0
93
m=m0+∆m

94. Relativistic Kinetic Energy of an
electron
•
•
•
•
The kinetic energy increases without limit as the particle speed v
approaches the speed of light
In principle we can add as much kinetic energy as we want to a moving
particle in order to increase the kinetic energy of a particle without limit
What is the kinetic energy required to accelerate an electron to the speed
of light?
Exercise: compare the classical kinetic energy of an object, Kclas=m0v2/ 2 to
the relativistic kinetic energy, Ksr=(γ−1)m0c2. What are their difference?
94

95. Mass energy equivalence, E = mc2
E = mc2 relates the relativistic mass of an object to the total energy released
when the object is converted into pure energy
Example, 10 kg of mass, if converted into pure energy, it will be equivalent to
E = mc2 = 10 x (3 x108) 2 J = 9 x1017J - equivalent to a few tons of TNT
explosive
95

96. So, now you know how E=mc2
comes about…
96

97. Example 38-6: Energy of Fast
Particle
•
•
•
A particle of rest mass m0 moves so fast that
its total (relativistic) energy is equal to 1.1
times its rest energy.
(a) What is the speed v of the particle?
(b) What is the kinetic energy of the
particle?
97

98. Solution
(a)
• Rest energy E0 = m0c2
• We are looking for a speed such that the energy is 1.1 times
the rest energy.
• We know how the relativistic energy is related to the rest
energy via
• E = γE0 = 1.1E0
∀ ⇒ 1/ γ2 = 1/1.12 = 1/1.21 = 0.8264
• 1- v2/c2 = 0.8264
∀ ⇒ v2/c2 = 1- 0.8264 = 0.1736
∀ ⇒ v = 0.4166 2c
(b) Kinetic energy is K = E – E0 = 1.1E0 - E0 = 0.1E0 =0.1 m0c2
98

99. Reduction of relativistic kinetic
energy to the classical limit
•
The expression of the relativistic kinetic
energy
2
2
K = m0γ c − m0c
must reduce to that of classical one in the limit v/c
 0, i.e.
lim K relativistic =
v << c
p
2
2
classical
2m0
m0 v
(=
)
2
99

100. Expand γ with binomial expansion
•
For v << c, we can always expand γ in terms of
(v/c)2 as
−1/ 2
 v 
γ = 1 − 2 ÷
 c 
2
v2
v4
= 1 + 2 + terms of order 4 and higher
2c
c
K = mc − m0c = m0c (γ − 1)
 1 v 2
 m0 v 2

2
= m0 c 1 +
+ ... ÷− 1 ≈
2
2
 
 2 c
i.e., the relativistic kinetic energy reduces to
classical expression in the v << c limit 100
2
2
2

101. Exercise
•
•
•
Plot Kclass and Ksr vs (v/c)2 on the same graph for (v/c)
2
between 0 and 1.
Ask: In general, for a given velocity, does the
classical kinetic energy of an moving object larger
or smaller compared to its relativistic kinetic
energy?
In general does the discrepancy between the
classical KE and relativistic KE increase or
decrease as v gets closer to c?
101

102. 

1
K sr = m0 c 
− 1÷
 1− v / c 2
÷
( )


2
K
Kclass= m0c2 (v’/c)2 /2


1
2
K sr = m0 c
− 1÷
2
 1 − v′ / c
÷
(
)


Kclass(v= c) = m0c2/2
∆K
Kclass= m0c2 (v/c)2 /2
(v/c)2
0
(v’/c)2
1
Note that ∆K gets larger as v → c
102

103. Recap
•
Important formula for total energy, kinetic energy
and rest energy as predicted by SR:
E = total relativisitic energy;
m0 = rest mass;
m = relativistic mass;
E0 = rest energy ;
p = relativistic momentum,
K = relativistic momentum;
m = γ m0 ; p = γ m0v 2 ; K = γ m0c 2 − m0c 2 ; E0 = m0c 2 ; E = γ m0c 2 ;
103

104. Example
•
•
A microscopic particle
such as a proton can be
accelerated to extremely
high speed of v = 0.85c
in the Tevatron at
Fermi National Accelerator Laboratory
, US.
Find its total energy and
kinetic energy in eV.
104

105. Solution
•
•
•
•
•
•
Due to mass-energy equivalence, sometimes we
express the mass of an object in unit of energy
Proton has rest mass mp = 1.67 × 10-27kg
The rest mass of the proton can be expressed as
energy equivalent, via
mpc2 = 1.67×10-31kg × (3 × 108m/s)2
= 1.5×10-10 J
= 1.5 × 10-10 × (1.6x10-19)-1 eV
= 939,375,000 eV = 939 MeV
105

106. Solution
•
•
First, find the Lorentz factor, γ = 1.89
The rest mass of proton, m0c2, is 939 MeV
•
Hence the total energy is
E = mc2 = γ (m0c2)= 1.89 × 939 MeV = 1774 MeV
•
Kinetic energy is the difference between the total
relativistic energy and the rest mass,
K = E - m0c2= (1774 – 939) MeV = 835 MeV
106

107. Exercise
•
Show that the rest mass of an electron is
equivalent to 0.51 MeV
107

108. Conservation of Kinetic energy in
relativistic collision
•
Calculate (i) the kinetic energy of the
system and (ii) mass increase for a
completely inelastic head-on of two balls
(with rest mass m0 each) moving toward the
other at speed v/c = 1.5×10-6 (the speed of a
1.5
jet plane). M is the resultant mass after
collision, assumed at rest.
M
m0
v
v
108
m0

109. Solution
•
•
•
•
•
•
•
•
(i) K = 2mc2 - 2m0c2 = 2(γ−1)m0c2
(ii) Ebefore = Eafter ⇒ 2γ m0c2 = Mc2 ⇒ M = 2γ m0
Mass increase ∆M = M - 2m0 = 2(γ −1)m0
Approximation: v/c = …=1.5x10-6 ⇒ γ ≈ 1 + ½ v2/c2
(binomail expansion) ⇒ M ≈ 2(1 + ½ v2/c2)m0
Mass increase ∆M = M - 2m0
≈ (v2/c2)m0 = (1.5x10-6)2m0
Comparing K with ∆Mc2: the kinetic energy is not lost
in relativistic inelastic collision but is converted into the
mass of the final composite object, i.e. kinetic energy is
conserved
In contrast, in classical mechanics, momentum is
conserved but kinetic energy is not in an inelastic
109
collision

110. Relativistic momentum and
relativistic Energy
In terms of relativistic momentum, the relativistic
total energy can be expressed as followed
2
2
v
c p
E =γ m c ;p =γ m v ⇒ 2 = 2
c
E
2
2
2 4
0
2
2
2 2
0
2
2
2
m0 c 4  m0 c 4 E 2 
2
⇒ E 2 = γ 2 m0 c 4 =
= 2 2 2 ÷
2
v
 E −c p 
1− 2
c
E = p c +m c
2
2 2
2 4
0
Energy-momentum
invariance
110

111. Invariance in relativistic dynamics
•
•
•
•
Note that E2 - p2c2 is an invariant, numerically equal to
(m0c2)2
i.e., in any dynamical process, the difference between the
total energy squared and total momentum squared of a
given system must remain unchanged
In additional, when observed in other frames of reference,
the total relativistic energy and total relativistic momentum
may have different values, but their difference, E2 - p2c2,
must remain invariant
Such invariance greatly simplify the calculations in
relativistic dynamics
111

112. •
•
Example: measuring pion mass
using conservation of momentumenergy
pi meson decays into a muon + massless neutrino
If the mass of the muon is known to be 106 MeV/c2, and
the kinetik energy of the muon is measured to be 4.6 MeV,
find the mass of the pion
112

113. Solution
Relationship between Kinetic energy and momentum:
2
2
2
Eµ = pµ c 2 + mµ c 4
Conservation of relativistic energy: Eπ = Eµ + Eν
2
⇒ mπ c 2 = mµ c 4 + c 2 pµ 2 + mν2c 4 + c 2 pν 2
2
⇒ mπ c = mµ c 2 + pµ 2 + pµ
Momentum conservation: pµ = pν
Also, total energy = K.E. + rest energy
2
Eµ = K µ + mµ c 2 ⇒ Eµ = ( K µ + mµ c 2 )
2
2
2
2
But Eµ = pµ c 2 + mµ c 4
2
2
2
⇒ Eµ = pµ c 2 + mµ c 4 = ( K µ + mµ c 2 ) ;
2
pµ c =
(K
µ
+ mµ c
)
2 2
2
2
− mµ c 4 = K µ + 2 K µ mµ c 2
113

114. Plug p c = ( K µ + mµ c
2 2
µ
)
2 2
2
− mµ c 4 into
2
mπ c 2 = mµ c 4 + c 2 pµ 2 + cpµ
( K + m c 2 ) 2 − m 2 c 4  +
= mµ c +  µ
µ
µ



2 4
= ( K µ + mµ c 2 ) +
(K
2
µ
(K
µ
+ mµ c
)
2 2
2
− mµ c 4
+ 2 K µ mµ c 2 )

106MeV 2 
=  4.6MeV+
c ÷+
2
c


 106MeV  2
( 4.6MeV ) + 2 ( 4.6MeV ) 
÷c
2
c


2
= 111MeV + 996MeV=143MeV
114

115. Observing an event from lab frame and
rocket frame
115

116. Lorentz Transformation
•
•
•
•
All inertial frames are equivalent
Hence all physical processes analysed in one frame
can also be analysed in other inertial frame and yield
consistent results
Any event observed in two frames of reference must
yield consistent results related by transformation laws
Specifically such a transformation law is required to
related the space and time coordinates of an event
observed in one frame to that observed from the other
116

117. Different frame uses different
notation for coordinates
•
•
•
O' frame uses {x',y',z';t'} to denote the
coordinates of an event, whereas O frame uses
{x,y,z;t}
How to related {x',y',z',t'} to {x,y,z;t}?
In Newtonian mechanics, we use Galilean
transformation
117

118. Two observers in two inertial frames
with relative motion use different
notation
I measures the coordinates of
M as {x,t};
I see O’ moving with a
velocity +v
+v
I measures the coordinates
of M as {x’,t’}
I see O moving with a
velocity -v
-v
Object M
O
x
x’
O’
118

119. Galilean transformation
(applicable only for v<<c)
•
•
•
For example, the spatial coordinate of the
object M as observed in O is x and is being
observed at a time t, whereas according to O’,
the coordinate for the space and time
coordinates are x’ and t’. At low speed v <<c,
the transformation that relates {x',t'} to {x,t} is
given by Galilean transformation
{x'=x-vt, t' = t} (x' and t' in terms of x,t)
{x = x' + vt, t = t'} (x and t in terms of x',t')
119

120. •
•
•
•
•
•
•
Illustration on Galilean transformation
of {xthe=x-vt,hence= t}
' O frame, t' the coordinate of the object M
Assume object M is at rest in
in O frame is fixed at x
Initially, when t = t’ = 0, O and O’ overlap
O’ is moving away from O at velocity +v
The distance of the origin of O’ is increasing with time. At time t (in O frame),
the origin of O’ frame is at an instantaneous distance of + vt away from O
In the O’ frame the object M is moving away with a velocity – v (to the left)
Obviously, in O’ frame, the coordinate of the object M, denoted by x’, is timedependent, being x’ = x – vt
In addition, under current assumption (i.e. classical viewpoint) the rate of time
flow is assumed to be the same in both frame, hence t = t’
+v
vt
O
Object M
x (fixed)
O’
x’ (not fixed, time 120
dependent)

121. However, GT contradicts the SR
postulate when v approaches the
speed of light, hence it has to be
supplanted by a relativistic version
of transformation law when near-tolight speeds are involved:
Lorentz transformation
(The contradiction becomes more
obvious if GT on velocities, rather
than on space and time, is considered)
121

122. Galilean transformation of velocity
(applicable only for ux,v << c)
•
•
•
•
Now, say object M is moving as a velocity of v wrp to the lab
frame O
What is the velocity of M as measured by O’?
Differentiate x’ = x – vt wrp to t (=t’), we obtain
d(x’)/dt’ = d(x – vt)/dt = d(x)/dt – v
⇒
ux’ = ux – v
ux(as seen by O); ux’ (as seen by O’)
Object M
I see M moving with
velocity ux
+v
O
O’
I see M moving with
velocity ux’
122

123. If applied to light Galilean transformation of
velocity
contradictsa the SR Postulate
• Consider another case, now, photon (particle of light) observed from
•
•
•
different frames
A photon. being a massless particle of light must move at a speed ux = c
when observed in O frame
However Galilean velocity addition law ux’ = ux – v, if applied to the
photon, says that in O’ frame, the photon shall move at a lower speed of
ux’ = ux – v = c – v
This is a contradiction to the constancy of light speed in SR
I see the photon is moving photon
with a velocity ux = c
ux = c(as seen by
O); ux’ = c – v (as
seen by O’)
O
+v
O’
I see the photon is
moving with a
velocity ux’ = c –
v, this couldn’t be
right
123

124. Conclusion
•
•
•
GT (either for spatial, temporal or velocity)
cannot be applicable when dealing with
object moving near or at the speed of light
It has to be supplanted by a more general
form of transformation – Lorentz
transformation, LT
LT must reduce to GT when v << c.
124

125. Derivation of Lorentz transformation
Our purpose is to find the general transformation that relates { x,t} to {x’,t’ }
125
(applicable not only for v<<c but also for v≈c)

126. Read derivation of LT from the texts
•
•
•
Brehm and Mullin
Krane
Serway, Mayer and Mosses
126

127. Derivation of Lorentz transformation
•
•
•
•
Consider a rocket moving with a speed v (O' frame) along the
xx' direction wrp to the stationary O frame
A light pulse is emitted at the instant t' = t = 0 when the two
origins of the two reference frames coincide
The light signal travels as a spherical wave at a constant speed c
in both frames
After in time interval of t, the origin of the wave centred at O
has a radius r = ct, where r 2 = x2 + y2 + z2
127

128. Arguments
•
•
•
•
∀
•
∀
•
•
From the view point of O', after an interval t‘ the origin of the wave,
centred at O' has a radius:
r' = ct' , (r’ )2 = (x’)2 + (y’ )2 + (z’ )2
y'=y, z' = z (because the motion of O' is along the xx’) axis – no change
for y,z coordinates (condition A)
The transformation from x to x’ (and vice versa) must be linear, i.e. x’  x
(condition B)
Boundary condition (1): If v = c, from the viewpoint of O, the origin of O’
is located on the wavefront (to the right of O)
⇒ x ’ = 0 must correspond to x = ct
Boundary condition (2): In the same limit, from the viewpoint of O’, the
origin of O is located on the wavefront (to the left of O’)
⇒ x = 0 corresponds to x’ = -ct’
Putting everything together we assume the transformation that relates x’
to {x, t} takes the form x’ = k(x - ct) as this will fulfill all the conditions
(B) and boundary condition (1) ; (k some proportional constant to be
determined)
Likewise, we assume the form x = k(x’ + ct ’) to relate x to {x ’, t‘ } as this
is the form that fulfill all the conditions (B) and boundary condition (2)
128

129. •
•
•
•
•
•
Illustration of Boundary
condition (1)
x = ct (x’= ct’) is defined as the x-coordinate (x’-coordinate ) of the wavefront in the O (O’) frame
Now, we choose O as the rest frame, O’ as the rocket frame. Furthermore, assume O’ is moving
away to the right from O with light speed, i.e. v = +c
Since u = c, this means that the wavefront and the origin of O’ coincides all the time
For O, the x-coordinate of the wavefront is moving away from O at light speed; this is tantamount to
the statement that x = ct
From O’ point of view, the x’-coordinate of the wavefront is at the origin of it’s frame; this is
tantamount to the statement that x’ = 0
Hence, in our yet-to-be-derived transformation, x’ = 0 must correspond to x = ct
The time now is t.
The x-coordinate of the
wavefront is located at the
distance x = ct, coincident
with O’ origin
v=c
O
r=ct
The time now is
t’. The x’coordinate of
the wavefront is
located at my
frame’s origin,
x’ = 0
O’
wavefront
129

130. Permuting frames
•
•
•
Since all frames are equivalent, physics analyzed
in O’ frame moving to the right with velocity +v is
equivalent to the physics analyzed in O frame
moving to the left with velocity –v
Previously we choose O frame as the lab frame
and O’ frame the rocket frame moving to the right
(with velocity +v wrp to O)
Alternatively, we can also fix O’ as the lab frame
and let O frame becomes the rocket frame moving
to the left (with velocity –v wrp to O’)
130

131. •
•
•
•
Illustration of Boundary
condition (2)
Now, we choose O’ as the rest frame, O as the rocket frame. From O’ point of view, O
is moving to the left with a relative velocity v = - c
From O’ point of view, the wavefront and the origin of O coincides. The x’-coordinate
of the wavefront is moving away from O’ at light speed to the left; this is tantamount to
the statement that x’ = -ct’
From O point of view, the x-coordinate of the wavefront is at the origin of it’s frame;
this is tantamount to the statement that x = 0
Hence, in our yet-to-be-derived transformation, x = 0 must correspond to x’ = - ct’
wavefront
v=- c
The time now is t.
The x-coordinate of the
wavefront is located at my
frame’s origin, x = 0
O
r=ct
O’
The time now is t’.
The x’-coordinate
of the wavefront is
located at the
distance x’ = -ct’,
coincident with O
origin
131

132. Finally, the transformation obtained
•
•
•
•
•
We now have
r = ct, r2 = x2 + y2 + z2; y'=y, z' = z ;x = k(x’ + ct’);
r’ = ct’, r’ 2 = x’2 + y’2 + z’2; x’ = k(x - ct);
With some algebra, we can solve for {x',t'} in terms of {x,t} to obtain the
desired transformation law (do it as an exercise)
The constant k turns out to be identified as the Lorentz factor, γ
x' =
x − vt
2
v
1−  ÷
c
= γ ( x − vt )
t'=
t − ( v / c2 ) x
2
v
1−  ÷
c
= γ t − (v / c 2 ) x 


(x’ and t’ in terms of x,t)
132

133. Space and time now becomes stateof-motion dependent (via γ)
•
•
•
Note that, now, the length and time interval
measured become dependent of the state of
motion (in terms of γ) – in contrast to Newton’s
classical viewpoint
Lorentz transformation reduces to Galilean
transformation when v << c (show this
yourself)
i.e. LT  GT in the limit v << c
133

134. How to express {x, t} in terms of {x’, t’ }?
•
We have expressed {x',t'} in terms of {x,t }
as per
x' =
•
x − vt
2
v
1−  ÷
c
= γ ( x − vt )
t'=
t − ( v / c2 ) x
2
v
1−  ÷
c
= γ  t − (v / c 2 ) x 


Now, how do we express {x, t } in terms of
{x’, t’ }?
134

135. Simply permute the role of x and x’
and reverse the sign of v
t ↔ t ', x ↔ x ', v → −v
x ' = γ ( x − vt ) → x = γ ( x '+ vt ')
t ' = γ t − (v / c 2 ) x  → t = γ t '+ (v / c 2 ) x '




The two transformations above are equivalent; use which is
appropriate in a given question
135

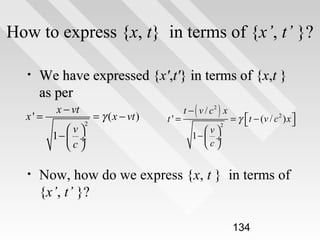
136. Length contraction
Consider the rest length of a ruler as measured in frame O’ is
•
L’ = ∆x’ = x’2 - x’1 (proper length) measured at the same
instance in that frame (t’2 = t’1)
•
What is the length of the rule as measured by O?
•
The length in O, L, according the LT can be deduced as
followed:
L’ = ∆x’ = x’2 - x’1 = γ [(x2 - x1) – v(t2 -t1)]
•
The length of the ruler in O, L, is simply the distance btw x2
and x1 measured at the same instance in that frame (t2 = t1).
Hence we have
•
L’ = γ L
•
where L = is the improper length.
•
As a consequence, we obtain the relation between the proper
length measured by the observer at rest wrp to the ruler and
that measured by an observer who is at a relative motion wrp to
the ruler:
136
•

137. Moving rulers appear shorter
L’ = γ L
•
•
•
•
•
L’ is defined as the proper length = length of and object
measured in the frame in which the object is at rest
L is the length measured in a frame which is moving wrp
to the ruler
If an observer at rest wrp to an object measures its length
to be L’ , an observer moving with a relative speed u wrp to
the object will find the object to be shorter than its rest
length by a factor 1 / γ
i.e., the length of a moving object is measured to be shorter
than the proper length – hence “length contraction”
In other words, a moving rule will appear shorter!!
137

138. Example of a moving ruler
•
•
Consider a meter rule is carried
on board in a rocket (call the
rocket frame O’)
An astronaut in the rocket
measure the length of the ruler.
Since the ruler is at rest wrp to
the astronaut in O’, the length
measured by the astronaut is the
proper length, Lp = 1.00 m, see (a)
Now consider an observer on the
lab frame on Earth. The ruler
appears moving when viewed by
the lab observer. If the lab
observer attempts to measure the
ruler, the ruler would appear
shorter than 1.00m
The ruler is at moving at a
speed v when I measure it. Its
length is L = 0.999 m
The ruler is at rest when
I measure it. Its length is
Lp = 1.00 m
138

139. RE 38-11
•
What is the speed v of a passing rocket in
the case that we measure the length of the
rocket to be half its length as measured in a
frame in which the rocket is at rest?
139

140. Length contraction only happens
along the direction of motion
Example: A spaceship in the form of a triangle flies by an
oberver at rest wrp to the ship (see fig (a)), the distance x
and y are found to be 50.0 m and 25.0 m respectively.
What is the shape of the ship as seen by an observer who
sees the ship in motion along the direction shown in fig
(b)?
140

141. Solution
•
•
•
The observer sees the horizontal length of the ship to
be contracted to a length of
L = Lp/γ = 50 m√(1 – 0.9502) = 15.6 m
The 25 m vertical height is unchanged because it is
perpendicular to the direction of relative motion
between the observer and the spaceship.
141

142. Similarly, one could also derive time
dilation from the LT
Do it as homework
142

143. An interesting story book to read
•
Mr. Thompkins’s in paper back, by George
Gamow.
143

144. •
What is the velocities of the ejected
stone?
Imagine you ride on a rocket moving ¾ c
wrp to the lab. From your rocket you launch
a stone forward at ½ c, as measured in your
rocket frame. What is the speed of the stone
observed by the lab observer?
¾ c, wrp to lab
The speed of the stone
as I measure it is…
½ c, wrp to the
rocket
144

145. •
Adding relativistic velocities using
Galilean (which is valid at low speed regime v <<
transformation
According to GT of velocity
c),
•
the lab observer would measure a velocity of ux=ux’+ v = ½ c + ¾ c
•
= 1.25 c for the ejected stone.
However, in SR, c is the ultimate speed and no object can ever exceed
this ultimate speed limit
So something is no right here…Galilean addition law is no more valid
to handle addition of relativistic velocities (i.e. at speed near to c)
•
•
¾ c, wrp to lab
If I use GT, the speed of the stone
as is 1.25 c!!! It couldn’t be right
½ c, wrp to the
rocket
145

146. Relativity of velocities
•
•
The generalised transformation law of velocity used for addition
of relativistic velocities is called Lorentz transformation of
velocities, derived from the Lorentz transformation of spacetime
Our task is to relate the velocity of the object M as observed by
O’ (i.e. ux’) to that observed by O (i.e. ux).
I see the object M is moving
with a velocity ux, I also see
O’ is moving with a velocity
+v
O
ux (as seen by O); ux’ (as
seen by O’)
A moving Object M
+v
O’
I see the object M is
moving with a
velocity ux’
146

147. Relativity of velocities
•
•
Consider an moving object being observed by two observers,
one in the lab frame and the other in the rocket frame
We could derive the Lorentz transformation of velocities by
taking time derivative wrp to the LT for space-time, see next
slide
I see the object M is moving
with a velocity ux, I also see
O’ is moving with a velocity
+v
O
ux (as seen by O); ux’ (as
seen by O’)
A moving Object M
+v
O’
I see the object M is
moving with a
velocity ux’
147

148. Derivation of Lorentz transformation
of velocities
•
By definition, ux = dx/dt, u’x = dx’/dt’
•
The velocity in the O’ frame can be obtained
by taking the differentials of the Lorentz
transformation
x ' = γ ( x − vt ) t ' = γ t − (v / c ) x 


v
dx ' = γ (dx − vdt ), dt ' = γ (dt − 2 dx)
c
2
148

149. Combining
dx ' γ (dx − vdt )
u =
=
dt ' γ (dt − v dx)
2
c
u −v
'
x
=
x
dt 
 dx
dt  − v ÷
dt 
 dt
=
 dt v dx 
dt  − 2
÷
 dt c dt 
vu x
1− 2
c
where we have made used of the definition ux
= dx/dt
149

150. Comparing the LT of velocity with
that of GT
Lorentz transformation of velocity:
dx ' u x − v
u 'x =
=
dt ' 1 − u x v
c2
Galilean transformation of velocity:
u 'x = u x − v
LT reduces to GT in the limit
u x v << c
2
150

151. •
Please try to make a clear distinction
among the definitions of various
velocities, i.e. ux , u’x , v so that you wont
get confused
151

152. LT is consistent with the
constancy of speed of light
•
•
•
In either O or O’ frame, the speed of light seen must be
the same, c. LT is consistent with this requirement.
Say object M is moving with speed of light as seen by
O, i.e. ux = c
According to LT, the speed of M as seen by O’ is
u 'x =
•
ux − v
c −v c −u
c−v
=
=
=
=c
uv
cv
v 1
1 − x2 1 − 2 1 −
( c − v)
c
c c
c
That is, in either frame, both observers agree that the
speed of light they measure is the same, c = 3 × 108m/s
152

153. •
How to express ux in terms of
ux’?
Simply permute v with – v and change the
role of ux with that of ux’:
u x → u ' x , u ' x → u x , v → −v
ux − v
u 'x + v
u 'x =
→ ux =
ux v
u 'x v
1− 2
1+ 2
c
c
153

154. Recap: Lorentz transformation
relates
{x’,t’}  {x,t}; u’x ux
x ' = γ ( x − vt )
t − (v / c 2 ) x 
t'=γ 

ux − v
u 'x =
uxv
1− 2
c
x = γ ( x '+ vt ')
t = γ t '+ (v / c 2 ) x '


u 'x + v
ux =
u 'x v
1+ 2
c
154

155. RE 38-12
•
A rocket moves with speed 0.9c in our lab
frame. A flash of light is sent toward from
the front end of the rocket. Is the speed of
that flash equal to 1.9 c as measured in our
lab frame? If not, what is the speed of the
light flash in our frame? Verify your answer
using LT of velocity formula.
155

156. Example (relativistic velocity
addition)
•
Rocket 1 is approaching rocket 2 on a
head-on collision course. Each is moving at
velocity 4c/5 relative to an independent
observer midway between the two. With
what velocity does rocket 2 approaches
rocket 1?
156

157. Diagramatical translation of the
question in text
v
Note: c.f. in GT, their relative speed would just be 4c/5 + 4c/5 = 1.6 c
which violates constancy of speed of light postulate. See how LT
handle this situation:
157

158. •
•
•
•
•
•
•
Choose the observer in the middle as in the stationary frame, O
Choose rocket 1 as the moving frame O’
Call the velocity of rocket 2 as seen from rocket 1 u’x. This is the quantity we
are interested in
Frame O' is moving in the +ve direction as seen in O, so v = +4c/5
The velocity of rocket 2 as seen from O is in the
-ve direction, so ux = - 4c/5
Now, what is the velocity of rocket 2 as seen from frame O', u ’x = ?
(intuitively, u ’x must be in the negative direction)
v
158

159. Using LT:
 4c   4c 
 − ÷−  + ÷
u −v
40
5   5 
u 'x = x
= 
=− c
uv
41
 4c   4c 
1 − x2
− ÷ + ÷

c
5  5 
1− 
c2
v
i.e. the velocity of rocket 2 as seen from rocket 1 (the moving
frame, O’) is –40c/41, which means that O’ sees rocket 2
moving in the –ve direction (to the left in the picture), as
expected.
159

160. Doppler Shift
•
R.I.Y
160

161. 161