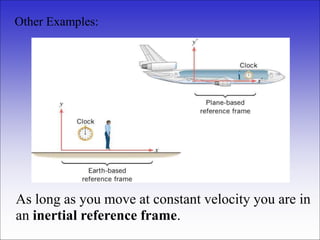
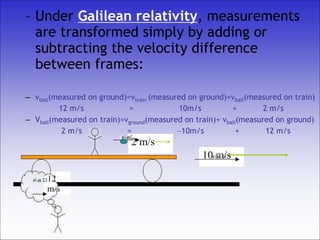
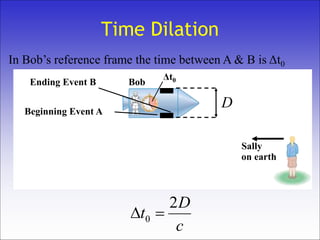
The document discusses the principles of relativity developed by Albert Einstein, emphasizing key concepts such as the Galilean relativity principle and postulates of special relativity. It covers the effects of relativistic phenomena, including time dilation and length contraction, and describes how observations differ between moving observers. Einstein's thought experiments and conclusions about the invariance of the speed of light further illustrate the fundamental changes in understanding motion and time.

1. Relativity
by
Albert Einstein
Prepared by:
Sir Antonio Salvador Jr.

2. The Relativity Principle
Galileo Galilei
1564 - 1642
The Ptolemaic
Model
The Copernican
Model
Problem: If the earth were moving
wouldn’t we feel it?

3. A coordinate system moving at a
constant velocity is called an inertial
reference frame.
The Galilean Relativity Principle:
All physical laws are the same in all inertial reference
frames.

4. Other Examples:
As long as you move at constant velocity you are in
an inertial reference frame.

5. Galilean Relativity
– “Relativity” refers in general to the way
physical measurements made in a given
inertial frame are related to
measurements in another frame.
– An inertial observer is one whose rest
frame is inertial.
– A quantity is invariant if all inertial
observers obtain the same value.

6. – Under Galilean relativity, measurements
are transformed simply by adding or
subtracting the velocity difference
between frames:
– vball(measured on ground)=vtrain (measured on ground)+vball(measured on train)
12 m/s = 10m/s + 2 m/s
– Vball(measured on train)=vground(measured on train)+ vball(measured on ground)
2 m/s = 10m/s + 12 m/s
10 m/s
2 m/s
12
m/s

7. Electromagnetism
A wave solution traveling at the speed of
light
c = 3.00 x 108 m/s
Maxwell: Light is an EM wave!
Problem: The equations don’t tell what
light is traveling with respect to
James Clerk
Maxwell 1831 -
1879

8. Einstein’s Approach to Physics
Albert Einstein
1879 - 1955
1. (Thought) Experiments
E.g., if we could travel next to a light
wave, what would we see?
2. “The Einstein Principle”:
If two phenomena are indistinguishable
by experiments then they are the same
thing.

9. Einstein’s Approach to Physics
2. “The Einstein Principle”:
If two phenomena are indistinguishable
by experiments then they are the same
thing.
A magnet moving A coil moving towards
a magnet
Both produce the same current
Implies that they are the same phenomenon
towards a coil
Albert Einstein
1879 - 1955
curren
t
curren
t

10. Einstein’s Approach to Physics
1. Gedanken (Thought) Experiments
E.g., if we could travel next to a light
wave, what would we see?
c
c
We would see an EM wave frozen in space next to us
Problem: EM equations don’t predict stationary waves
Albert Einstein
1879 - 1955

11. Electromagnetism
Another Problem: Every experiment measured the speed of
light to be c regardless of motion
The observer on the
ground should
measure the speed of
this wave as c + 15
m/s
Both observers actually measure the speed of this wave as
c!

12. Special Relativity Postulates
• The Relativity Postulate: The laws of physics are the
same in every inertial reference frame.
• The Speed of Light Postulate: The speed of light in
vacuum, measured in any inertial reference frame, always
has the same value of c.
Einstein: Start with 2 assumptions & deduce all else
This is a literal interpretation of
the EM equations

13. Special Relativity Postulates
Looking through Einstein’s eyes:
Both observers (by
the postulates)
should measure the
speed of this wave
as c
Consequences:
• Time behaves very differently than expected
• Space behaves very differently than expected

14. Einstein’s Special Relativity
1,000,000 ms-1
0 ms-1
300,000,000 ms-1
 Both spacemen measure the speed of the approaching ray of light.
 How fast do they measure the speed of light to be?

15. Einstein’s Special Relativity
• Stationary man
– 300,000,000 ms-1
• Man travelling at 1,000,000 ms-1
– 301,000,000 ms-1?
– Wrong!
• The Speed of Light is
the same for all observers

16. Three effects
• 3 strange effects of special relativity
– Lorentz Transformations
– Relativistic Doppler Effect
– Headlight Effect

17. Lorentz Transformations
■ Light from the top of the bar has further to travel.
■ It therefore takes longer to reach the eye.
■ So, the bar appears bent.
■ Weird!

18. Doppler Effect
• The pitch of the siren:
– Rises as the ambulance approaches
– Falls once the ambulance has passed.
• The same applies to light!
– Approaching objects appear blue (Blue-shift)
– Receding objects appear red (Red-shift)

19. Headlight effect
• Beam becomes focused.
• Same amount of light concentrated in a
smaller area
• Torch appears brighter!
V

20. Warp
• Program used to visualise the three effects
Demo . . .

21. Fun stuff
• Website:
http://www.adamauton.com/warp/
Eiffel Tower Stonehenge

22. Time Dilation
One consequence: Time Changes
Equipment needed: a light clock and a fast space ship.

23. Time Dilation
In Bob’s reference frame the time between A & B is Δt0
Sally
on earth
Bob
Beginning Event A
Ending Event B
c
D
t
2
0 
D
Δt0

24. Bob
Time Dilation
In Sally’s reference frame the time between A & B is Δt
Bob
A BSally
on earth
2
2 2 2
2 2 2
2
v t
s D L D
 
     
 
Length of path for the light ray:
c
s
t
2
and
Δt

25. Time Dilation
2
2 2 2
2 2 2
2
v t
s D L D
 
     
 
Length of path for the light ray:
c
s
t
2
and
Solve for Δt:
22
/1
/2
cv
cD
t

 cDt /20 
Time measured
by Bob
22
0
/1 cv
t
t




26. Time Dilation
22
0
/1 cv
t
t



Δt0 = the time between A &
B measured by Bob
Δt = the time between A &
B measured by Sally
v = the speed of one
observer relative to the
other
Time Dilation = Moving clocks slow down
If Δt0 = 1s, v = .999 c then: s500
999.1
s1
2


t

27. Time Dilation
• Bob’s watch always displays his proper time
• Sally’s watch always displays her proper time
How do we define time?
The flow of time each observer experiences is measured by
their watch – we call this the proper time
• If they are moving relative to each other they will not
agree

28. Time Dilation
A Real Life Example: Lifetime of muons
Muon’s rest lifetime = 2.2x10-6 seconds
Many muons in the upper atmosphere (or in the laboratory)
travel at high speed.
If v = 0.999 c. What will be its average lifetime as seen by
an observer at rest?
s101.1
999.1
s102.2
/1
3
2
6
22
0 








cv
t
t

29. Length Contraction
Bob’s reference frame:
The distance measured by the spacecraft is shorter
Sally’s reference frame:
Sally
Bob
0
0
LL
v
t t
 
 
The relative speed v is the
same for both observers:
22
0
/1 cv
t
t



22
0 /1 cvLL 

30. -END-