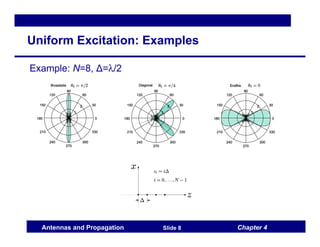
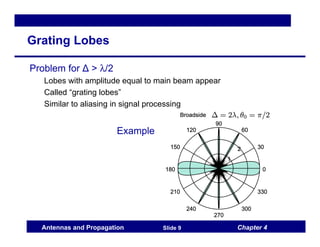
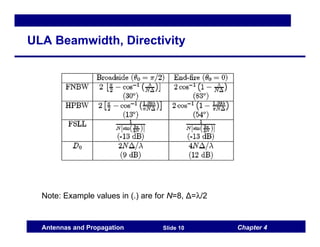
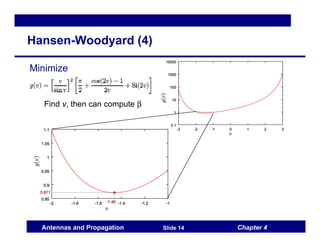
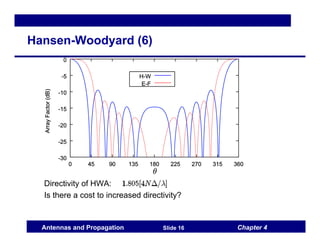
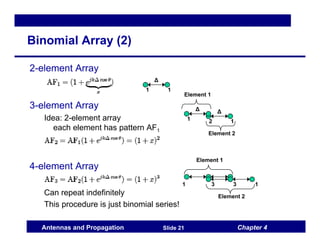
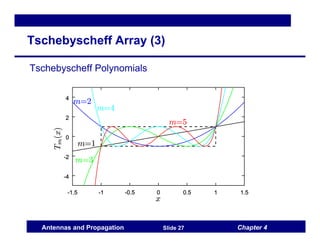
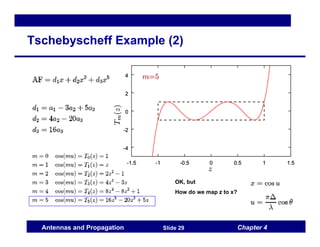
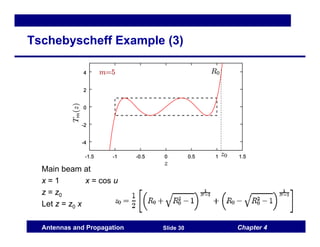
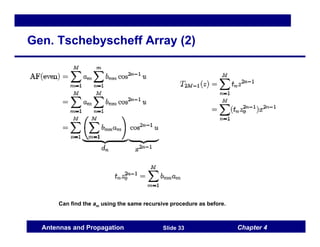
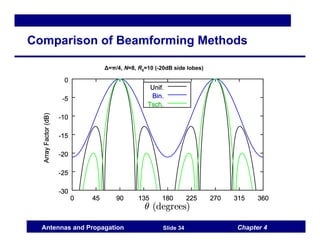
This document discusses antenna arrays and beamforming techniques. It describes how antenna arrays combine multiple antenna elements to provide more flexibility in transmitting and receiving signals compared to a single antenna. Key techniques covered include beamforming through phase and amplitude control of array elements, as well as diversity and spatial multiplexing. The document also summarizes common array configurations like uniform linear arrays and methods for designing the array factor, such as uniform excitation, binomial arrays, and Tschebyscheff arrays.

1. Chapter 5: Antenna Arrays
Antennas and Propagation

2. Chapter 4
Antennas and Propagation Slide 2
5 Antenna Arrays
Advantage
Combine multiple antennas
More flexibility in transmitting / receiving signals
Spatial filtering
Beamforming
Excite elements coherently (phase/amp shifts)
Steer main lobes and nulls
Super-Resolution Methods
Non-linear techniques
Allow very high resolution for direction finding

3. Chapter 4
Antennas and Propagation Slide 3
5 Antenna Arrays (2)
Diversity
Redundant signals on multiple antennas
Reduce effects due to channel fading
Spatial Multiplexing (MIMO)
Different information on multiple antennas
Increase system throughput (capacity)

4. Chapter 4
Antennas and Propagation Slide 4
General Array
Assume we have N elements
pattern of ith antenna
Total pattern
Identical antenna elements
“Pattern Multiplication”
Element Factor Array Factor

5. Chapter 4
Antennas and Propagation Slide 5
Uniform Linear Array (ULA)
Place N elements on the z-axis
Uniform spacing Δ

6. Chapter 4
Antennas and Propagation Slide 6
Uniform Excitation
Apply equal amplitude to elements
(different phases only)
Recall:

7. Chapter 4
Antennas and Propagation Slide 7
Uniform Excitation (2)
Note: sin(Nx)/sin(x) behaves
like Nsinc(x)
Maximum occurs for θ= θ0
If we center array about z=0, and normalize
Normalize input power with
additional elements for θ= θ0, sin(Nx)/sin(x) goes to N
Result: Steers a beam in direction
θ= θ0 that has amplitude N1/2
compared to single element
“Array Gain”

8. Chapter 4
Antennas and Propagation Slide 8
Uniform Excitation: Examples
Example: N=8, Δ=λ/2

9. Chapter 4
Antennas and Propagation Slide 9
Grating Lobes
Problem for Δ > λ/2
Lobes with amplitude equal to main beam appear
Called “grating lobes”
Similar to aliasing in signal processing
Example

10. Chapter 4
Antennas and Propagation Slide 10
ULA Beamwidth, Directivity
Note: Example values in (.) are for N=8, Δ=λ/2

11. Chapter 4
Antennas and Propagation Slide 11
Hansen-Woodyard (HWA)
Idea
End-fire excitation has a fat main lobe
Simple coherent excitation not optimal solution for directivity
HWA: do direct maximization
Analysis
Array factor for N elements and progressive phase shift β
Max max AF = 1

12. Chapter 4
Antennas and Propagation Slide 12
Hansen-Woodyard (2)
Consider small
Means scan angle on “main beam”
Progressive phase shift

13. Chapter 4
Antennas and Propagation Slide 13
Hansen-Woodyard (3)
Radiation intensity: proportional to |AF|2
In beam direction, θ=0, U(θ) is
Normalize U to make unity at θ=0. Call new function U′(θ)
Directivity found as D0=4πUmax/Prad = Umax/U0, with
How do we maximize D0?

14. Chapter 4
Antennas and Propagation Slide 14
Hansen-Woodyard (4)
Minimize
Find v, then can compute β

15. Chapter 4
Antennas and Propagation Slide 15
Hansen-Woodyard (5)
vmin = -1.46

16. Chapter 4
Antennas and Propagation Slide 16
Hansen-Woodyard (6)
Directivity of HWA:
Is there a cost to increased directivity?

17. Chapter 4
Antennas and Propagation Slide 17
Non-Uniform Excitation
Increased Flexibility
Weights are general
Similar to a filter synthesis problem
Example methods
Binomial Array
Similar to “maximally flat” filter
No side lobes for Δ < λ/2
Tschebyscheff Array
Similar to “equiripple” filter
Produces smallest beamwidth
for given sidelobe level

18. Chapter 4
Antennas and Propagation Slide 18
Symmetric Array
Antennas placed symmetrically on ±z axis
(Also same excitation)
Odd number of elements:
put two copies of center element (for two sides)
Amplitude on true center
element is 2a1

19. Chapter 4
Antennas and Propagation Slide 19
Symmetric Array (2)
Array factors are
Example Methods
Binomial array
Derive based on heuristic argument
Tschebyscheff array
Use direct synthesis procedure

20. Chapter 4
Antennas and Propagation Slide 20
Binomial Array
2-element Array
Plot of AF1 = 1 + x
Has no side-lobes for Δ < λ/2
Idea to make more dir.
Successively superimpose
pairs of arrays
Generates AF = (AF1)M
Δ

21. Chapter 4
Antennas and Propagation Slide 21
Binomial Array (2)
2-element Array
3-element Array
Idea: 2-element array
each element has pattern AF1
4-element Array
Can repeat indefinitely
This procedure is just binomial series!
Δ
Δ
Element 1
Element 2
1 2 1
Δ
1 1
1 3 3 1
Element 1
Element 2

22. Chapter 4
Antennas and Propagation Slide 22
Binomial Array (3)
Coefficients
Also given by Pascal’s triangle

23. Chapter 4
Antennas and Propagation Slide 23
Binomial Array (4)
Advantage
No side lobes
Disadvantages
Wide main lobe
High variation in weights

24. Chapter 4
Antennas and Propagation Slide 24
General Array Synthesis
Procedure
Expand AF in a (cosine) power series
AF is a polynomial in x, where x=cos u
Choose a desired pattern shape
(polynomial of same order)
Equate coefficients of polynomials
⇒ yields weights on arrays
Example
Dolph-Tschebyscheff Array
Solves: Minimum beamwidth for a prescribed max. sidelobe level

25. Chapter 4
Antennas and Propagation Slide 25
Tschebyscheff Array
Array factor
Even number of antennas (M is twice # antennas)
Cosine Power Series

26. Chapter 4
Antennas and Propagation Slide 26
Tschebyscheff Array (2)
Tschebyscheff Polynomials
Recursion
Direct Computation with cos/cosh

27. Chapter 4
Antennas and Propagation Slide 27
Tschebyscheff Array (3)
Tschebyscheff Polynomials

28. Chapter 4
Antennas and Propagation Slide 28
Tschebyscheff Example
M = 3 (6 antenna elements)

29. Chapter 4
Antennas and Propagation Slide 29
Tschebyscheff Example (2)
OK, but
How do we map z to x?

30. Chapter 4
Antennas and Propagation Slide 30
Tschebyscheff Example (3)
Main beam at
x = 1 x = cos u
z = z0
Let z = z0 x

31. Chapter 4
Antennas and Propagation Slide 31
Tschebyscheff Example (4)
Straightforward generalization for higher orders.

32. Chapter 4
Antennas and Propagation Slide 32
Tschebyscheff Array (Generalized)

33. Chapter 4
Antennas and Propagation Slide 33
Gen. Tschebyscheff Array (2)
Can find the am using the same recursive procedure as before.

34. Chapter 4
Antennas and Propagation Slide 34
Comparison of Beamforming Methods
Δ=π/4, N=8, R0=10 (-20dB side lobes)

35. Chapter 4
Antennas and Propagation Slide 35
Summary
Antenna Arrays
Offer flexibility over single antenna elements
Array factor / Element Factor
Direct synthesis methods for designing AF
Beamforming
Considered mainly ULA
Uniform excitation (change phases)
Non-uniform: Binomial array, Tschebyscheff
Other possibilities
Non-ULA: circular array, rectangular, sparse arrays
Non-symmetric excitation
Non-linear processing