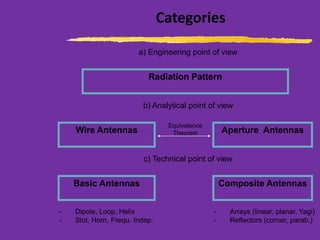
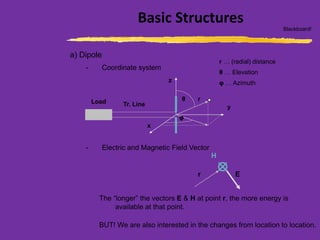
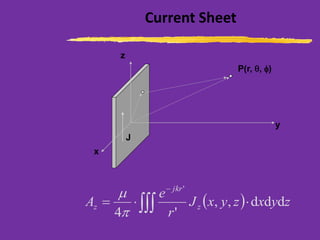
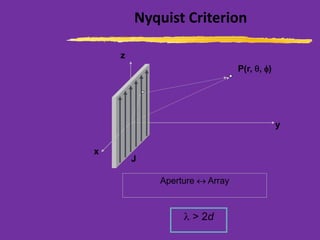
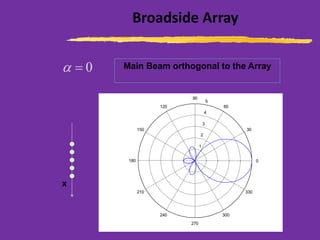
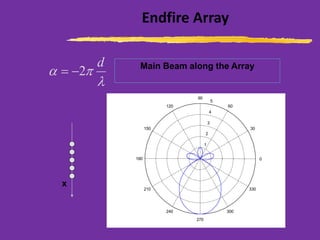
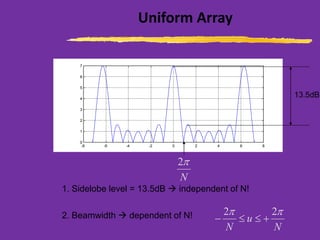
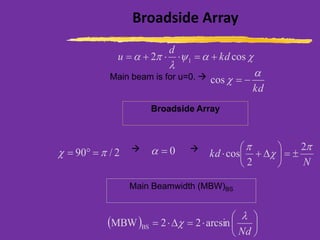
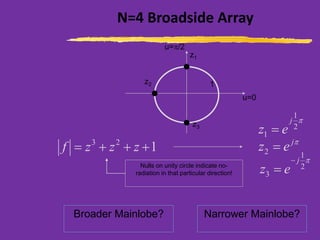
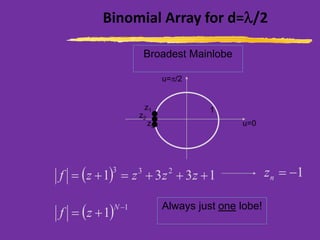
This document discusses wire antennas and antenna arrays. It begins by categorizing radiation patterns from an engineering, analytical, and technical perspective. It then covers basic wire antenna structures like dipoles and loops. The document focuses on linear, planar and array types including properties like radiation patterns, array factors, and design considerations for arrays like element spacing, progressive phase shifts and different array geometries. Specific array examples covered include uniform, broadside, endfire, binomial and filled disk arrays.