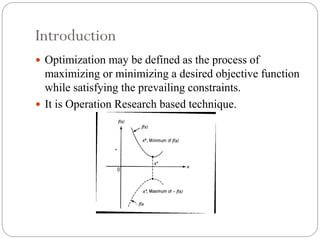
The document discusses the principles of optimization in engineering design, focusing on maximizing or minimizing objective functions while adhering to constraints. It explains different optimization techniques, including mathematical programming, stochastic processes, and statistical methods, and highlights software tools used in optimization such as ANSYS and CATIA. Additionally, it presents a practical example of optimization in a bracket design, which led to a significant reduction in weight and cost.

1. Presented By Guided By
GoreA. S. Prof. Rodge M.K.
2010MME007
M.Tech. CAD/CAM
CAD Based Optimization
Department of Production
Engineering, SGGSIE&T, Nanded

2. Introduction
 Optimization may be defined as the process of
maximizing or minimizing a desired objective function
while satisfying the prevailing constraints.
 It is Operation Research based technique.

3. Statement of a Optimization Problem:
 An optimization problem can be stated as follows:
Minimizes f(X)
subject to the constraints
gj (X)≤0, j=1,2,…….,m and lj (X)=0 , j=1,2,……...,p
 To find X={𝑥1 𝑥2 𝑥3... 𝑥n}T
where,
X is an n-dimensional vector i.e. the design vector
f(X) is termed the objective function
gj (X) and lj(X) are known as inequality and equality constraints
n number of variables
m and /or p number of constraints

4. Objectives:
 In the conventional design procedures there will be
more than one acceptable design, the purpose of
optimization is to choose the best one of the many
acceptable designs available.
 Example minimization of weight in aircraft and
aerospace structural design problems.
 Minimization of cost In civil engineering structural
designs
 Maximization of mechanical efficiency in mechanical
engineering systems design.

5. Commonly used OptimizationTechniques
1. Mathematical ProgrammingTechniques : To find the
minimum of a function of several variables under a
prescribed set of constraints, e.g. sequential quadratic
programming (SQP)
2. Stochastic ProcessTechniques : To analyze problems
described by a set of random variables with known
probability distribution , e.g. queuing theory
3. StatisticalTechniques : To build empirical models from
experimental data through analysis, e.g. Design of
Experiments

6. Optimization based on Finite Elements
 Used for dynamic response, heat transfer, fluid flow,
deformation and stresses in a structure subjected to loads
and boundary conditions.
Classification :
a. Parameter or size optimization : The objective function is
typically weight of the structure and the constraints
reflecting limits on stress and displacement.
b. Shape optimization : deals with determining the outline of
a body, shape and/or size of a hole, etc. The main concept
is mesh parameterization
c. Topology optimization : distribution of material, creation
of holes, ribs or stiffeners, creation/deletion of elements,
etc.

7. Role of Optimization

8. Softwares used:
 ANSYS
 IDEAS
 CATIA
 Unigraphics NX
 TOSCA

9. Optimization Methods in ANSYS
 Subproblem Approximation:-
o It is an advanced zero-order method.
o Requires only the values of the dependent variables, and
not their derivatives.
o It converts problem to an unconstrained optimization
problem because minimization techniques for the latter
are more efficient.
o The conversion is done by adding penalties to the
objective function.

10. Optimization Methods in ANSYS
 First Order:-
o It is based on design sensitivities, for high accuracy.
o It converts the problem to an unconstrained one by
adding penalty functions to the objective function.
o finite element representation is minimized and not an
approximation.
o Both methods series of analysis-evaluation-modification
cycles.

11. ElementType
 PLANE82:-
o Higher order version of the 2-D, four-node element
o For mixed (quadrilateral-triangular) automatic meshes
Assumptions
o The area of the element must be positive.
o The element must lie in a global X-Y plane

12. Example:- Bracket

13.  Problem Formulation:-
o Minimize,
Volume = f(R1;R2;R3;R4;W) [10 mm3]
o Subject to,
0 ≤VM ≤ 349:33 [1 MPa]
25≤ R1 ≤ 45 [1 mm]
15 ≤ R2 ≤ 45 [1 mm]
5 ≤ R3 ≤ 45 [1 mm]
5 ≤ R4 ≤ 45 [1 mm]
5 ≤W ≤ 170 [1 mm]

14. Iterations
 Set 1:-
o V max- 344.58MPa
o Vol- 16199 mm3
 Set 2:-
o V max -283.73 MPa
o Vol-12956 mm3

15.  Set 3:-
o V max-345.78 MPa
o Vol-8907.4 mm3
 Set 4:-
o V max-349.65 MPa
o Vol-8843.8 mm3

16.  Set 5:-
o V max-350.77 MPa
o Vol-8829.1 mm3

17. Results
 DesignVariables R1,R2,R3,R4,W

18.  Volume

19.  Von Mises Stresses

20. Application of Bracket

21. Conclusion
 The First order method is good method for optimization
 The optimization helps reduce 45.4% of the structure weight
 As material reduced then obviously cost is also reduced

22. References
 CAD Based Optimization by Celso Barcelos, Director of
Development MacNeal-Schwendler Corporation2003
 Multiphysics CAD-Based Design Optimization A. Vaidya, S.
Yang and J. St. Ville
 D. Spath, W. Neithardt and C. Bangert, “Integration of Topology
and Shape Optimization in the Design Process”, International
CIRP Design Seminar, Stockholm, June 2001.
 CAD-based Evolutionary Design Optimization with CATIA V5
Oliver KÄonig, Marc Winter mantel
 Structural optimization using ANSYS classic and radial basis
function based response surface models by Vijay Krishna
THE UNIVERSITY OFTEXAS AT ARLINGTON MAY 2009
 J.P. Leiva, and B.C. Watson, “Shape Optimization in the Genesis
Program”, Optimization in Industry II, Banff, Canada, Jun 6-100,
1999.

23. Thank You