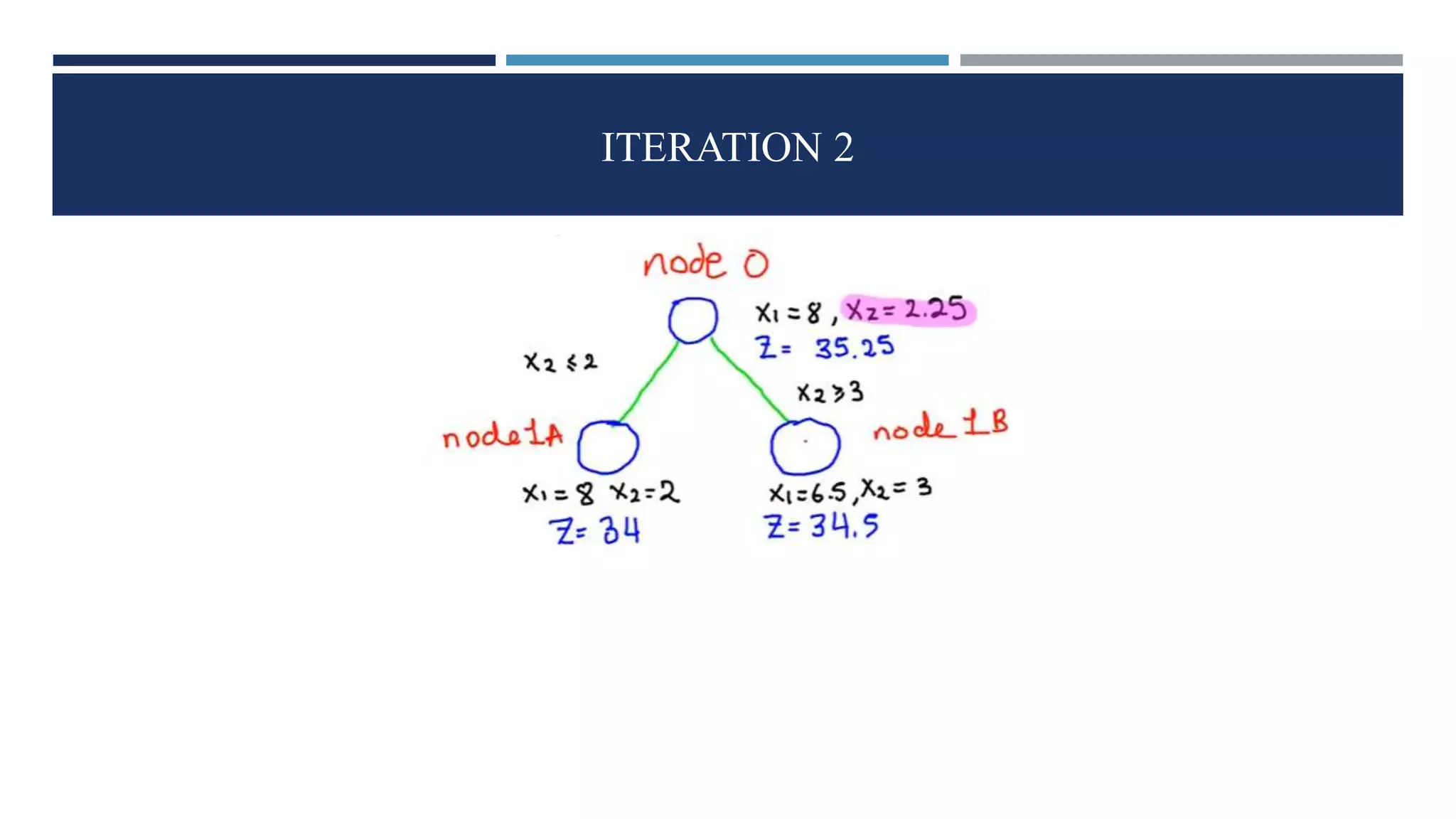
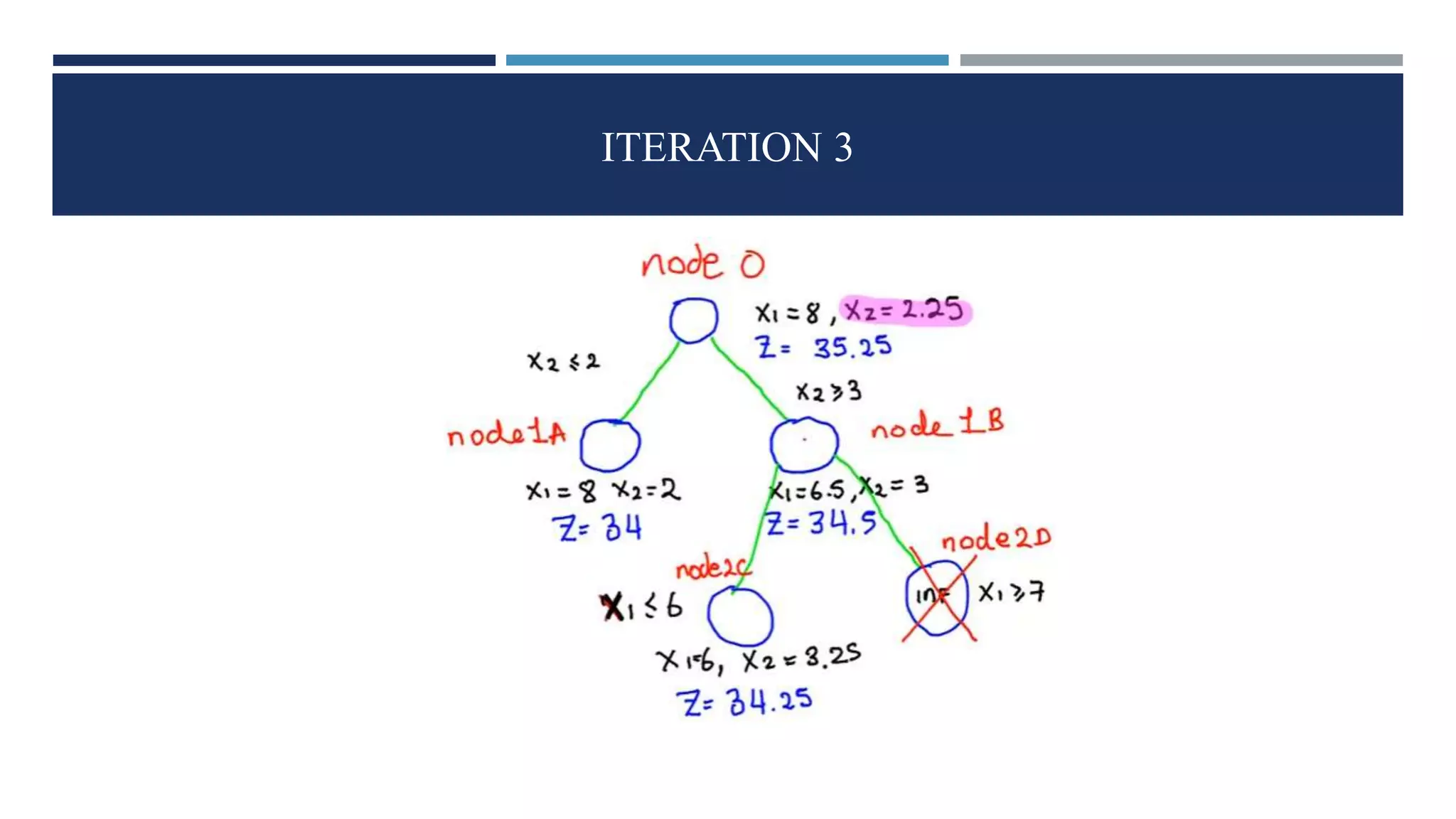
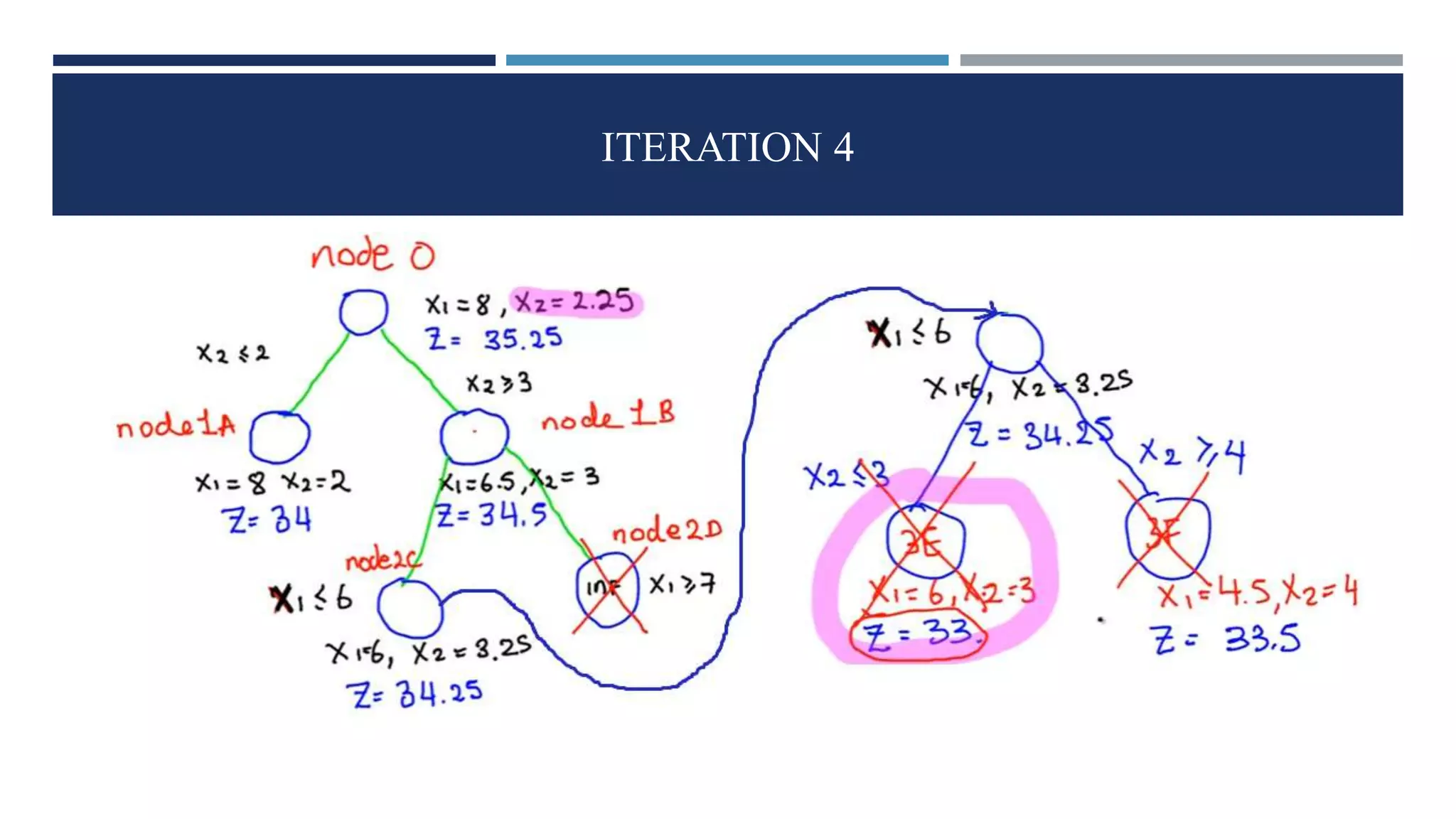
The document discusses integer linear programming (ILP) and its classification as a NP-hard problem, focusing on the branch and bound technique as a solution method. This involves dividing the problem into smaller sub-problems and estimating their solutions to find optimal outcomes. Examples of problems that can be formulated as ILPs are also provided, showcasing the practical application of these concepts.

1. BRANCH AND BOUND TECHNIQUE TO
SOLVE INTEGER LINEAR PROGRAMMING
GROUP MEMBERS
AYAM AJMERA – 1401096
KAIVALYA SHAH – 1401108
RATNESH SHAH – 1401110

2. INTEGER PROGRAMMING AND INTEGER LINEAR PROGRAMMING
 Integer programming (IP) is a mathematical optimization program in which some of the variables or
sometimes all the variables are restricted to be integers.
 Integer Linear programming (ILP) is a special case of IP where the objective function and constraints are
linear.
 Integer programming is considered as a NP-Hard problem.
 A special case of 0-1 integer linear programming, is included in one the Karp’s 21 NP-complete problems.
 Standard form of ILP is as follows
maximize 𝑐 𝑇
𝑥
subject to 𝐴𝑥 + 𝑠 = 𝑏
𝑠 ≥ 0
and 𝑥 𝜖 𝑍 𝑛

3. INTEGER LINEAR PROGRAMMING
 There are 2 variants of integer linear programming
 Mixed Integer Linear Programming – some variables are constrained to be integers,
while others can be non-integers.
 Zero-One Linear Programming – variables are bounded to be either 0 or 1 i.e., binary.
 Some problems that can be formulated as ILP’s are as follows
 Travelling salesman problem
 Vertex cover and other covering problems
 Set packing and other packing problems
 Boolean Satisfiability

4. BRANCH AND BOUND ALGORITHM
 Branch and bound is an algorithm design paradigm for discrete and combinatorial
optimization problems, as well as general real valued problems.
 A branch-and-bound algorithm consists of forming a rooted tree where the root is the full set of
candidate solution and the leaves are the set of candidate solutions (or subset of solution set).
 Before enumerating the candidate solutions of a branch, the branch is checked against upper and
lower bounds on the optimal solution, and is discarded if it cannot produce a better solution than
the best one found so far by the algorithm.
 The method was firstly proposed by A. H. Land and A. G. Doig in 1960 for discrete
programming.
 It is the most commonly used tool for solving NP-hard optimization problems.

5. BRANCH AND BOUND TECHNIQUE TO SOLVE ILP
 This is a type of divide and conquer method.
 The original problem is divided into multiple smaller problems (branching of a
problem). This is the dividing part of the method.
 The conquering part is done by estimating how good a solution, we can get from these
smaller problems.
 For this task, we may have to divide the small problem further, until we get a problem
which we can handle efficiently.
 So, the part where the original problem is divided into smaller parts is called branching
and the part where we try to estimate the goodness of the solution is called bounding.

6. LINEAR PROGRAMMING RELAXATION
 For an integer programming model P, the linear programming model we get by dropping the
requirements that all the variables must be integers is called Linear Programming Relaxation.
 The steps are:
 Divide a problem into different sub-problems.
 Calculate the LP relaxation of a sub-problem
 The LP problem has no feasible solution.
 The LP problem has an optimal integer solution. Compare this optimal solution with the best solution we
know.
 The LP problem has an optimal solution that is worse than the incumbent.
In all the cases above, we know all we need to know about that sub-problem. We say that sub-problem is
fathomed.
 The LP problem has an optimal solution that are not all integers, better than incumbent. In this case, we
would have to divide this sub-problem further and repeat.

7. EXAMPLE
Maximize 3x1 + 5x2
Subject to
2x1 + 4x2 < 25
x1 < 8
2x2 < 10
xi > 0, xi’s are integers

8. ITERATION 1

9. ITERATION 2

10. ITERATION 3

11. ITERATION 4

12.  We can see that the solution of the objective function
obtained from node 3F is 33.5 which is less than the
solution obtained from the objective function from node
1A which is 34.
 So, we cannot further branch from node 3F.
 The final answer is obtained from node 1A which is,
x1 = 8, x2 = 2, and z = 34

13. THANK YOU