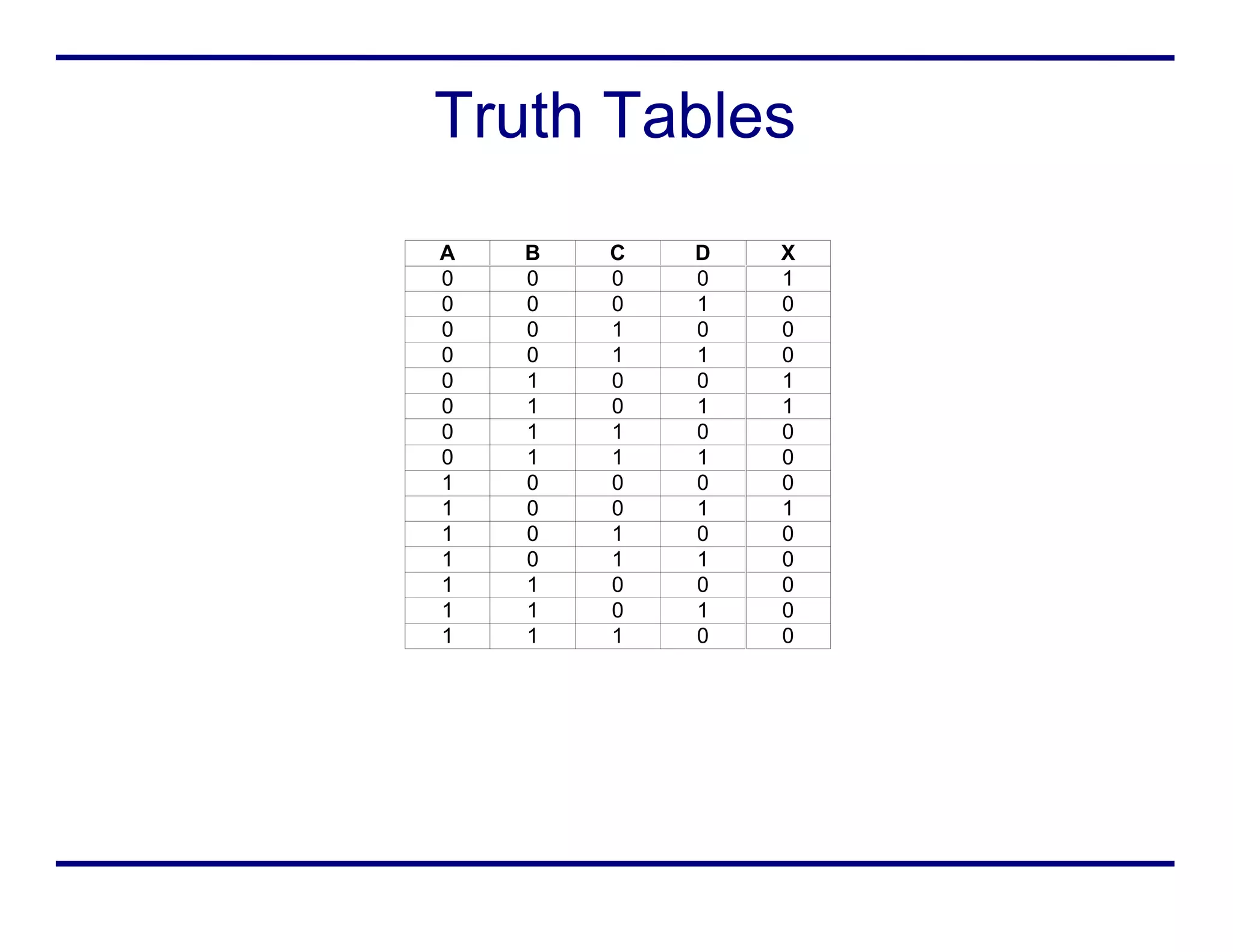
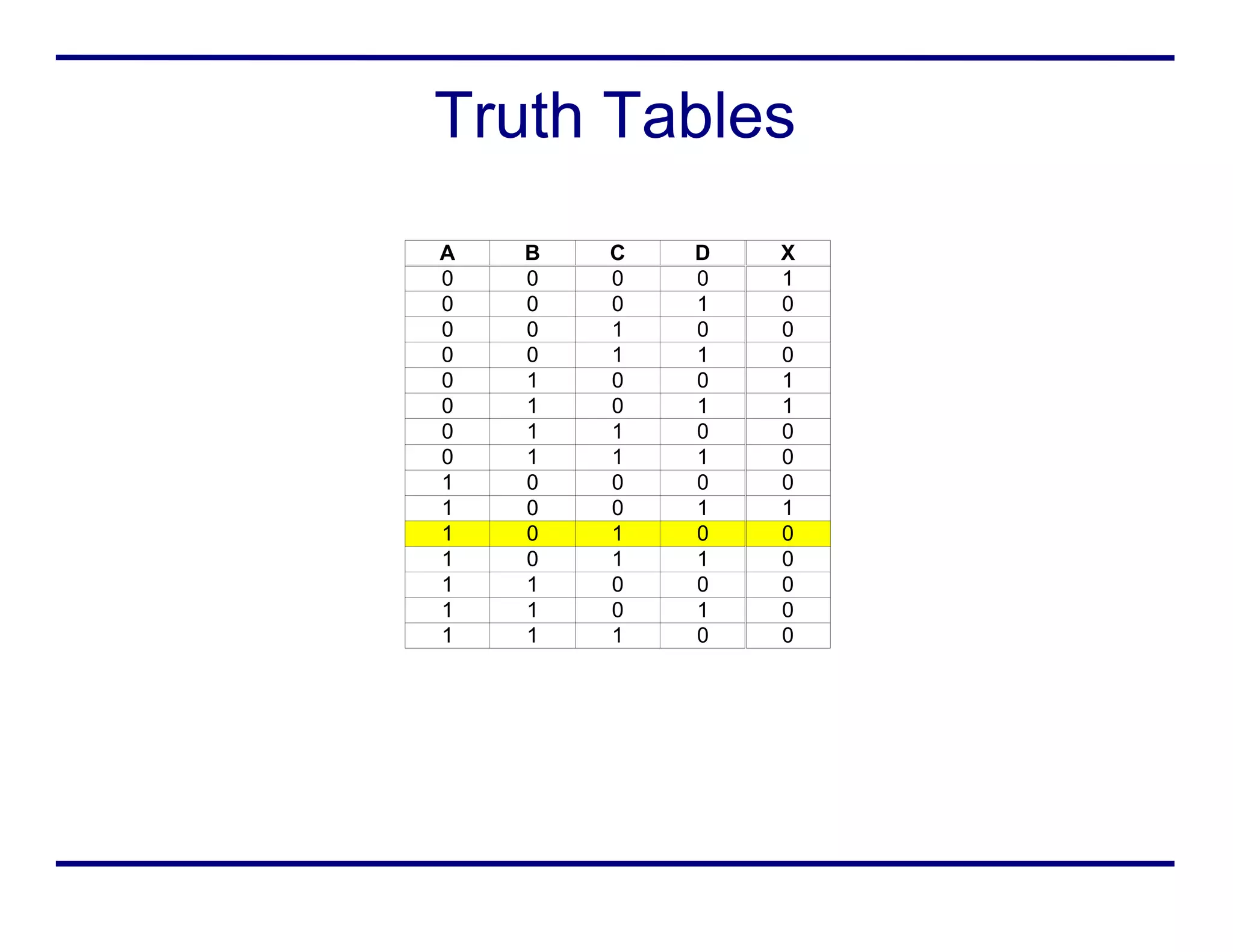
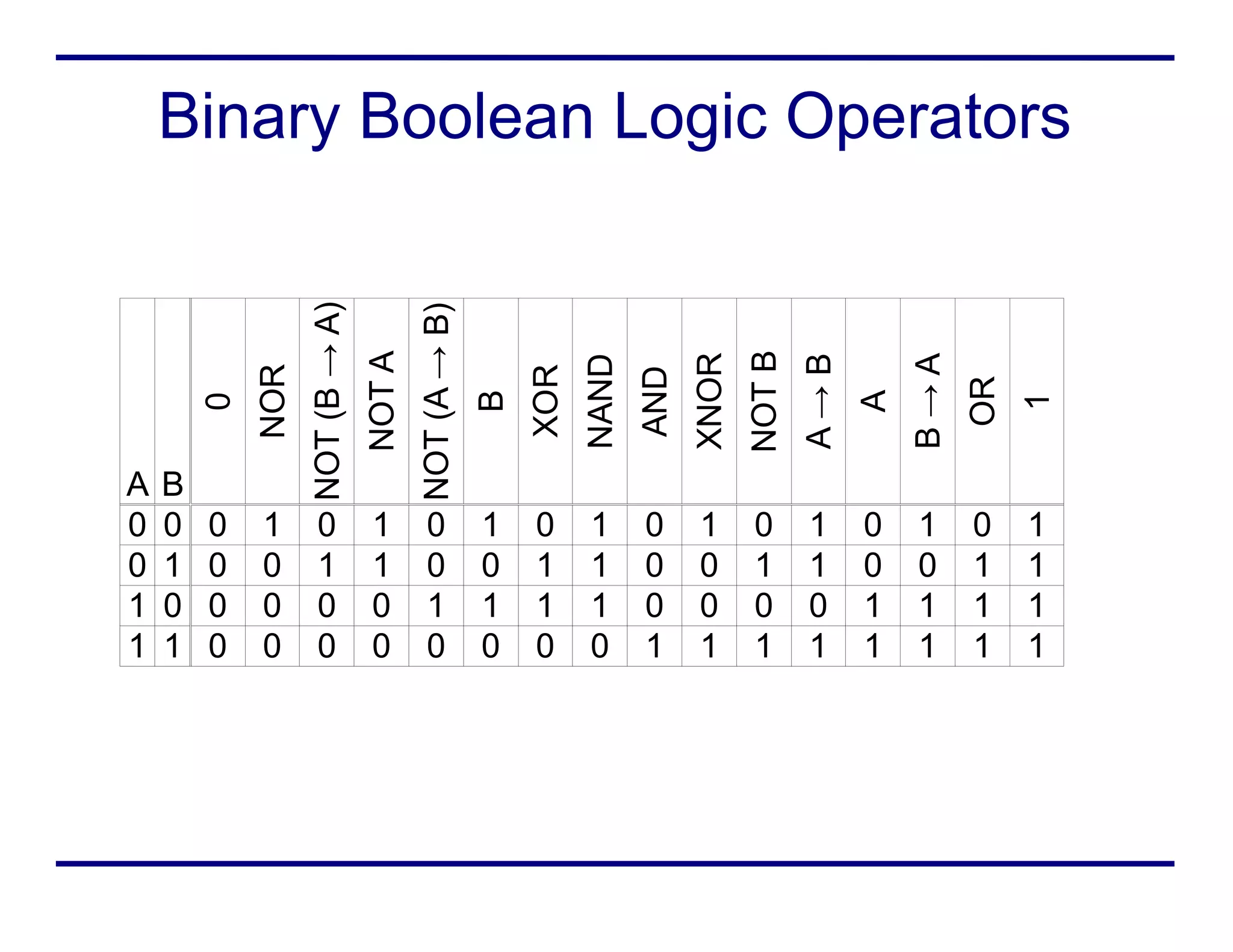
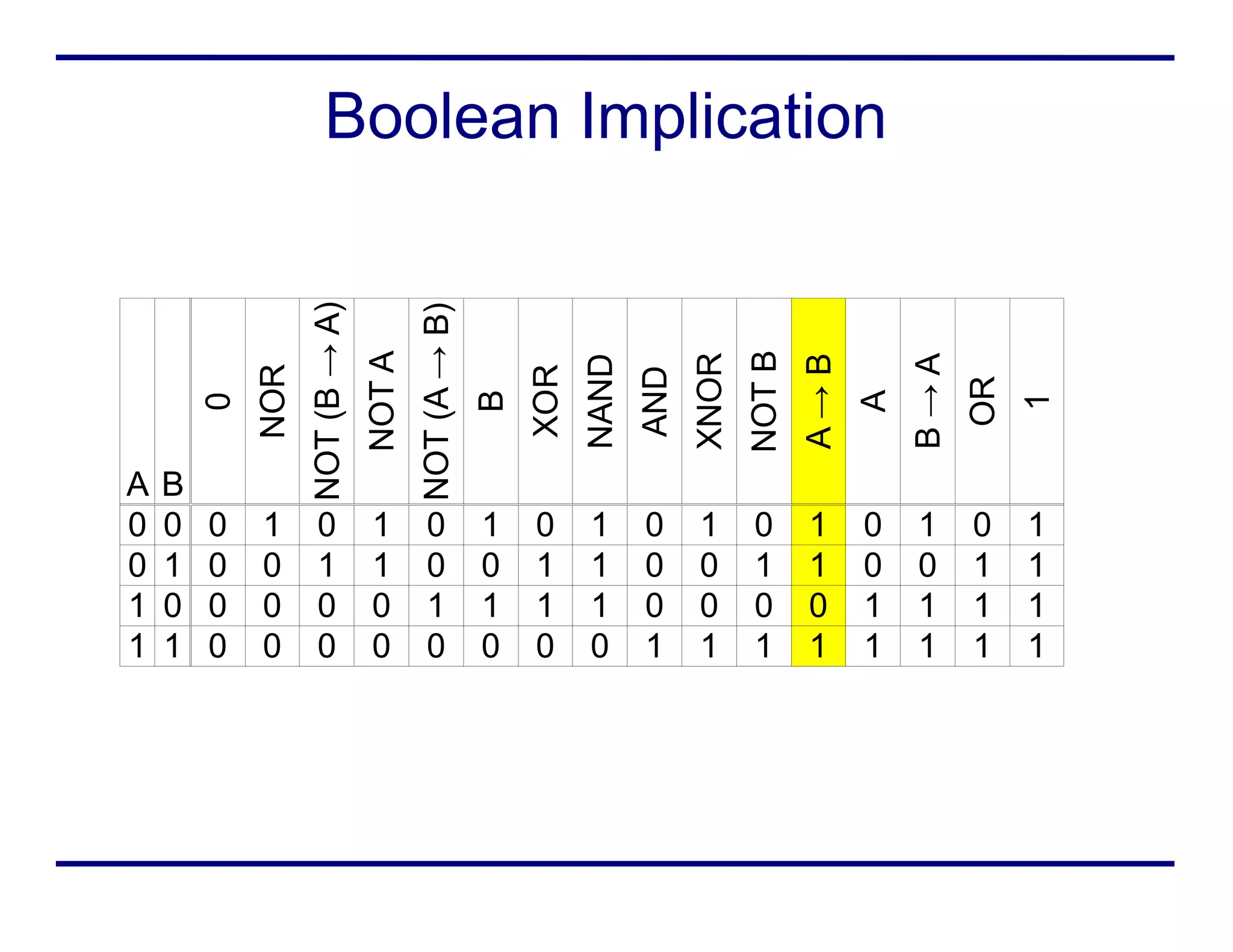
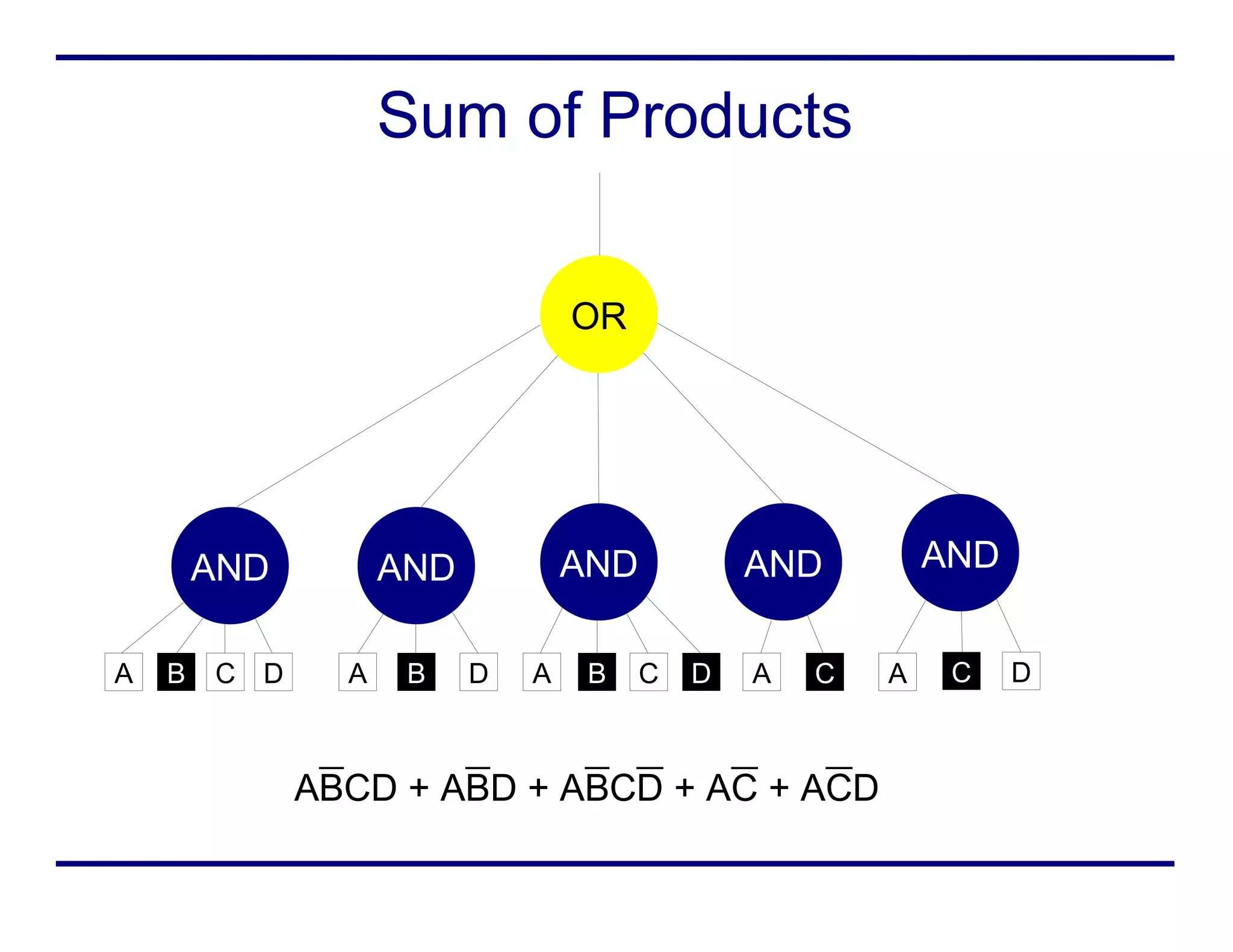
Boolean logic represents true and false values using 1s and 0s. It uses various operators like AND, OR, NOT to combine boolean variables. Truth tables define the output for every possible combination of input variables. Boolean expressions can be written in sum of products form or minterm form. Boolean logic is used in digital circuits, computer science, and mathematics.

1. Boolean Logic

2. Representing Boolean Values
Domain Values
Mathematics True False
Computer Science 1 0
Electronics
On Off
Vcc Ground

3. Boolean Logic Notation
Mathematical
Formal
Typed A’B’CD + AB’CD
Java/C !A&&!B&&C&&D||A&&!B&&C&&D
¬A ¬ᴧ BᴧCᴧD ᴠA ¬ᴧ BᴧCᴧD
A.B.C.D + A.B.C.D

4. Truth Tables
A B C D X
0 0 0 0 1
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 1
0 1 0 1 1
0 1 1 0 0
0 1 1 1 0
1 0 0 0 0
1 0 0 1 1
1 0 1 0 0
1 0 1 1 0
1 1 0 0 0
1 1 0 1 0
1 1 1 0 0

5. Truth Tables
A B C D X
0 0 0 0 1
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 1
0 1 0 1 1
0 1 1 0 0
0 1 1 1 0
1 0 0 0 0
1 0 0 1 1
1 0 1 0 0
1 0 1 1 0
1 1 0 0 0
1 1 0 1 0
1 1 1 0 0

6. Binary Boolean Logic Operators
A B
0
NOR
NOTA
B
XOR
NAND
AND
XNOR
NOTB
A
OR
1
0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
NOT(B→A)
NOT(A→B)
A→B
B→A

7. Boolean Implication
A B
0
NOR
NOTA
B
XOR
NAND
AND
XNOR
NOTB
A
OR
1
0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
NOT(B→A)
NOT(A→B)
A→B
B→A

8. Sum of Products
ANDANDANDANDAND
OR
BADCB DCBAD ACAA DC
ABCD + ABD + ABCD + AC + ACD

9. Minterm Form
A B C D X Y
0 0 0 0 1 1
0 0 0 1 0 1
0 0 1 0 0 1
0 0 1 1 0 0
0 1 0 0 1 1
0 1 0 1 1 0
0 1 1 0 0 1
0 1 1 1 0 1
1 0 0 0 0 0
1 0 0 1 1 1
1 0 1 0 0 0
1 0 1 1 0 1
1 1 0 0 0 1
1 1 0 1 0 0
1 1 1 0 0 0
1 1 1 1 0 1
X = ABCD + ABCD + ABCD + ABCD
Y = ABCD + ABCD + ABCD + ABCD + ABCD
+ ABCD + ABCD + ABCD + ABCD + ABCD

10. Reduction
X = ABCD + ABC + ABCD
X = ABCD + ABC(D + D) + ABCD
X = ABCD + ABCD + ABCD + ABCD
X = ABCD + ABC.1 + ABCD

11. Mathematics
f:B0
×B1
…×Bn
→B
f:Bn
→B
f:Bn
→Bm
B = {true, false}

12. Conclusion