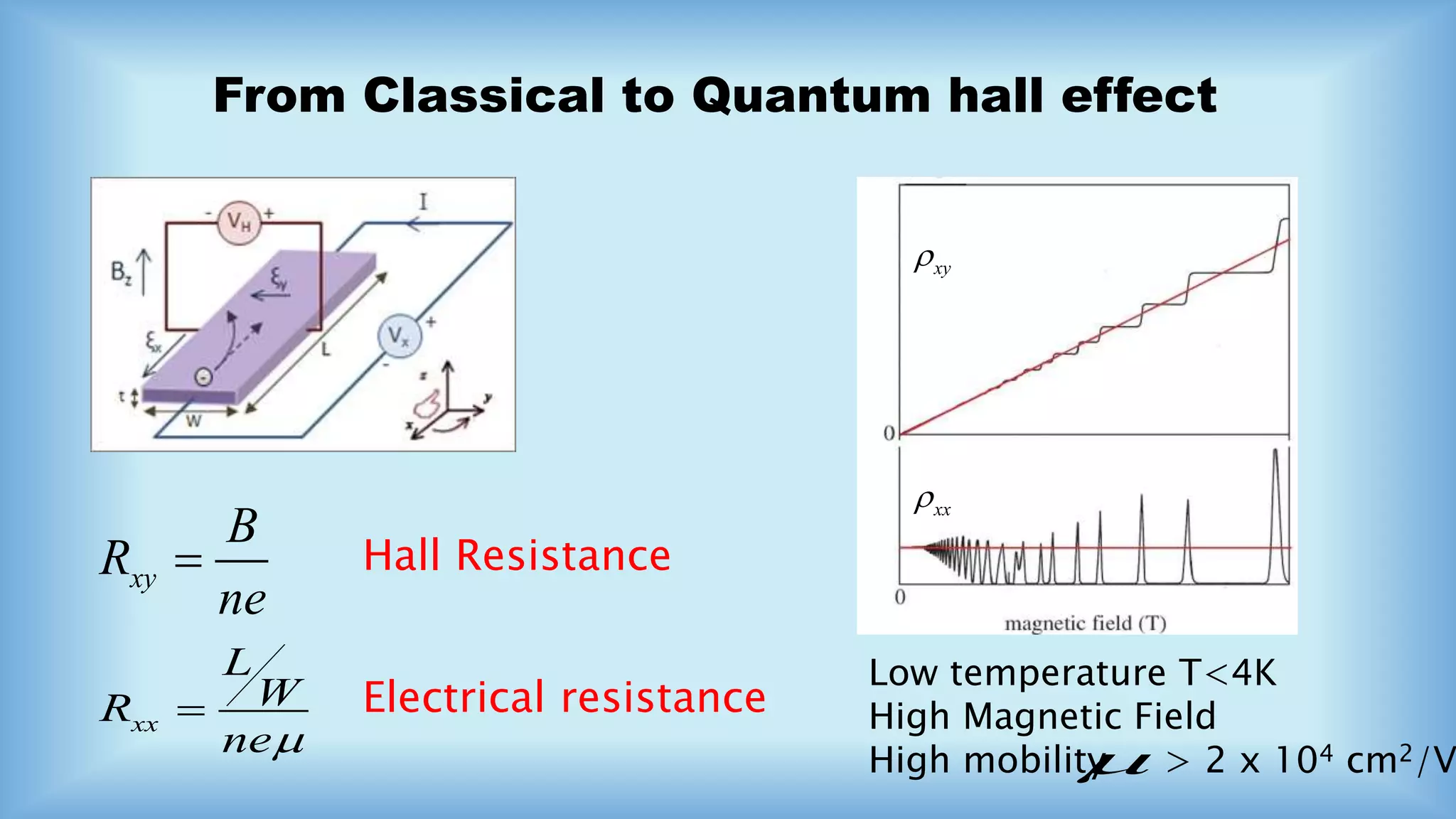
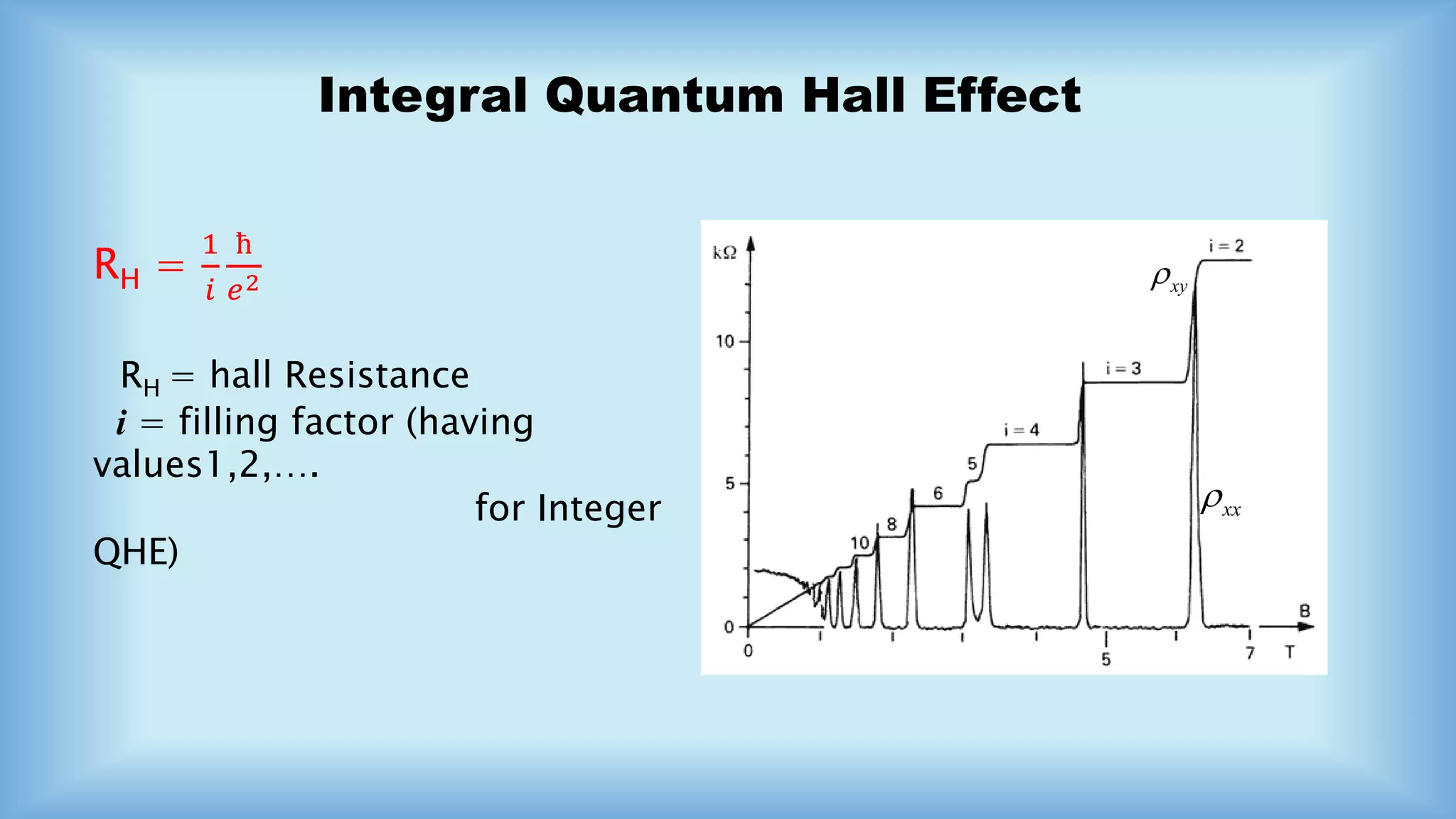
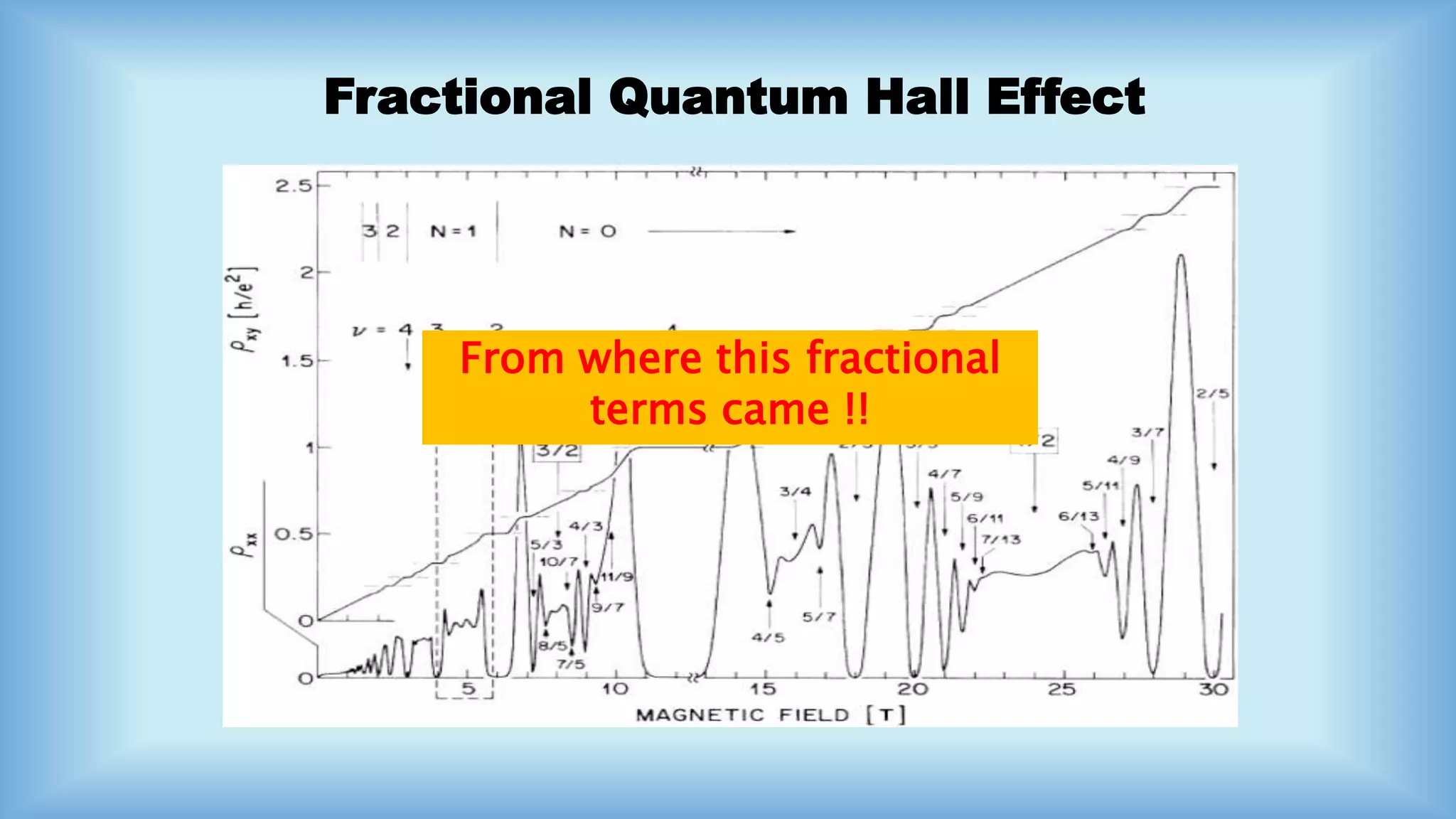
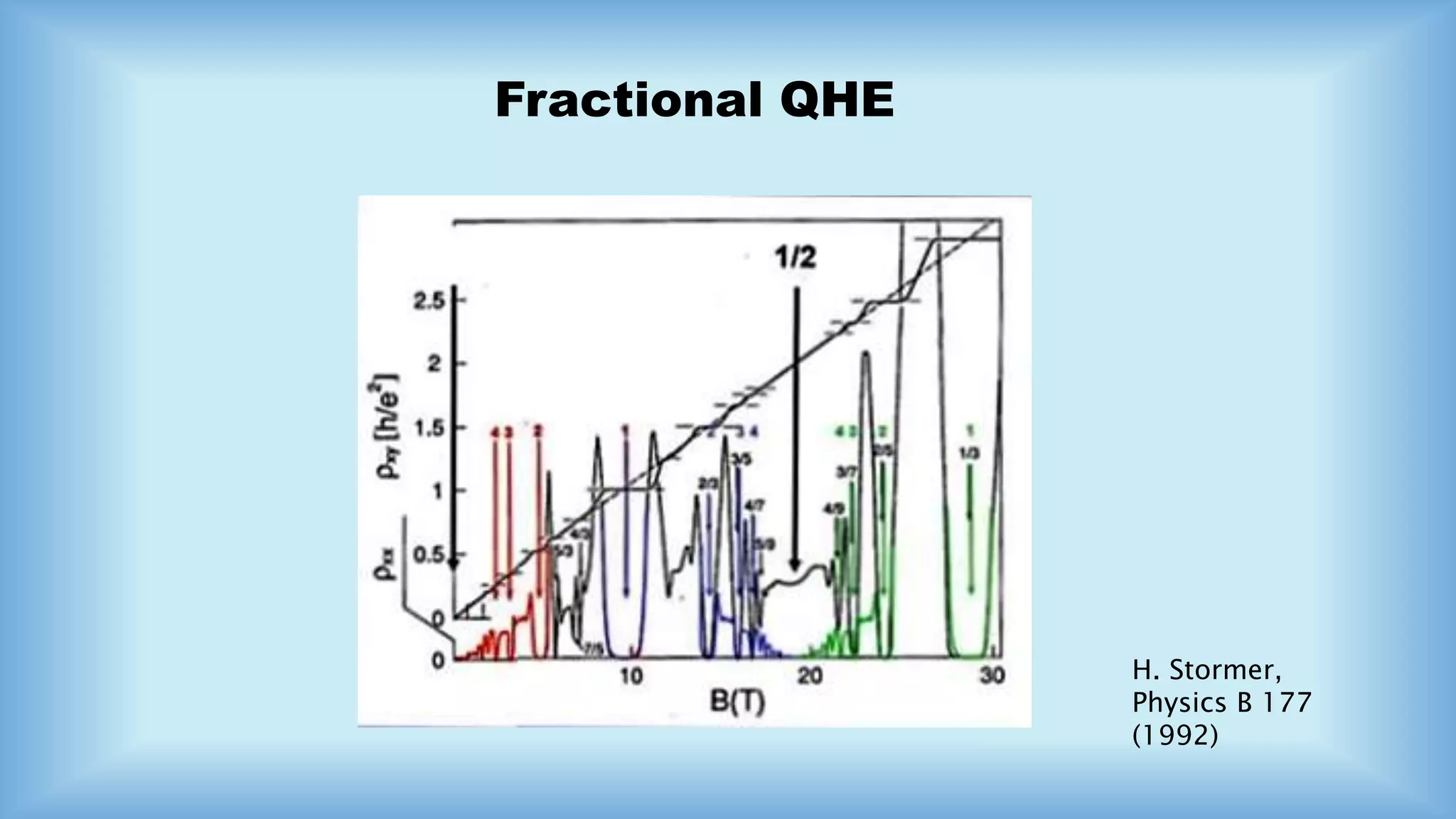
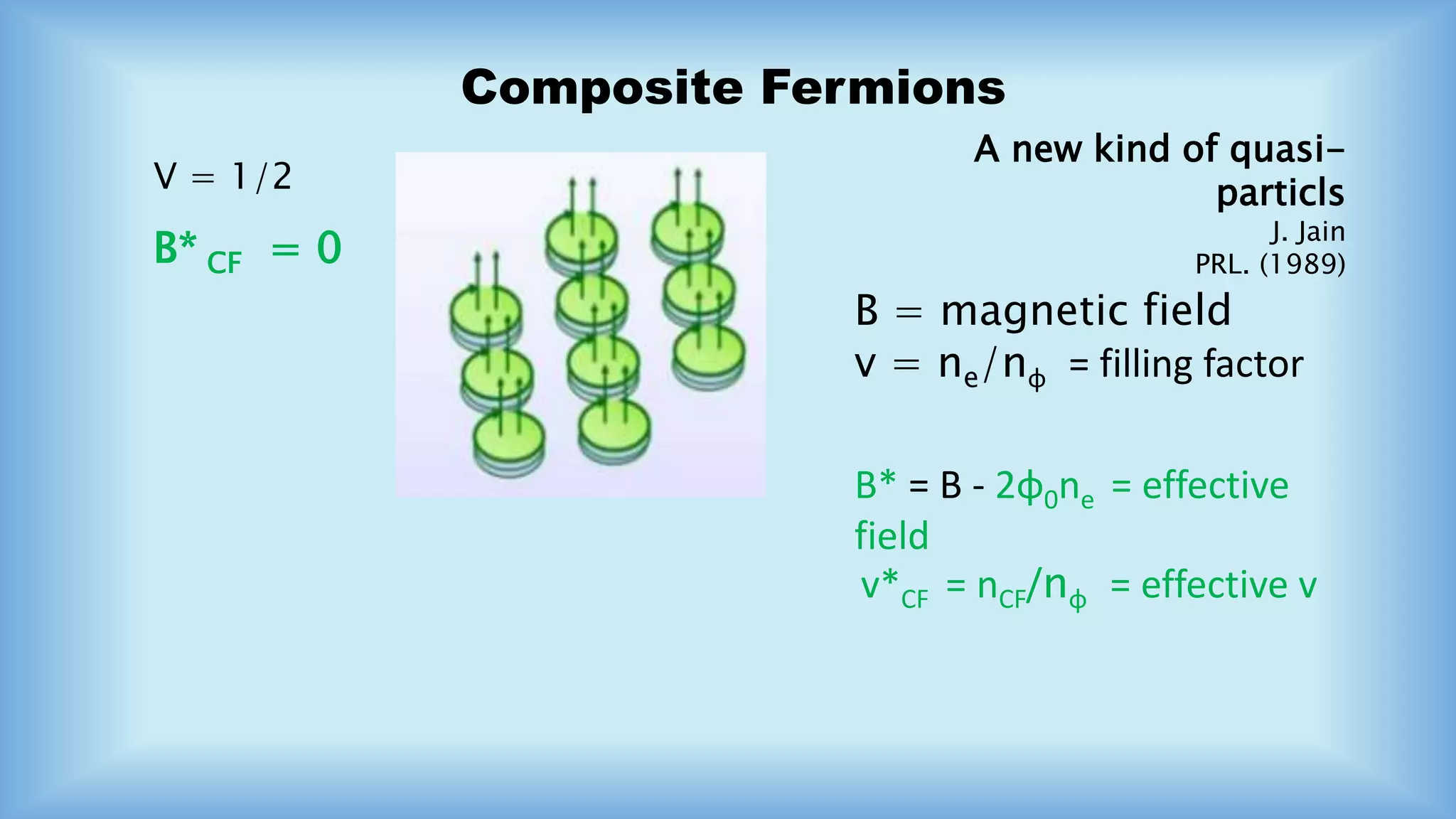
The document discusses the Integral and Fractional Quantum Hall Effect, detailing the transition from classical to quantum effects in a 2D electron gas under high magnetic fields. It highlights significant concepts like Hall resistance, the Nobel Prize awarded for discovering the quantized Hall effect, and the emergence of composite fermions in fractional quantum Hall states. The applications of this phenomenon are extensive, including its use in magnetometers, current sensors, and quantum resistance standards.

1. THE INTEGRAL &
FRACTIONAL QUANTUM
HALL EFFECT
SUDIPTO DAS
15PH40041
Presented by
IIT Kharagpur

2. Outline
Classical to quantum hall effect
2 Dimensional Electron gas (2DEG) in B-field
Integral Quantum Hall Effect
Fractional Quantum Hall Effect
Composite Fermion
Application

3. From Classical to Quantum hall effect
xx
L
WR
ne

xy
B
R
ne

Electrical resistance
Hall Resistance
xy
xx

4. Low temperature T<4K
High Magnetic Field
High mobility > 2 x 104 cm2/V
From Classical to Quantum hall effect
xy
xx
xx
L
WR
ne

xy
B
R
ne

Electrical resistance
Hall Resistance

5. 2DEG in quantizing B-field
 
2
*
1
2
H p eA
m
 
Landau Gauge, (0, )A xB
2
* *
( )
;
2 2
yx
y y
eBx kp
H p k
m m

  
h
h
2
* 2 2
* *
1
( )
2 2
;k c
x
c
p
H m x Bx
m
e
m
    yk
k eBx 
h
,
( 1/ 2)
( , ) ( ) y
n
ik y
n k n k
E n
x y xx e

 
 
 
h
xk centre
coordinate

6. xq= xk + (h/eBL)
Thus flux between neighbouring states, ɸ0 = B.{ (xq-
xk)L } = h/e Dirac flux
quanta
Degeneracy of States

7. Integral Quantum Hall Effect
The Nobel Prize in
Physics 1985
was awarded to Klaus
von Klitzing "for the
discovery of the
quantized Hall effect”

8. Integral Quantum Hall Effect
RH =
1
𝑖
ћ
𝑒2
RH = hall Resistance
i = filling factor (having
values1,2,….
for Integer
QHE)
xy
xx

9. Fractional Quantum Hall Effect
From where this fractional
terms came !!

10. Electrons in B-field
 Flux quantum:
ɸ0 = BA = Bπr2 =
h/e
Degeneracy:
nɸ = B/ɸ0 = eB/h
Filling factor:
v = ne/ nɸ

11. Fractional QHE
H. Stormer,
Physics B 177
(1992)

12. Flux Attachment Transformation
Fermionic:
𝛹(Z1, Z2) = - 𝛹(Z2, Z1) Fermionic
Antisymmetry
Bosonic:
𝛹(Z1, Z2) = - 𝛹(Z2, Z1)eiπ Fermionic
Antisymmetry
𝛹(Z1, Z2) = + 𝛹(Z2, Z1) +2π phase
shift

13. Composite Fermions
A new kind of quasi-
particls
J. Jain
PRL. (1989)
V = 1/2
B* CF = 0
B = magnetic field
v = ne/nɸ = filling factor
B* = B - 2ɸ0ne = effective
field
v*CF = nCF/nɸ = effective v

14. Composite Fermions
v =
1
v*CF =
1
v*CF = 2
v = 1/3 v*CF = p v =
𝑝
2𝑝+1
v = 2/3 v*CF = p v =
𝑝
2𝑝−1
q* CF= 2(e/3) + (-e) = - e/3 q*CF =
−𝑒
2𝑝+1
q* CF= 2(2e/3) + (-e) = + e/3 q*CF =
+𝑒
2𝑝−1
Charge of flux quantum
Ρbkgnd = +ene
q+ = A Ρbkgnd = +ene/nɸ = +ev

15. Fractional QHE

16. Applications
 Used as Magnetometers, i.e. to measure magnetic field.
 Hall effect sensor is also used as Current Sensor.
 Magnetic Position Sensing in Brushless DC Electric Motors
 Automotive fuel level indicator.
 Spacecraft propulsion.
 Quantum hall effect can be used for a determination of h/e2 or as a
resistance standard.
 Since the inverse fine structure constant α-1 is more or less identical h/e2 , high-
precision measurements of the quantized hall resistance are important for
all areas in physics that are connected with the fine structure constant.

17. THANK YOU