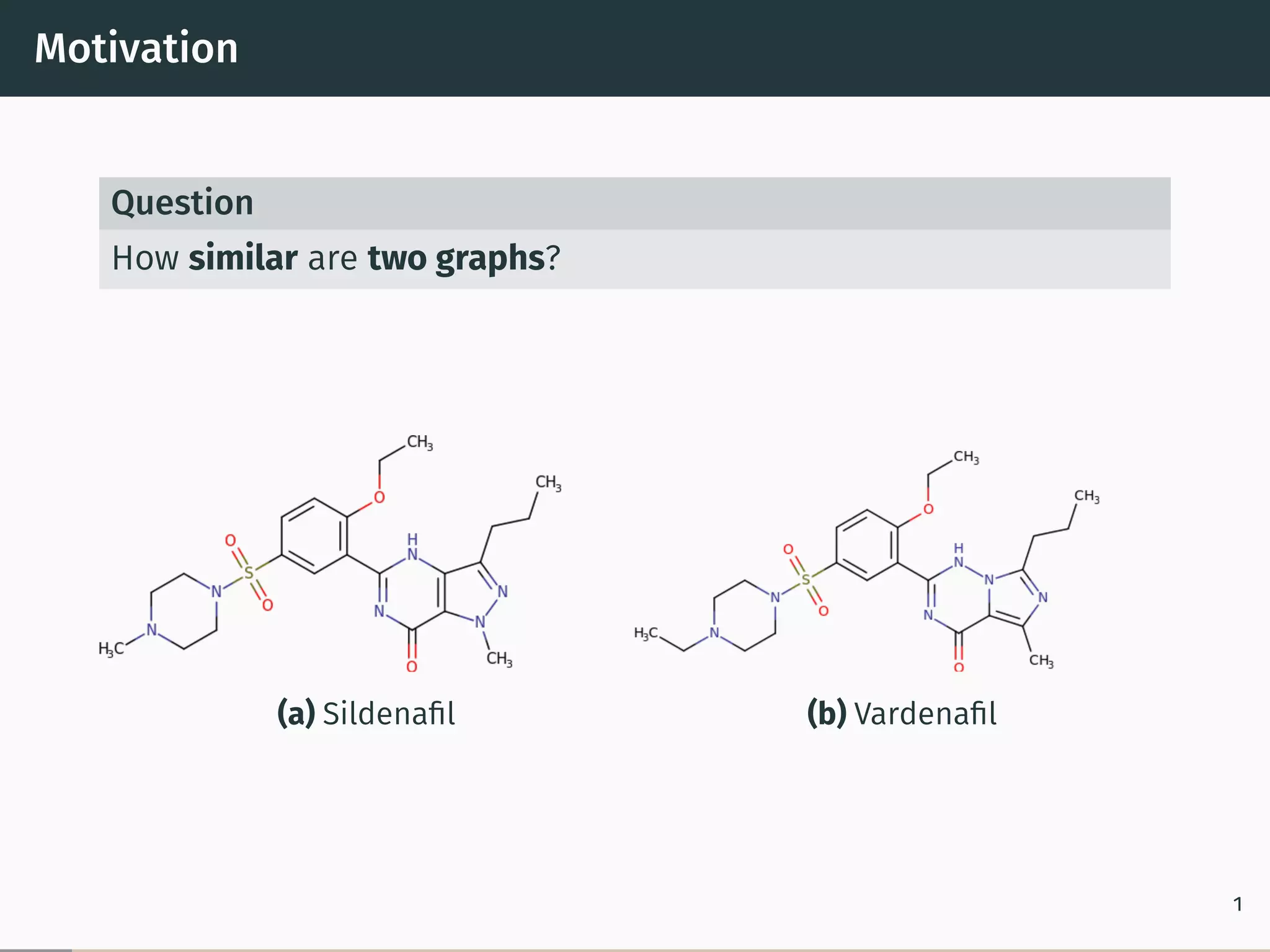
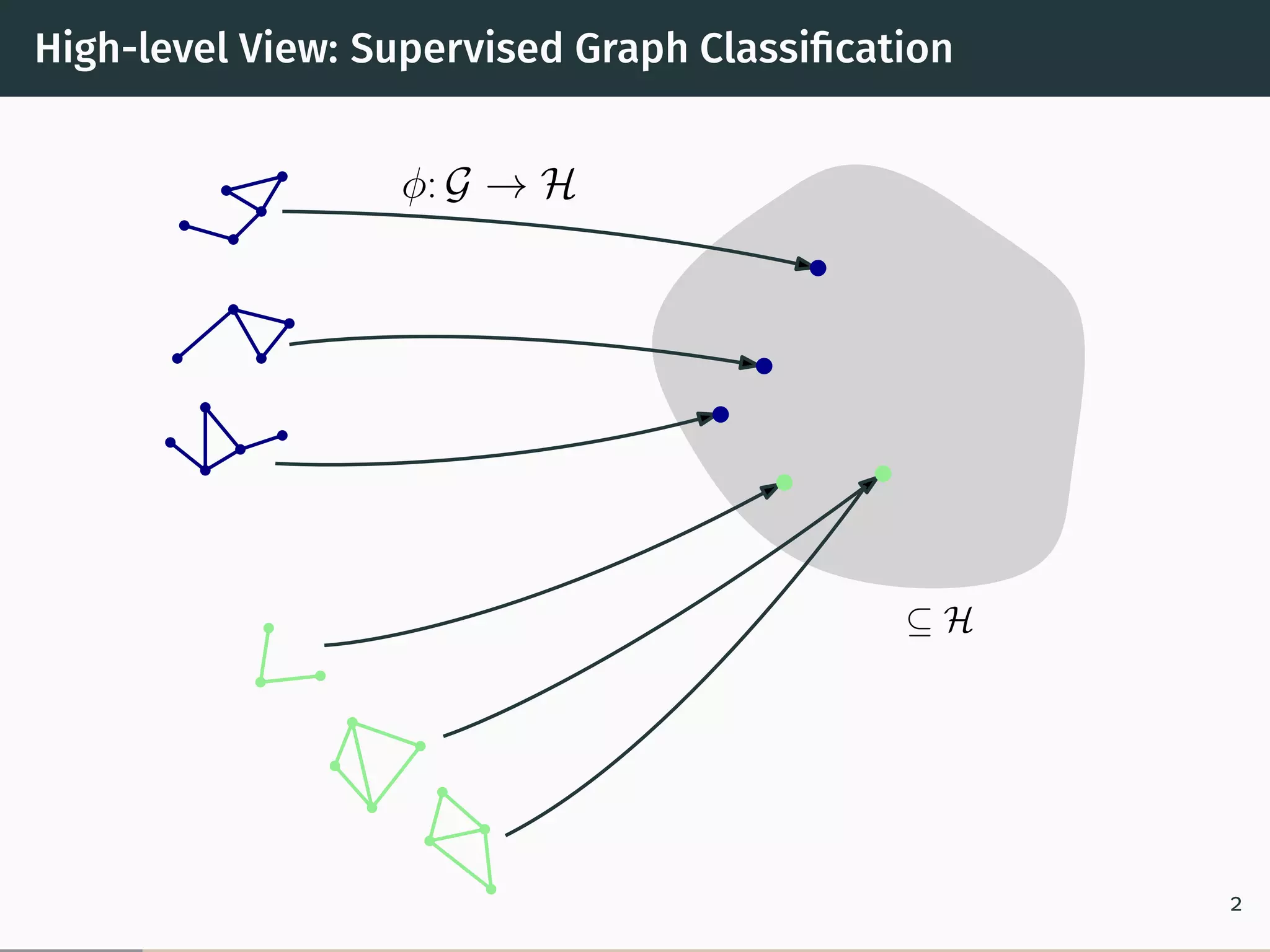
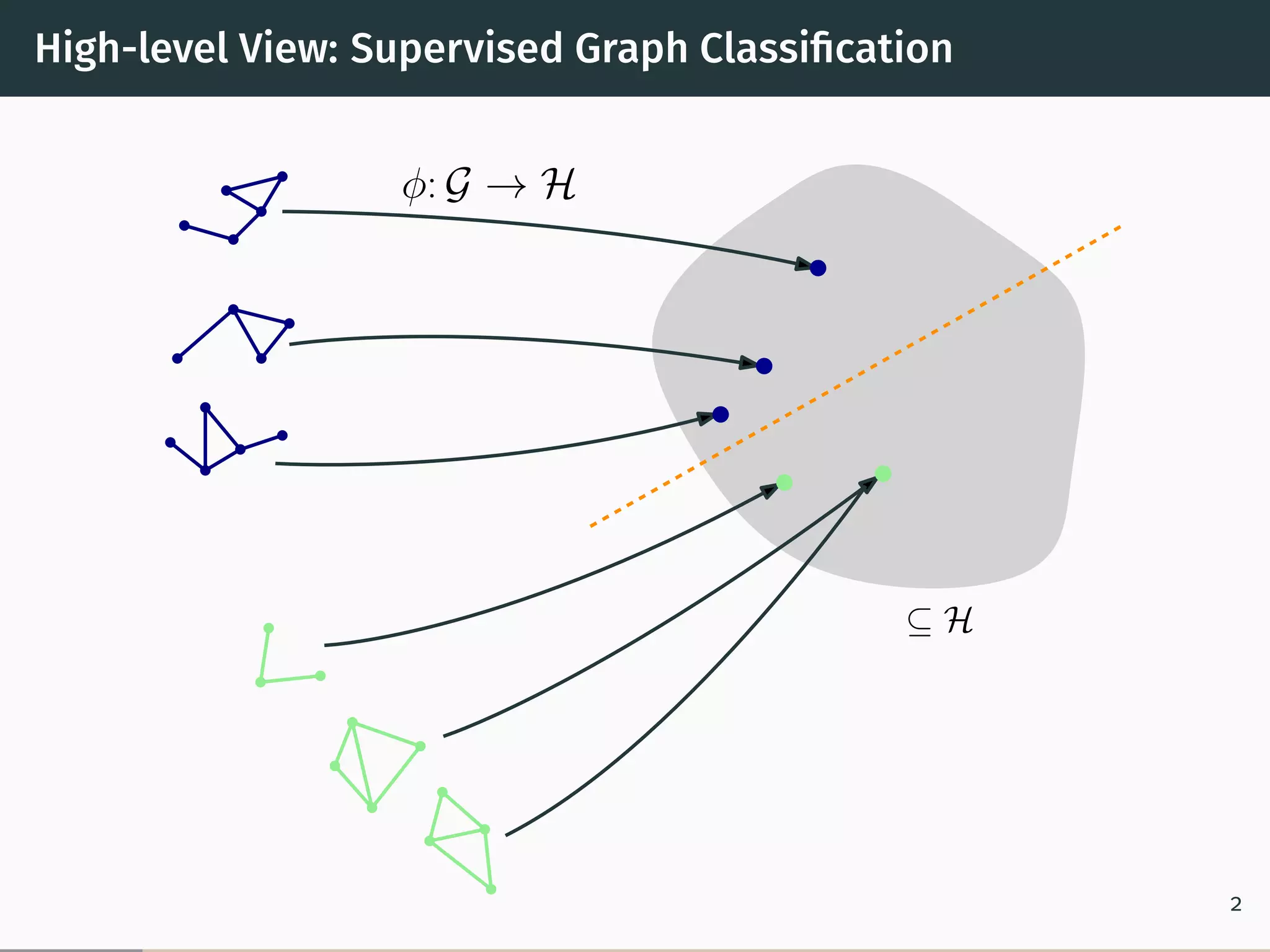
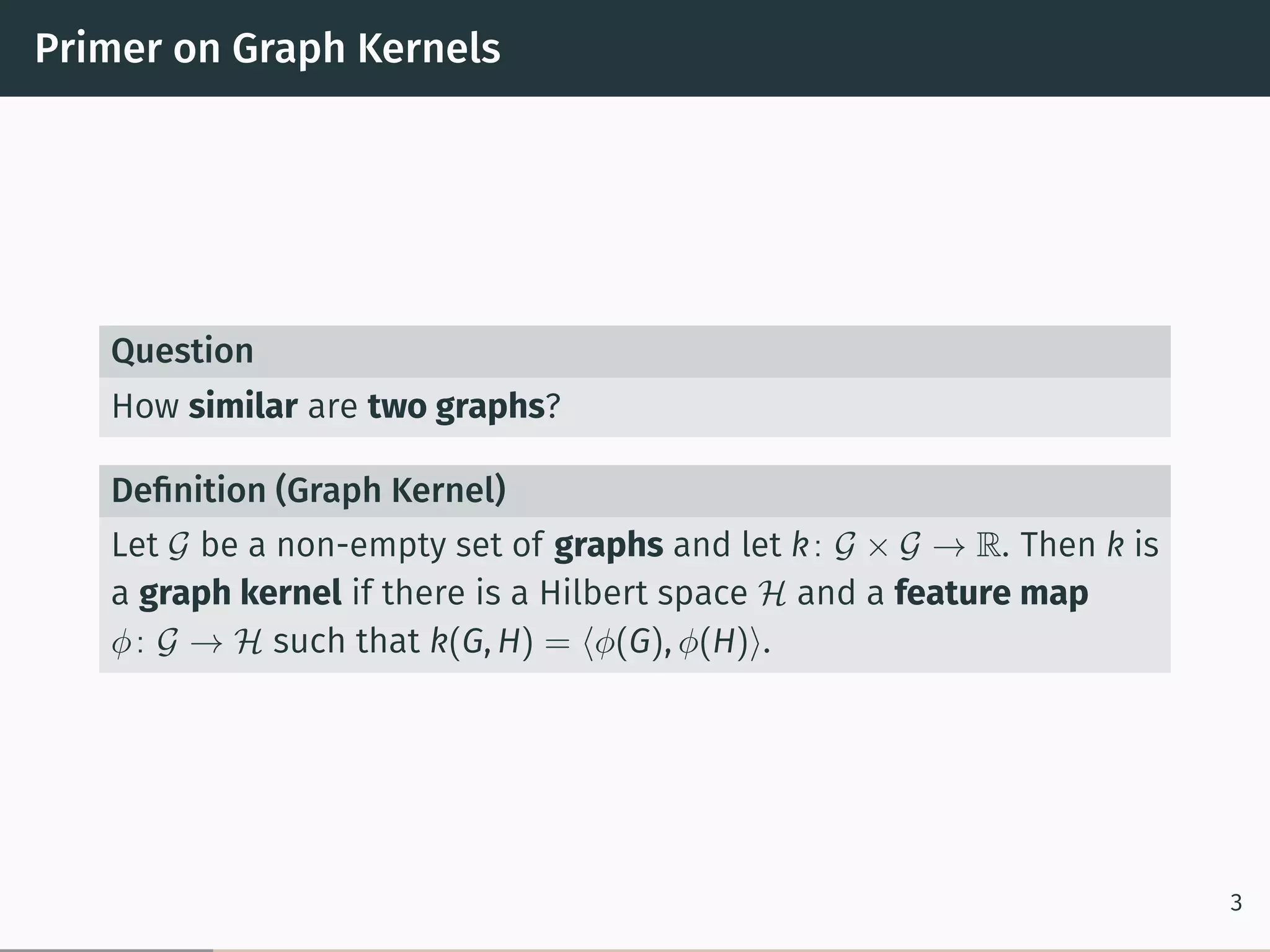
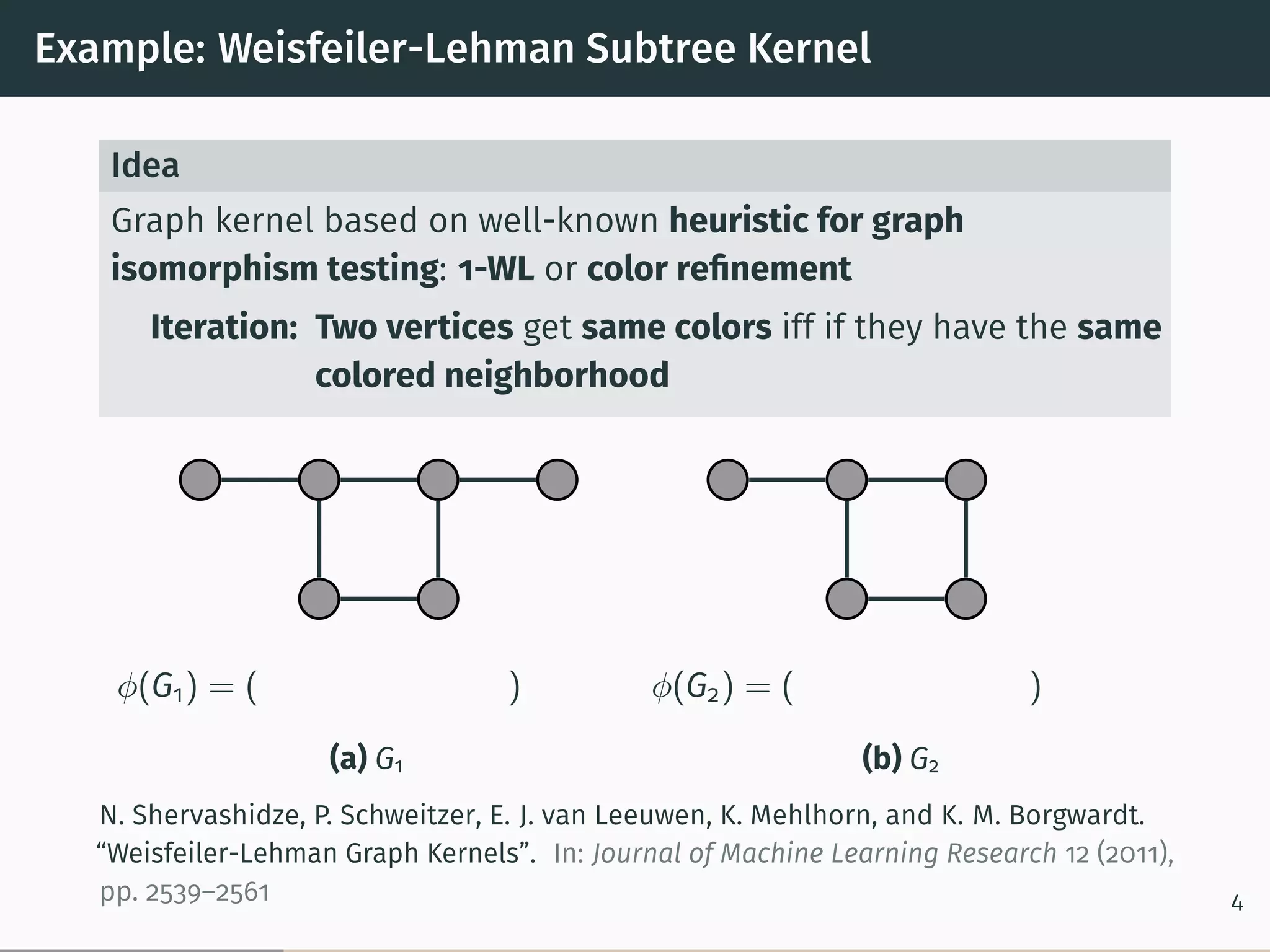
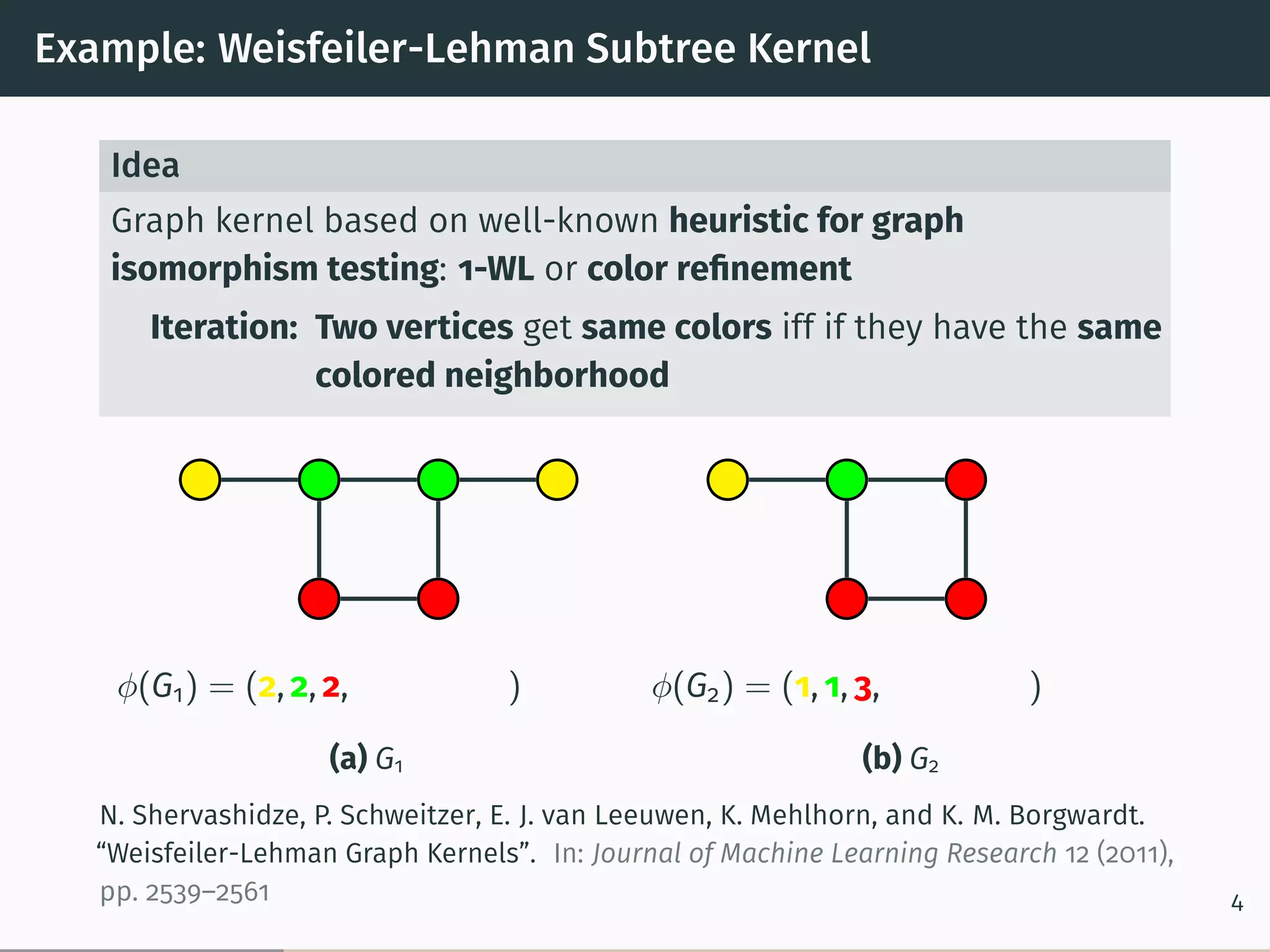
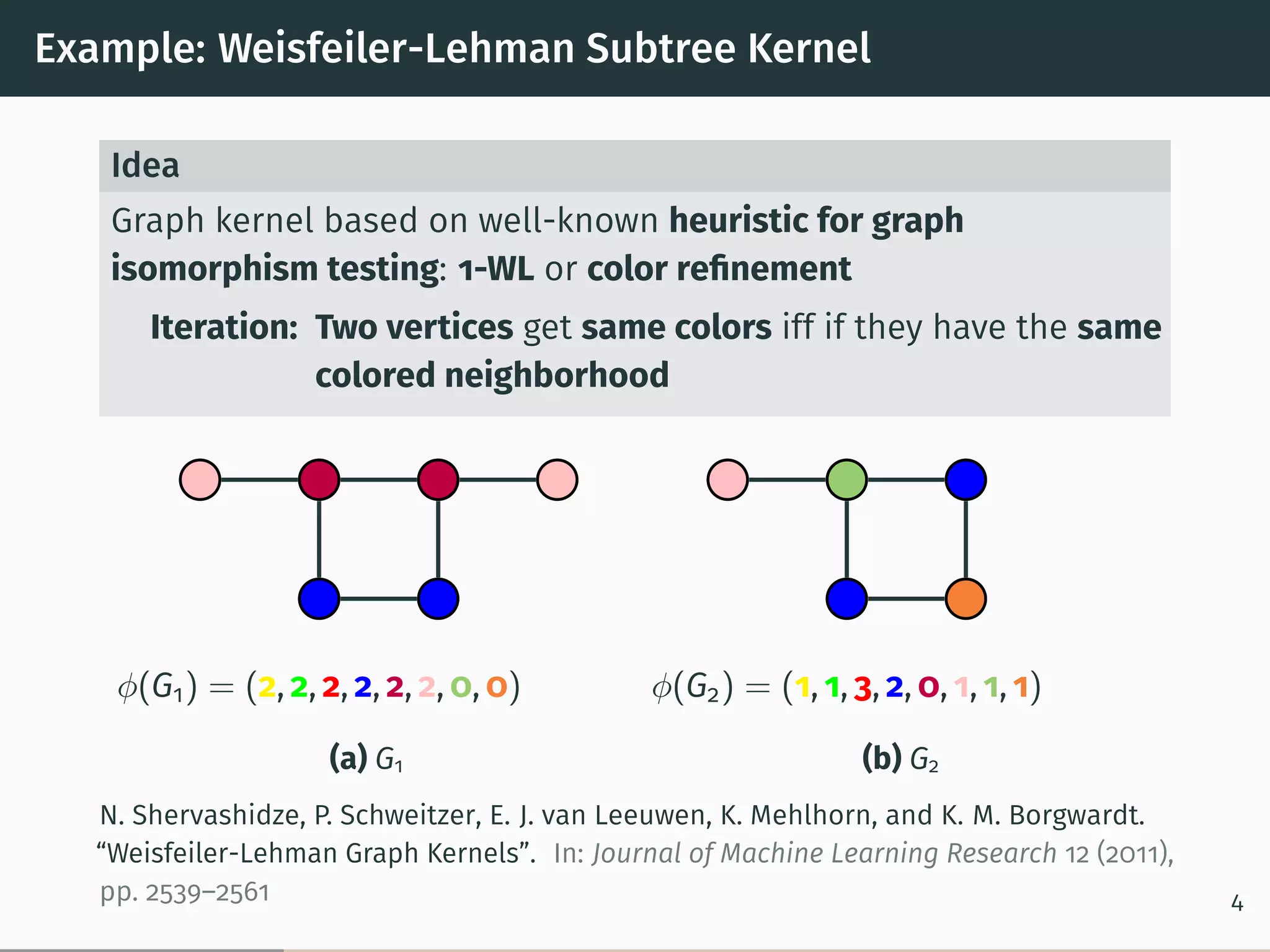
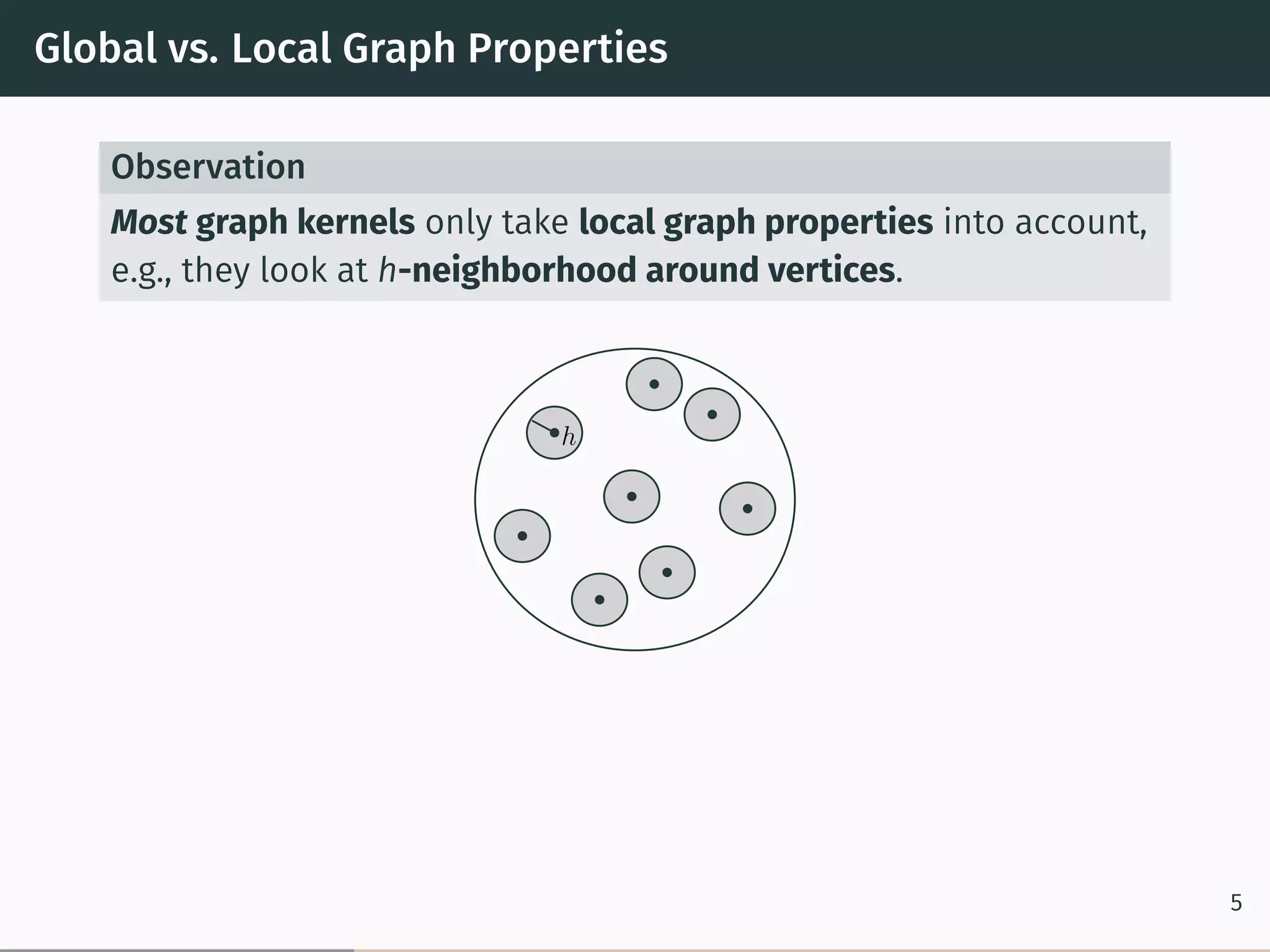
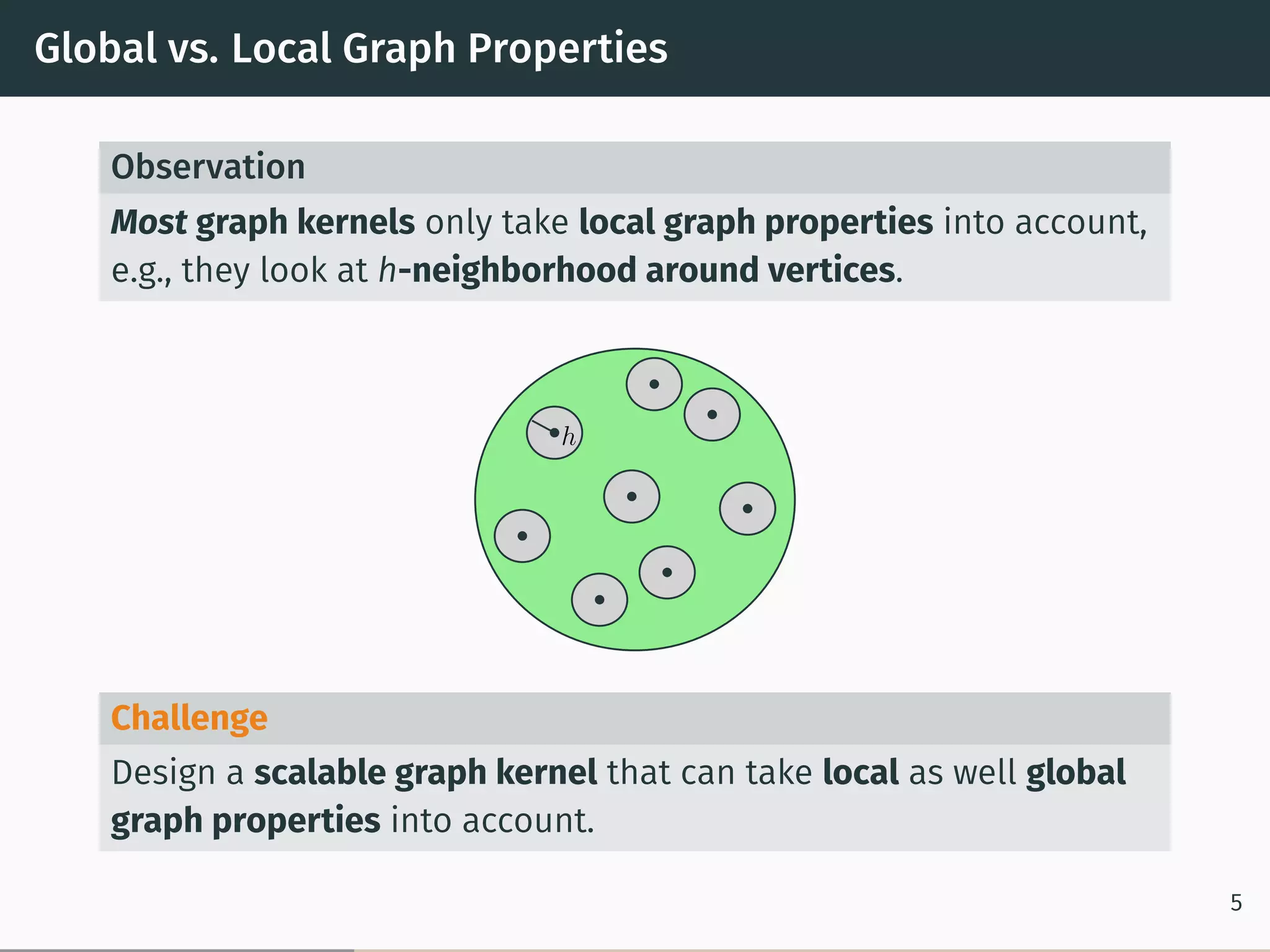
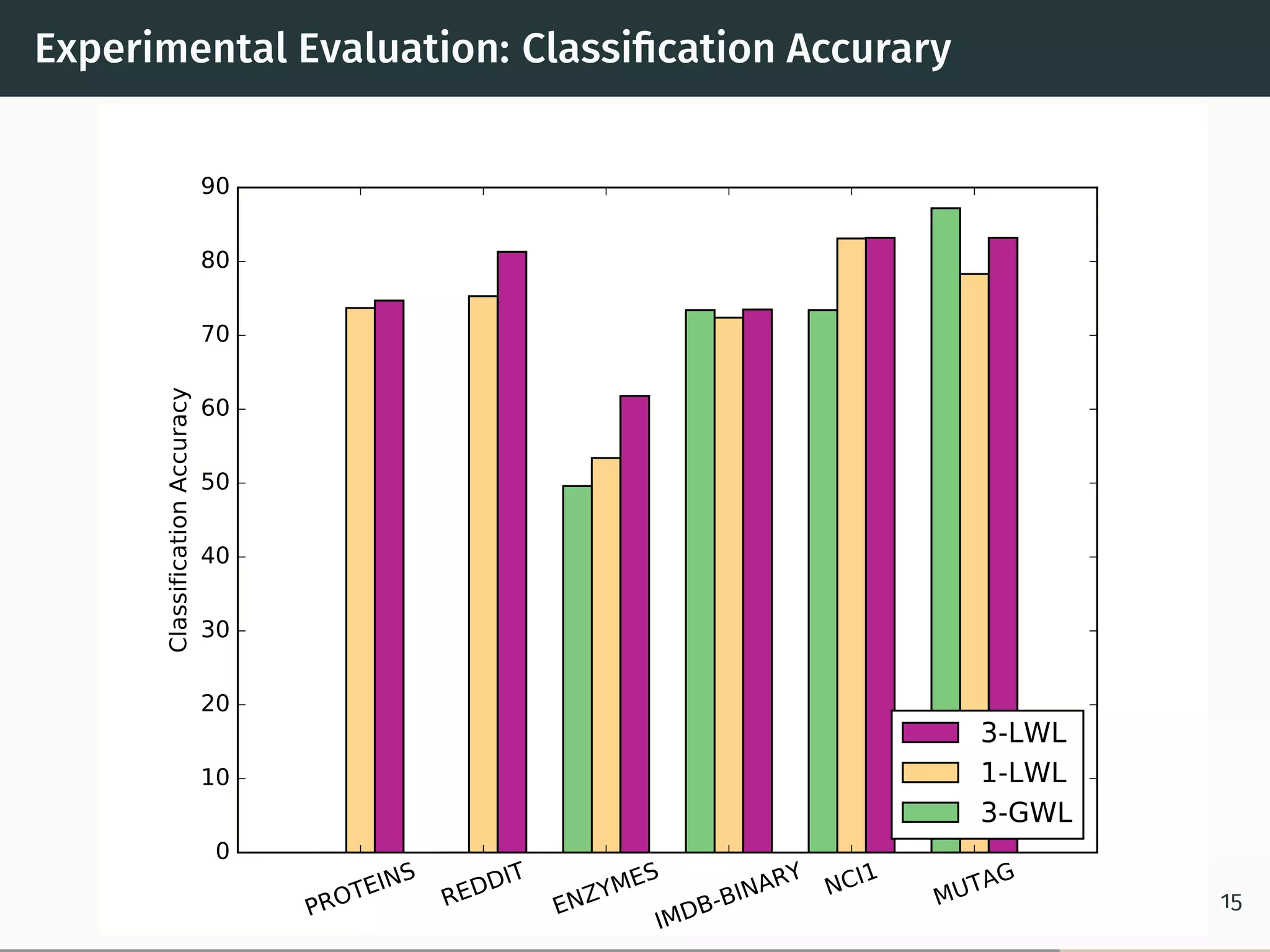
This document proposes a new graph kernel called the glocalized Weisfeiler-Lehman graph kernel. It extends the classic Weisfeiler-Lehman graph kernel to consider both local and global graph properties. The kernel maps graphs to feature vectors based on the k-dimensional Weisfeiler-Lehman algorithm. Approximation algorithms using adaptive sampling are introduced to make the kernel scalable to large graphs. Experimental results on graph classification benchmarks demonstrate the kernel achieves high accuracy while having fast running times.

1. Glocalized Weisfeiler-Lehman Graph Kernels:
Local-Global Feature Maps of Graphs
IEEE ICDM 2017
Christopher Morris, Kristian Kersting, Petra Mutzel
20. November 2017
TU Dortmund University, Algorithm Engineering Group
TU Darmstadt, Machine Learning Group

2. Motivation
Question
How similar are two graphs?
(a) Sildenafil (b) Vardenafil
1

3. High-level View: Supervised Graph Classification
2

4. High-level View: Supervised Graph Classification
⊆ H
φ: G → H
2

5. High-level View: Supervised Graph Classification
⊆ H
φ: G → H
2

6. Primer on Graph Kernels
Question
How similar are two graphs?
3

7. Primer on Graph Kernels
Question
How similar are two graphs?
Definition (Graph Kernel)
Let 𝒢 be a non-empty set of graphs and let k: 𝒢 × 𝒢 → R. Then k is
a graph kernel if there is a Hilbert space ℋ and a feature map
𝜑: 𝒢 → ℋ such that k(G, H) = ⟨𝜑(G), 𝜑(H)⟩.
3

8. Example: Weisfeiler-Lehman Subtree Kernel
Idea
Graph kernel based on well-known heuristic for graph
isomorphism testing: 1-WL or color refinement
Iteration: Two vertices get same colors iff if they have the same
colored neighborhood
N. Shervashidze, P. Schweitzer, E. J. van Leeuwen, K. Mehlhorn, and K. M. Borgwardt.
“Weisfeiler-Lehman Graph Kernels”. In: Journal of Machine Learning Research 12 (2011),
pp. 2539–2561 4

9. Example: Weisfeiler-Lehman Subtree Kernel
Idea
Graph kernel based on well-known heuristic for graph
isomorphism testing: 1-WL or color refinement
Iteration: Two vertices get same colors iff if they have the same
colored neighborhood
𝜑(G1) = ( )
(a) G1
𝜑(G2) = ( )
(b) G2
N. Shervashidze, P. Schweitzer, E. J. van Leeuwen, K. Mehlhorn, and K. M. Borgwardt.
“Weisfeiler-Lehman Graph Kernels”. In: Journal of Machine Learning Research 12 (2011),
pp. 2539–2561 4

10. Example: Weisfeiler-Lehman Subtree Kernel
Idea
Graph kernel based on well-known heuristic for graph
isomorphism testing: 1-WL or color refinement
Iteration: Two vertices get same colors iff if they have the same
colored neighborhood
𝜑(G1) = (2, 2, 2, )
(a) G1
𝜑(G2) = (1, 1, 3, )
(b) G2
N. Shervashidze, P. Schweitzer, E. J. van Leeuwen, K. Mehlhorn, and K. M. Borgwardt.
“Weisfeiler-Lehman Graph Kernels”. In: Journal of Machine Learning Research 12 (2011),
pp. 2539–2561 4

11. Example: Weisfeiler-Lehman Subtree Kernel
Idea
Graph kernel based on well-known heuristic for graph
isomorphism testing: 1-WL or color refinement
Iteration: Two vertices get same colors iff if they have the same
colored neighborhood
𝜑(G1) = (2, 2, 2, 2, 2, 2, 0, 0)
(a) G1
𝜑(G2) = (1, 1, 3, 2, 0, 1, 1, 1)
(b) G2
N. Shervashidze, P. Schweitzer, E. J. van Leeuwen, K. Mehlhorn, and K. M. Borgwardt.
“Weisfeiler-Lehman Graph Kernels”. In: Journal of Machine Learning Research 12 (2011),
pp. 2539–2561 4

12. Global vs. Local Graph Properties
Observation
Most graph kernels only take local graph properties into account,
e.g., they look at h-neighborhood around vertices.
h
5

13. Global vs. Local Graph Properties
Observation
Most graph kernels only take local graph properties into account,
e.g., they look at h-neighborhood around vertices.
h
Challenge
Design a scalable graph kernel that can take local as well global
graph properties into account.
5

14. Talk Structure
1 k-Dimensional Weisfeiler-Lehman
2 A Local Kernel Based on the k-dim. WL
3 Approximation Algorithms
4 Experimental Evaluation
6

15. k-Dimensional Weisfeiler-Lehman
k-dimensional Weisfeiler-Lehman
• Colors vertex tuples from Vk
• Two tuples v, w are i-neighbors if vj = wj for all j ̸= i
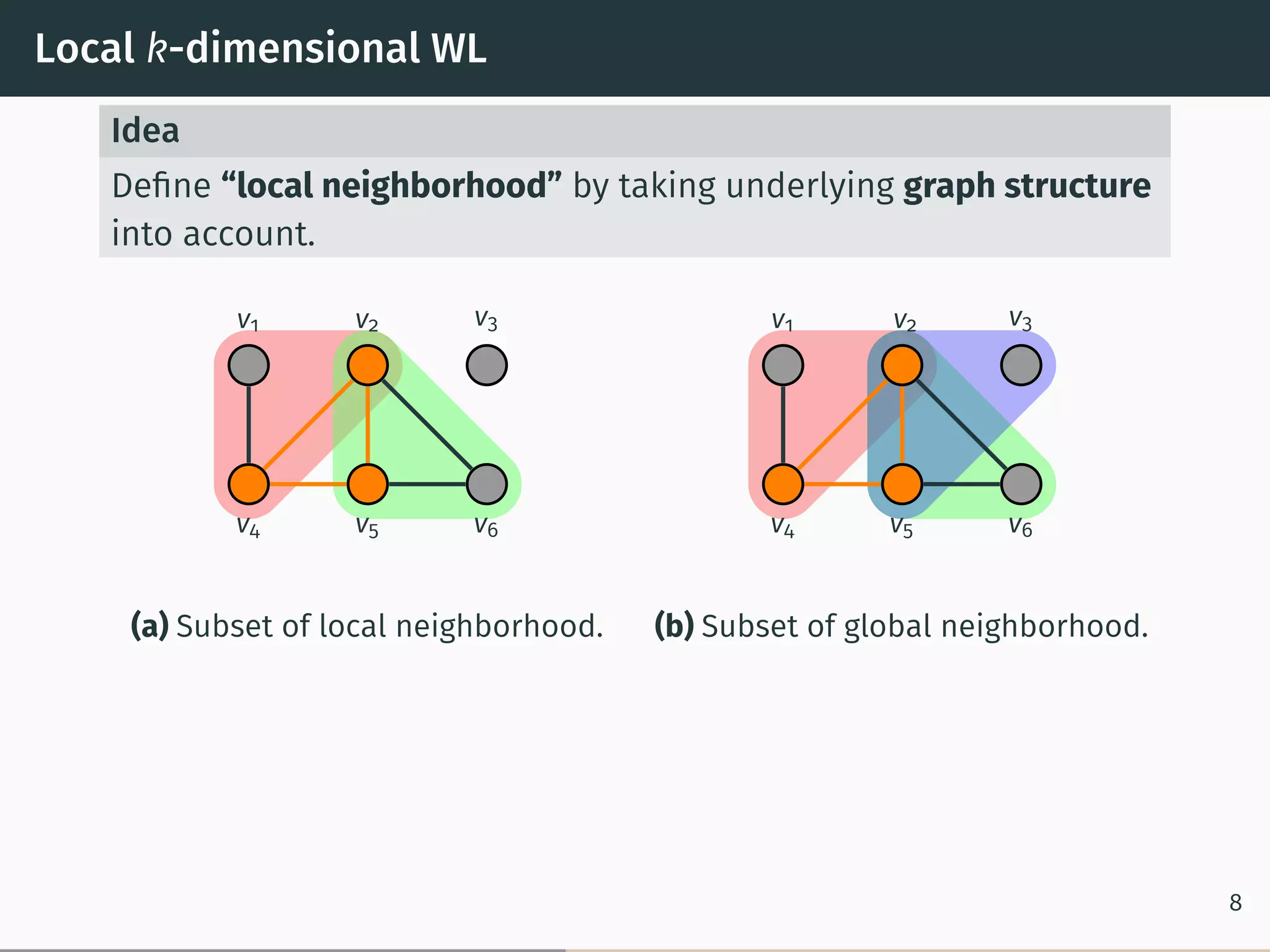
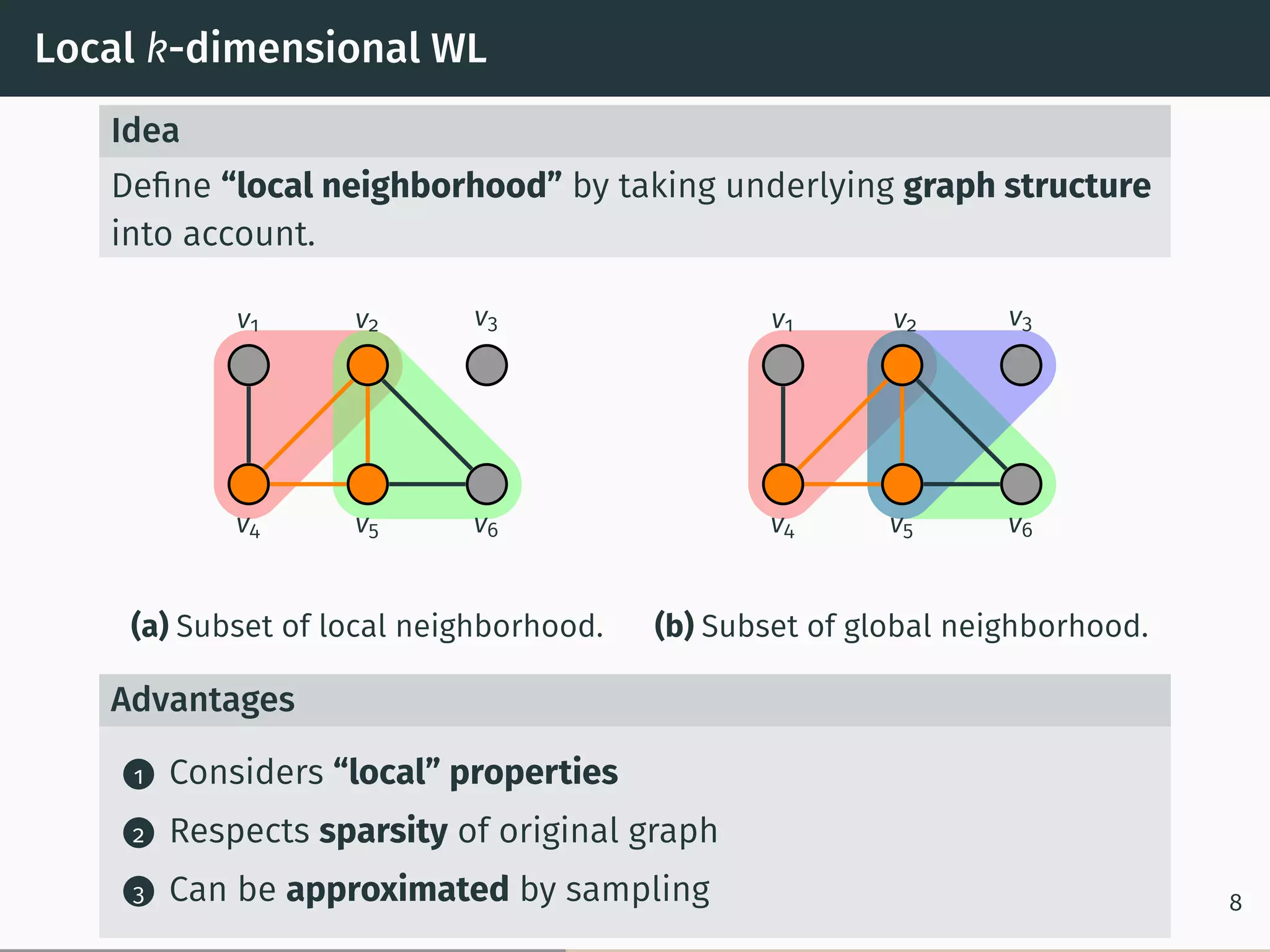
Idea of the Algorithm
Initially Initially two k-tuples v, w get the same color if vi ↦→ wi
induces a (graph) isomorphism between G[v] and G[w]
Iteration Two tuples with the same color get different colors if
there exists a color c and 1 ≤ i ≤ k such that v and w
have different i-neighbors of color c 7

16. Local k-dimensional WL
Idea
Define “local neighborhood” by taking underlying graph structure
into account.
8

17. Local k-dimensional WL
Idea
Define “local neighborhood” by taking underlying graph structure
into account.
v1 v2 v3
v4 v5 v6
(a) Subset of local neighborhood.
v1 v2 v3
v4 v5 v6
(b) Subset of global neighborhood.
8

18. Local k-dimensional WL
Idea
Define “local neighborhood” by taking underlying graph structure
into account.
v1 v2 v3
v4 v5 v6
(a) Subset of local neighborhood.
v1 v2 v3
v4 v5 v6
(b) Subset of global neighborhood.
Advantages
1 Considers “local” properties
2 Respects sparsity of original graph
3 Can be approximated by sampling 8

19. Scalability: Approximation by Sampling
Problem
Algorithm does not scale.
9

20. Scalability: Approximation by Sampling
Problem
Algorithm does not scale.
Solution
Approximate feature vector after h iterations by sampling.
9

21. Scalability: Approximation by Sampling
Problem
Algorithm does not scale.
Solution
Approximate feature vector after h iterations by sampling.
Highlevel Idea of Algorithm
1 Sample a number of subsets of size k
2 Explore h-neighborhood around each such set
3 Compute algorithm on each h-neighborhood
9

22. Scalability: Approximation by Sampling
Question
Why does this lead to correct results?
10

23. Scalability: Approximation by Sampling
Question
Why does this lead to correct results?
t
1
2
3
0
Insight
Color of central k-set t after h iterations is correct. 10

24. Scalability: Approximation by Sampling
Theorem (Informal)
With high probability the sampling algorithm approximates the
(normalized) feature vector of the local k-dimension WL such that
⃦
⃦
⃦̂︀𝜑k-LWL(G) − ̃︀𝜑k-LWL(G)
⃦
⃦
⃦
1
≤ 𝜀1 .
For bounded-degree graphs the running time is independent of the
size of the graph, i.e. the number of nodes and edges.
11

25. Scalability: Approximation by Sampling
Theorem (Informal)
Given a finite set 𝒢 of graphs. With high probability the sampling
algorithm approximate the kernel function of the local k-dimension
WL such that
sup
G,H∈𝒢
⃒
⃒
⃒̂︀kh
k-LWL(G, H) − ̃︀kh
k-LWL(G, H)
⃒
⃒
⃒ ≤ 𝜖2 .
For bounded-degree graphs the running time is independent of the
size of the graph, i.e. the number of nodes and edges.
12

26. Scalability: Approximation by Sampling
Problems
1 Algorithm is restricted to bounded-degree graphs!
2 How do we compute the sample size for general graphs?
13

27. Scalability: Approximation by Sampling
Problems
1 Algorithm is restricted to bounded-degree graphs!
2 How do we compute the sample size for general graphs?
Solution: Adaptive Sampling Algorithm
while Desired accurracy is not reached do
Increase sample size
Compute h neighborhoods for new sample
Compute algorithm in each h-neighborhood
end while
13

28. Scalability: Approximation by Adaptive Sampling
Theorem (Informal)
Let G be a graph, then the above procedure approximates the
normalized feature vector ̂︀𝜑k-LWL(G) of the k-LWL for h iterations
such that with high probability
sup
l∈Σ
⃒
⃒
⃒̂︀𝜑k-LWL(G)l − ̃︀𝜑k-LWL(G)l
⃒
⃒
⃒ ≤ 𝜀3 .
14

29. Scalability: Approximation by Adaptive Sampling
Theorem (Informal)
Let G be a graph, then the above procedure approximates the
normalized feature vector ̂︀𝜑k-LWL(G) of the k-LWL for h iterations
such that with high probability
sup
l∈Σ
⃒
⃒
⃒̂︀𝜑k-LWL(G)l − ̃︀𝜑k-LWL(G)l
⃒
⃒
⃒ ≤ 𝜀3 .
Remark
Proof relies on self-bounding properties of bounds based on
conditional Rademacher Averages.
14

30. Experimental Evaluation: Classification Accurary
PROTEINS
REDDIT
ENZYMES
IMDB-BINARY NCI1
MUTAG
0
10
20
30
40
50
60
70
80
90ClassificationAccuracy
3-LWL
1-LWL
3-GWL
15

31. Experimental Evaluation: Running Times
3-LWL-SP(0.1)
3-LWL-S(0.1)
3-LWL-SP(0.05)
3-LWL-S(0.05)
3-LWL-L
3-LWL-P
3-LWL
Algorithm
0
1000
2000
3000
4000
5000
6000
7000
8000
RunningTimes[s]
PROTEINS
16

32. Conclusion
1 Graph kernel based on k-dimensional Weisfeiler-Lehman
• Considers local as well as global graph properties
2 Approximation algorithms based on sampling
• Constant running time for bounded-degree graphs
• Adaptive sampling algorithm for general graphs
3 Promising experimental results
Collection of Graph Classification Benchmarks
graphkernels.cs.tu-dortmund.de
17