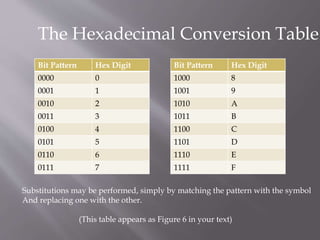
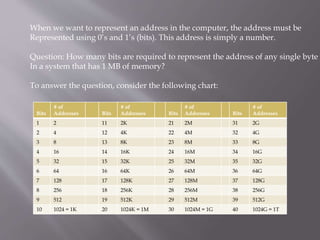
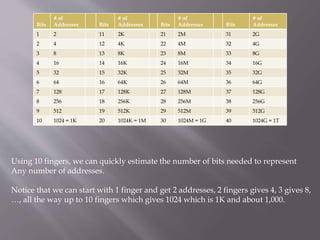
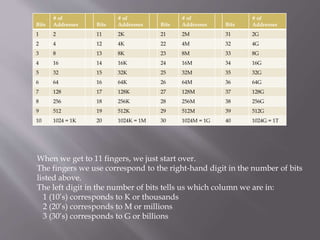
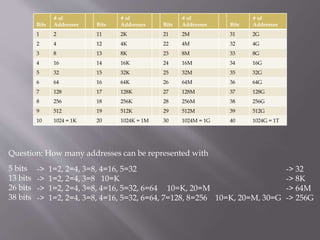
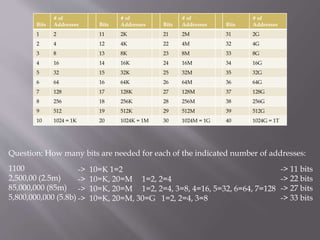
The document explains the organization of memory using binary digits (bits) and the conversion of binary sequences to hexadecimal notation for easier representation. It discusses the concept of memory addressing, detailing how bits are grouped into bytes and nibbles, and how to calculate memory capacity in units like kilobytes, megabytes, gigabytes, and terabytes. The document also includes a chart to estimate the number of bits needed to represent various numbers of addresses.

1. The Organization of Memory

2. The symbols Zero (0) and One (1) generically represent what is in memory
• Zeros and Ones are the digits used in the binary number system
• Hence, 0 and 1 are Binary digITs or BITS (for short)
• Computer memory consists of large numbers of bits
• These bits are organized into units called cells, which contain multiple bits
• In modern usage, these cells are often referred to as BYTEs
• By standard usage, a BYTE consists of 8 BITS

3. As we think about the organization of bits in a cell, it is useful to think of
these bits as representing a number. Consider the following cell:
Most significant bit (MSB)
Or
High-order end
Least significant bit (LSB)
Or
Low-order end
b7 b6 b5 b4 b3 b2 b1 b0

4. Imagine you are asked to copy the following sequence of bits:
1011011111111000000000000000101010100010110101001010
It is conceivable that you would make a mistake when writing this down or
A mistake might be made when reading it.
Why might this be so?

5. Possible reasons:
• Number of digits to be recorded and/or read
• Lack of variety

6. To overcome this, we introduce a system that provides us with a
Shorthand Method for communicating and/or representing
Binary information:
Hexadecimal Digits

7. Hexadecimal Digits
• Hexadecimal means 16
• It is a system of numbers consisting of 16 symbol
• The symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
• We are able to associate each of these symbols with a unique 4-bit pattern
• By doing this, we can replace these patterns in a bit string with their equivalent
Hexadecimal digit symbols to shorten the information and add more variety.

8. The Hexadecimal Conversion Table
Bit Pattern Hex Digit
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
Bit Pattern Hex Digit
1000 8
1001 9
1010 A
1011 B
1100 C
1101 D
1110 E
1111 F
Substitutions may be performed, simply by matching the pattern with the symbol
And replacing one with the other.
(This table appears as Figure 6 in your text)

9. Example: Consider the bit string we presented earlier
1011011111111000000000000000101010100010110101001010
Starting from the right, we will divide this into 4-bit patterns:
1011 0111 1111 1000 0000 0000 0000 1010 1010 0010 1101 0100 1010
Replace each 4-bit pattern with an equivalent Hex Digit (using the table for now)
1011 0111 1111 1000 0000 0000 0000 1010 1010 0010 1101 0100 1010
B 7 F 8 0 0 0 A A 2 D 4 A
The equivalent hex string for this sequence is : B7F8000AA2D4A

10. To reverse the process, we look up each hex digit and replace it with a 4 bit pattern
Given the hex string: B7F8000AA2D4A
B 7 F 8 0 0 0 A A 2 D 4 A
1011 0111 1111 1000 0000 0000 0000 1010 1010 0010 1101 0100 1010

11. Question: What if the bit string only contains 11 bits or something not
evenly divisible by 4?
Answer: Add 0’s on the left until the number of bits is divisible by 4
Question: How do you know how many bits should be in the answer when
Converting from hex to binary?
Answer: You must be told how many bits are in the answer and drop the necessary
Number of leading zeros after doing the conversion to get the correct final bit string.

12. Question: Why do we use Hexadecimal?
Answer: It is a convenient shorthand for binary information
Generally, when binary information is presented to you,
it will be presented using hexadecimal notation.

13. Now that we have looked at the basic organization of memory and
the representation of bit strings using hexadecimal, we turn to the concept
Of Memory capacities and the related concept of Memory addressing.

14. As noted before, 1 bit is a single 0 or a single 1
We group bits together into cells, usually consisting of 8 bits
In standard practice, 8 bits forms 1 byte of memory.
Question: What do you call “Half a byte”?
Answer: a nibble
Note: a nibble is 4 bits - enough bits to be represented by a single hex
digit
so 1 byte is 2 nibbles, and its value can be represented by
2 hex digits.
Generally, 1 byte is the smallest unit of memory that is addressable
If we think of bytes as P O Boxes, we can think of an address as a Box Number
An address allows us to uniquely identify any single byte in memory.

15. A byte of memory does not give us much capability. We ordinarily need many
Bytes to represent the kinds of information we are interested.
In fact we need
Thousands of bytes (kilobytes - abbreviated KB), or
Millions of bytes (megabytes - abbreviated MB) or
Billions of bytes (gigabytes - abbreviated GB) or even
Trillions of bytes (terabytes - abbreviated TB) or more

16. When we want to represent an address in the computer, the address must be
Represented using 0’s and 1’s (bits). This address is simply a number.
Question: How many bits are required to represent the address of any single byte
In a system that has 1 MB of memory?
To answer the question, consider the following chart:
Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses
1 2 11 2K 21 2M 31 2G
2 4 12 4K 22 4M 32 4G
3 8 13 8K 23 8M 33 8G
4 16 14 16K 24 16M 34 16G
5 32 15 32K 25 32M 35 32G
6 64 16 64K 26 64M 36 64G
7 128 17 128K 27 128M 37 128G
8 256 18 256K 28 256M 38 256G
9 512 19 512K 29 512M 39 512G
10 1024 = 1K 20 1024K = 1M 30 1024M = 1G 40 1024G = 1T

17. Using 10 fingers, we can quickly estimate the number of bits needed to represent
Any number of addresses.
Notice that we can start with 1 finger and get 2 addresses, 2 fingers gives 4, 3 gives 8,
…, all the way up to 10 fingers which gives 1024 which is 1K and about 1,000.
Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses
1 2 11 2K 21 2M 31 2G
2 4 12 4K 22 4M 32 4G
3 8 13 8K 23 8M 33 8G
4 16 14 16K 24 16M 34 16G
5 32 15 32K 25 32M 35 32G
6 64 16 64K 26 64M 36 64G
7 128 17 128K 27 128M 37 128G
8 256 18 256K 28 256M 38 256G
9 512 19 512K 29 512M 39 512G
10 1024 = 1K 20 1024K = 1M 30 1024M = 1G 40 1024G = 1T

18. Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses
1 2 11 2K 21 2M 31 2G
2 4 12 4K 22 4M 32 4G
3 8 13 8K 23 8M 33 8G
4 16 14 16K 24 16M 34 16G
5 32 15 32K 25 32M 35 32G
6 64 16 64K 26 64M 36 64G
7 128 17 128K 27 128M 37 128G
8 256 18 256K 28 256M 38 256G
9 512 19 512K 29 512M 39 512G
10 1024 = 1K 20 1024K = 1M 30 1024M = 1G 40 1024G = 1T
When we get to 11 fingers, we just start over.
The fingers we use correspond to the right-hand digit in the number of bits
listed above.
The left digit in the number of bits tells us which column we are in:
1 (10’s) corresponds to K or thousands
2 (20’s) corresponds to M or millions
3 (30’s) corresponds to G or billions

19. Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses
1 2 11 2K 21 2M 31 2G
2 4 12 4K 22 4M 32 4G
3 8 13 8K 23 8M 33 8G
4 16 14 16K 24 16M 34 16G
5 32 15 32K 25 32M 35 32G
6 64 16 64K 26 64M 36 64G
7 128 17 128K 27 128M 37 128G
8 256 18 256K 28 256M 38 256G
9 512 19 512K 29 512M 39 512G
10 1024 = 1K 20 1024K = 1M 30 1024M = 1G 40 1024G = 1T
Question: How many addresses can be represented with
5 bits
13 bits
26 bits
38 bits
-> 1=2, 2=4, 3=8, 4=16, 5=32
-> 1=2, 2=4, 3=8 10=K
-> 1=2, 2=4, 3=8, 4=16, 5=32, 6=64 10=K, 20=M
-> 1=2, 2=4, 3=8, 4=16, 5=32, 6=64, 7=128, 8=256 10=K, 20=M, 30=G
-> 32
-> 8K
-> 64M
-> 256G

20. Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses Bits
# of
Addresses
1 2 11 2K 21 2M 31 2G
2 4 12 4K 22 4M 32 4G
3 8 13 8K 23 8M 33 8G
4 16 14 16K 24 16M 34 16G
5 32 15 32K 25 32M 35 32G
6 64 16 64K 26 64M 36 64G
7 128 17 128K 27 128M 37 128G
8 256 18 256K 28 256M 38 256G
9 512 19 512K 29 512M 39 512G
10 1024 = 1K 20 1024K = 1M 30 1024M = 1G 40 1024G = 1T
Question: How many bits are needed for each of the indicated number of addresses:
1100
2,500,00 (2.5m)
85,000,000 (85m)
5,800,000,000 (5.8b)
-> 10=K 1=2
-> 10=K, 20=M 1=2, 2=4
-> 10=K, 20=M 1=2, 2=4, 3=8, 4=16, 5=32, 6=64, 7=128
-> 10=K, 20=M, 30=G 1=2, 2=4, 3=8
-> 11 bits
-> 22 bits
-> 27 bits
-> 33 bits