Data representation

1. Data Representation – Numbers

2. Basic Binary
1 = switch closed / electricity on, 0 = switch open / electricity off
If you send 1 bit, how many different combinations can you send?
1 or 0
If you send 2 bits, how many different combinations can you sent?
00 01 10 11
3 bits? 000 001 010 011 etc
4 bits? 0000 0001 0010 0011 0100 etc.
5 bits? 00001 00010 00011 00100 etc.

3. Terminology
Bit 1 or 0
Nibbl
e
4 bits
Byte 2 nibbles / 8 bits
KB Kilobyte 1000/1024 bytes
MB Megabyte 1000/1024 KB
GB Gigabyte 1000/1024 MB
TB Terabyte 1000/1024 GB

4. Binary - Decimal
128 64 32 16 8 4 2 1
0 0 0 0 1 0 0 1
8 1 = 9
128 64 32 16 8 4 2 1
1 0 1 0 0 1 1 0
128 32 4 2 = 166

5. Have a go
4 10011110
5 11111001
6 1011100101
7 11000000111
8 100101100101
9 1111001111010111
10 1000011100010110
128 64 32 16 8 4 2 1
0 0 1 1 0 0 0 1
128 64 32 16 8 4 2 1
1 0 0 1 1 0 1 0
128 64 32 16 8 4 2 1
1 1 1 1 0 1 1 1
1
2
3
Answers: 1 = 49, 2 = 154, 3 = 247, 4 = 158, 5 = 249, 6 = 741, 7 = 1543, 8 = 2405, 9 = 62423, 10 = 34582

6. Patterns
 If the least significant bit (right most) is a 1, the number is odd
 All 1s = the next number -1
e.g.
= 127 (is 128-1)
 The smallest number in positive binary is always 0
 The number of combinations is equal to the next number
e.g.
= 128 different combinations
0 to 127
12
8
64 32 16 8 4 2 1
0 1 1 1 1 1 1 1
12
8
64 32 16 8 4 2 1
0 1 1 1 1 1 1 1

7. Decimal - Binary
128 64 32 16 8 4 2 1
0 0 0 1 0 1 1 1
23
23 – 16 = 7
7 – 4 = 3
128 64 32 16 8 4 2 1
0 1 1 0 0 0 1 0
98
98 – 64 = 34
34 – 32 = 2
128 64 32 16 8 4 2 1
1 1 1 1 0 0 1 0
242
242 – 128 = 114
114 – 64 = 50
50 – 32 = 18
18 – 16 = 2

8. Have a go
6 220
7 269
8 612
9 2974
10 32651
Answers: 1 = 11100, 2 = 101011, 3 = 1001110, 4 = 1100101, 5 = 11001000,
6 = 11011100, 7 = 100001101, 8 = 1001100100, 9 = 101110011110, 10 = 111111110001011
1 28
2 43
3 78
4 101
5 200

9. Hexadecimal
 Easier to remember than binary
 Quicker/easier to write than binary
 Can be converted quickly to binary
(and back)
 Each nibble is converted into a single
hexadecimal number
1 nibble can be:
Decimal Hexadecimal
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10 A
11 B
12 C
13 D
14 E
15 F

10. Hexadecimal - binary
3A
3 A
0011 1010
00111010
F20
F 2 0
1111 0010 0000
111100100000

11. Have a go, hex-bin
1 11
2 2A
3 BB
4 6C
5 A0
6 50F
7 9BD
8 D5AA
9 1974
10 26ABEB
Answers: 1 = 00010001, 2 = 00101010, 3 = 10111011, 4 = 01101100, 5 = 10100000, 6 = 010100001111,
7 = 100110111101, 8 = 1101010110101010, 9 = 0001100101110100, 10 = 001001101010101111101011

12. Binary - Hexadecimal
10011110
1001 1110
9 14
9E
111101011011
1111 0101 1011
15 5 11
F5B

13. Have a go, binary-hex
1 01100001
2 10111111
3 10000000
4 01011111
5 111001101011
6 001010101100
7 111100001111
8 001100111111
9 0101111000101011
10 1111111100010110
Answers: 1 = 6A, 2 = BF, 3 = 80, 4 = 5F, 5 = E6B, 6 = 2AC, 7 = F0F, 8 = 33F, 9 =
5E2B, 10 = FF16

14. Hexadecimal - Decimal
 Convert to binary and then to decimal…
 Or…
162
161
160
(3 * 16) + (10 * 1) = 58
161
160
3 A
162
161
160
1 D 3
3A
=
(1 * 16 * 16 ) + (13 * 16) + (3 * 1) =
467
1D3
=
256 16 1

15. Have a go, hex-dec
Answers: 1 = 17, 2 = 42, 3 = 187, 4 = 108, 5 = 160, 6 = 1295, 7 = 2493, 8 = 54698, 9 = 6516, 10 =
2534379
1 11
2 2A
3 BB
4 6C
5 A0
6 50F
7 9BD
8 D5AA
9 1974
10 26ABEB

16. Decimal – Hexadecimal
 Convert to binary and then hexa
 Or
162
161
160
256 16 1
0 4 14
78
= 4E
199
= C7
299
= 12B
256 16 1
0 12 7
256 16 1
1 2 11

17. Have a go – dec-hex
Answers: 1 = 16, 2 = 3B, 3 = 64, 4 = BD, 5 = E7, 6 = 101, 7 = 420, 8 = 7D0, 9 = DFA, 10 = 7EBC
1 22
2 59
3 100
4 189
5 231
6 257
7 1056
8 2000
9 3578
10 32444

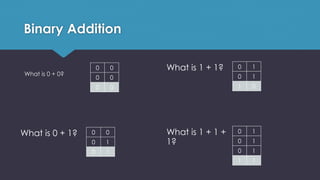
18. Binary Addition
What is 0 + 0?
0 0
0 0
0 0
What is 0 + 1? 0 0
0 1
0 1
What is 1 + 1? 0 1
0 1
1 0
What is 1 + 1 +
1?
0 1
0 1
0 1
1 1

19. Binary addition – 4 basic rules
0 + 0 = 0
0 + 1 = 1
1 + 1 = 0 carry 1
1 + 1 + 1 = 1 carry 1
Delete all boxes for
example
0 0 0 1
0 1 0 1
0 1 1 0
1
1 0 1 1
0 0 1 0
1 1 0 1
1
delete

20. 0 0 1 1 0 1 0 1
1 0 0 0 1 1 1 1
1 1 0 0 0 1 0 0
1 1 1 1 1 1
1 1 0 0 1 1 0 1
1 0 0 1 1 1 1 1
0 1 1 0 1 1 0 0
1 1 1 1 1
(1)
Overflow = the result of the addition
is too large to fit in 8 bits. A 9th
bit is
needed to store the result.

21. Have a go, binary addition
0 0 1 1 0 1 0 1
1 0 0 0 0 1 1 1
1 0 1 1 0 1 0 0
1 1 1
1 1 0 0 1 1 0 1
1 0 0 1 1 1 0 0
1 0 0 0 1 0 0 1
1 1 1
0 1 1 0 1 0 1 0
1 0 1 0 1 0 1 0
0 0 0 1 0 1 0 0
1 1 1 1
1 0 0 1 1 0 0 1
0 1 0 1 0 1 1 1
1 1 1 1 0 0 0 0
1 1 1 1 1
0 1 1 1 1 0 0 0
1 1 1 0 0 0 0 1
0 1 0 1 1 0 0 1
1 1
0 1 0 1 1 0 1 0
0 0 1 0 1 1 0 0
1 1 1 0 1 1 0 1
0 1 1 1 0 0 1 1
1 1 1 1
(1)
(1)
(1)
(1)
Delete boxes for answers

22. Binary Shifts
 Move binary numbers a set number of places to the left, or the right
 Logical shift – spaces are filled in with 0s
 Arithmetic shift – when shifting left the spaces are filled with 0s, when shifting right they are
filled with the MSB

23. Logical
0 0 1 1 0 0 0 1
Left shift 2 spaces
1 1 0 0 0 1 0 0
1 0 0 1 0 1 1 1
Right shift 2 spaces
0 0 1 0 0 1 0 1

24. Arithmetic
0 0 1 1 0 0 0 1
Left shift 2 spaces
1 1 0 0 0 1 0 0
1 0 0 1 0 1 1 1
Right shift 2 spaces
1 1 1 0 0 1 0 1

25. What do they do?
 Each left shift (log/ari) multiplies the number by 2 (so 3 shifts multiply by 2 x 2 x 2) etc.
 Each logical right shift divides the number by 2 (so 2 shifts divides by 4) etc.

26. Have a go, shifts
Type Left/Right Num Places Binary
1 Logical Left 1 01011010
2 Arithmetic Left 1 10101110
3 Logical Right 2 01011111
4 Logical Left 2 11110010
5 Logical Right 3 10111010
6 Arithmetic Left 3 00001110
7 Arithmetic Right 4 11010101
8 Logical Left 5 10101010
9 Logical Right 6 01111100
10 Arithmetic Right 6 10111111
Answers
10110100
01011100
00010111
11001000
00010111
01110000
11111101
01000000
00000001
11111110