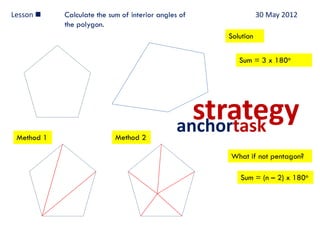
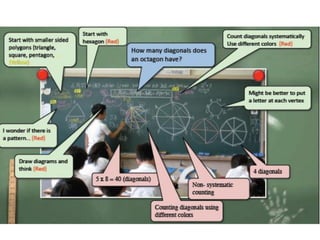
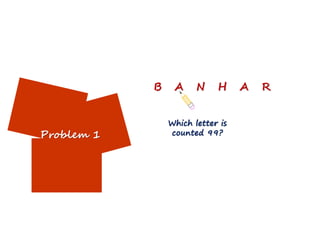
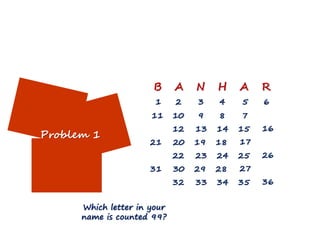
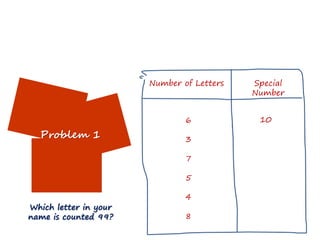
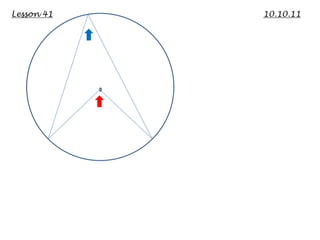
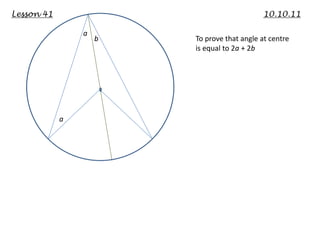
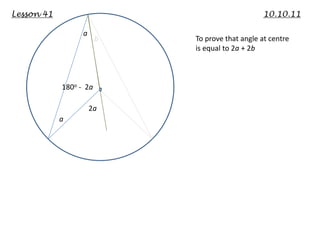
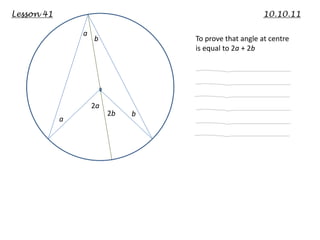
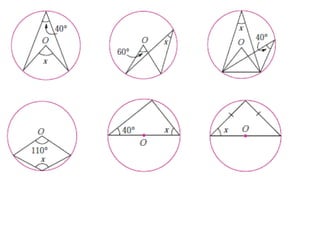
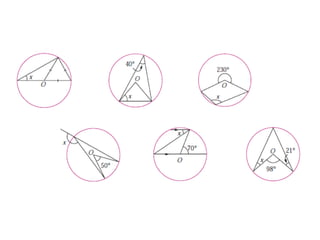
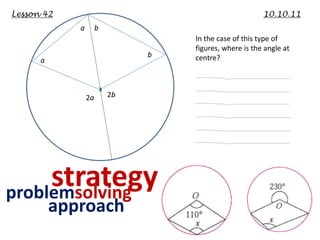
This lecture discusses strategies for incorporating reflection in mathematics classrooms. It provides examples of reflection techniques that can be used in both teacher-centered lessons like lectures as well as student-centered lessons like group work. Some strategies mentioned include using board writing, math journals, student explanations, self-assessments, problem-solving approaches, and questioning techniques to encourage students to re-examine their thinking. The goal is to promote deep learning through reflection on mathematical concepts and ideas.

1. Parallel Lecture
strategies
to incorporate
reflection
in the mathematics classroom
Ye a p B a n H a r  M a r s h a l l C a v e n d i s h I n s t i t u t e  P a t h l i g h t S c h o o l
Slides are available at www.banhar.blogspot.com

2. Without reflection, learning ends
"short of the re-organization
of thinking that deep learning
requires" (Ewell, 1997).
Synopsis
This lecture includes some examples of how
teachers can use strategies to encourage
reflection in mathematics lessons. The examples
covers lessons which are more teacher-centric
such as lectures as well as lessons which are more
student-centric such as group work.

3. strategies
 lesson organization
 lesson implementation
 lesson routine
 lesson philosophy

4. Lesson  Calculate the sum of interior angles of 30 May 2012
the polygon.
Solution
Sum = 3 x 180o
strategy
anchortask
Method 1 Method 2
What if not pentagon?
Sum = (n – 2) x 180o

6. strategy
boardwriting

7. strategy
mathsjournal

8. strategy
mathsjournal

10. B A N H A R
Problem 1

11. B A N H A R
Problem 1

12. B A N H A R
Problem 1

13. B A N H A R
Problem 1

14. B A N H A R
Problem 1

15. B A N H A R
Problem 1

16. B A N H A R
Problem 1

17. B A N H A R
Problem 1

18. B A N H A R
Problem 1

19. B A N H A R
Problem 1

20. B A N H A R
Problem 1

21. B A N H A R
Problem 1

22. B A N H A R
Problem 1

23. B A N H A R
Problem 1

24. B A N H A R
Problem 1

25. B A N H A R
Problem 1

26. B A N H A R
Problem 1

27. B A N H A R
Problem 1

28. B A N H A R
Problem 1

29. B A N H A R
Which letter is
Problem 1 counted 99?

30. B A N H A R
1 2 3 4 5 6
11 10 9 8 7
12 13 14 15 16
Problem 1
21 20 19 18 17
22 23 24 25 26
31 30 29 28 27
32 33 34 35 36
Which letter in your
name is counted 99?

31. Number of Letters Which Letter?
6 3rd
Problem 1 3 3rd
7 3rd
5 3rd
4 3rd ???
Which letter in your
name is counted 99? 8 1st

32. Number of Letters Special
Number
6 10
Problem 1 3
7
5
4
Which letter in your
name is counted 99? 8

33. Generalization is an
important aspect of
mathematics learning.
Reflect
What are some reflection
strategies used to develop
this competency?

34. King Solomon Academy, London

35. strategy
studentexplaining
King Solomon Academy, London

36. You have done _____ tasks. There are ______
mistakes. Please find and correct them before
ABC Secondary School ________
Name: Class
Solve the equations
1. 3x – 1 = 4
2. 3 – 4x = 1
3. 3x – 1 = 5x + 2
Re-organization of thinking:
• From doing to evaluating
Aspects of Reflection
• Reflection to check oneself
• Realizing the need to check oneself
strategy
selfassessment

38. Lesson 41 10.10.11

39. Lesson 41 10.10.11
a
b To prove that angle at centre
is equal to 2a + 2b
a

40. Northbrooks Secondary School, Singapore

41. Lesson 41 10.10.11
a
b To prove that angle at centre
is equal to 2a + 2b
180o - 2a
2a
a

42. Lesson 41 10.10.11
a
b To prove that angle at centre
is equal to 2a + 2b
2a
2b b
a

45. Lesson 42 10.10.11
a b
In the case of this type of
figures, where is the angle at
b centre?
a
2a 2b
strategy
problemsolving
approach

46. strategy
problemposing
strategy
questioningtechnique

48. Parallel Lecture
strategies
to incorporate
reflection
in the mathematics classroom
Ye a p B a n H a r  M a r s h a l l C a v e n d i s h I n s t i t u t e  P a t h l i g h t S c h o o l
Slides are available at www.banhar.blogspot.com