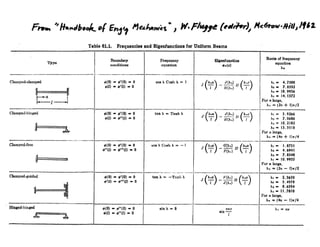
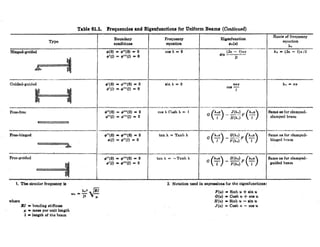
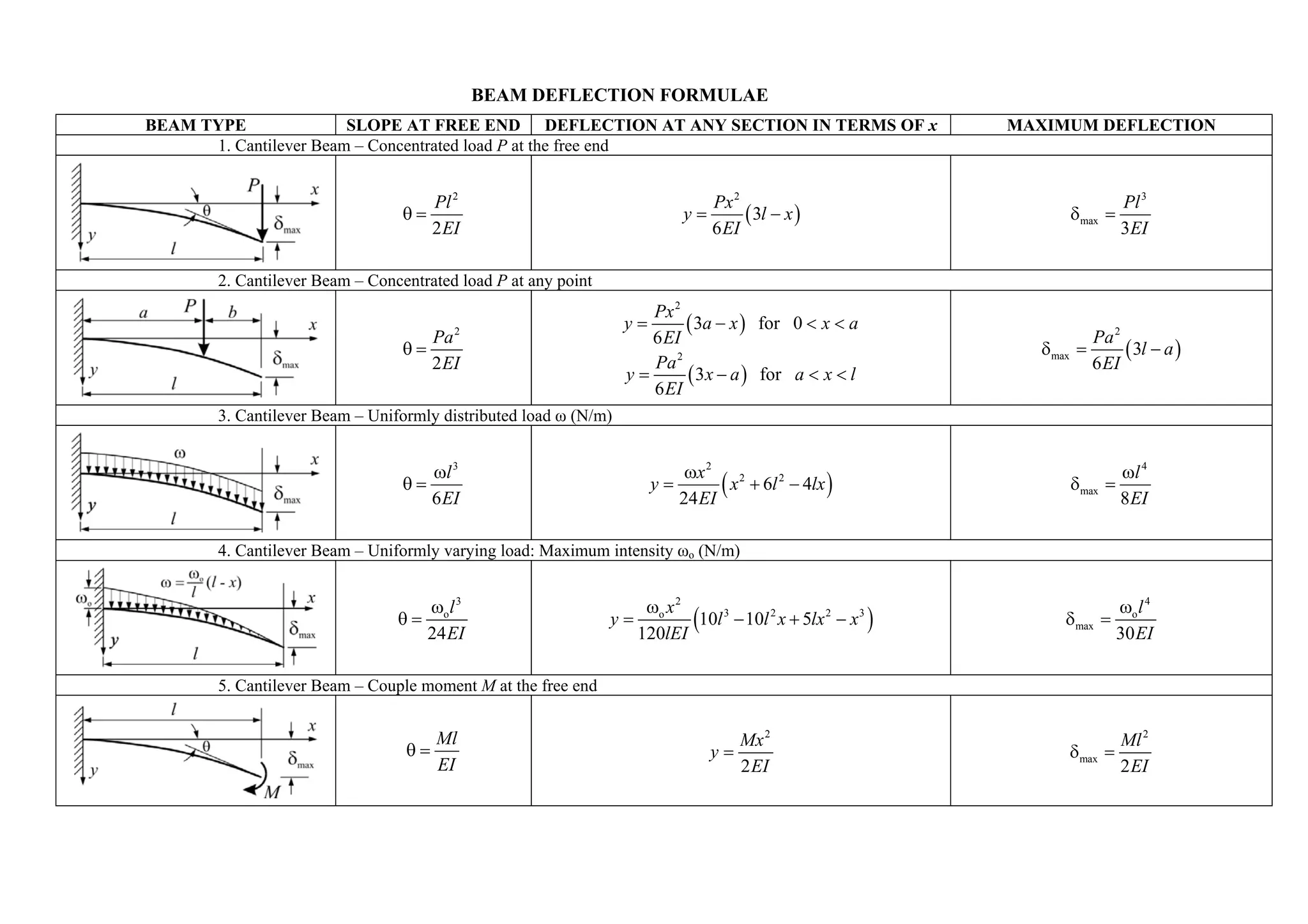
The document provides formulae for calculating slope and deflection of beams under different loading conditions: 1) It gives equations for calculating slope at free ends and deflection at any section for cantilever beams with various loads including concentrated load, uniform load, and uniformly varying load. 2) Equations are also provided for simply supported beams with the same loading types to determine slope at supports and maximum deflection in the center or at load location. 3) The document contains 10 sections that list the beam type, applied load, formulae for slope at free ends or supports, and expressions for deflection along the beam and point of maximum deflection.

1. BEAM DEFLECTION FORMULAE
BEAM TYPE SLOPE AT FREE END DEFLECTION AT ANY SECTION IN TERMS OF x MAXIMUM DEFLECTION
1. Cantilever Beam – Concentrated load P at the free end
2
2
Pl
EI
θ = ( )
2
3
6
Px
y l x
EI
= −
3
max
3
Pl
EI
δ =
2. Cantilever Beam – Concentrated load P at any point
2
2
Pa
EI
θ =
( )
2
3 for 0
6
Px
y a x x a
EI
= − < <
( )
2
3 for
6
Pa
y x a a x l
EI
= − < <
( )
2
max 3
6
Pa
l a
EI
δ = −
3. Cantilever Beam – Uniformly distributed load ω (N/m)
3
6
l
EI
ω
θ = ( )
2
2 2
6 4
24
x
y x l lx
EI
ω
= + −
4
max
8
l
EI
ω
δ =
4. Cantilever Beam – Uniformly varying load: Maximum intensity ωo (N/m)
3
o
24
l
EI
ω
θ = ( )
2
3 2 2 3o
10 10 5
120
x
y l l x lx x
lEI
ω
= − + −
4
o
max
30
l
EI
ω
δ =
5. Cantilever Beam – Couple moment M at the free end
Ml
EI
θ =
2
2
Mx
y
EI
=
2
max
2
Ml
EI
δ =

2. BEAM DEFLECTION FORMULAS
BEAM TYPE SLOPE AT ENDS DEFLECTION AT ANY SECTION IN TERMS OF x MAXIMUM AND CENTER
DEFLECTION
6. Beam Simply Supported at Ends – Concentrated load P at the center
2
1 2
16
Pl
EI
θ = θ =
2
23
for 0
12 4 2
Px l l
y x x
EI
⎛ ⎞
= − < <⎜ ⎟
⎝ ⎠
3
max
48
Pl
EI
δ =
7. Beam Simply Supported at Ends – Concentrated load P at any point
2 2
1
( )
6
Pb l b
lEI
−
θ =
2
(2 )
6
Pab l b
lEI
−
θ =
( )2 2 2
for 0
6
Pbx
y l x b x a
lEI
= − − < <
( ) ( )3 2 2 3
6
for
Pb l
y x a l b x x
lEI b
a x l
⎡ ⎤
= − + − −⎢ ⎥⎣ ⎦
< <
( )
3 22 2
max
9 3
Pb l b
lEI
−
δ = at ( )2 2
3x l b= −
( )2 2
at the center, if3 4
48
Pb
l b
EI
δ = − a b>
8. Beam Simply Supported at Ends – Uniformly distributed load ω (N/m)
3
1 2
24
l
EI
ω
θ = θ = ( )3 2 3
2
24
x
y l lx x
EI
ω
= − +
4
max
5
384
l
EI
ω
δ =
9. Beam Simply Supported at Ends – Couple moment M at the right end
1
6
Ml
EI
θ =
2
3
Ml
EI
θ =
2
2
1
6
Mlx x
y
EI l
⎛ ⎞
= −⎜ ⎟
⎝ ⎠
2
max
9 3
Ml
EI
δ = at
3
l
x =
2
16
Ml
EI
δ = at the center
10. Beam Simply Supported at Ends – Uniformly varying load: Maximum intensity ωo (N/m)
3
o
1
7
360
l
EI
ω
θ =
3
o
2
45
l
EI
ω
θ =
( )4 2 2 4o
7 10 3
360
x
y l l x x
lEI
ω
= − +
4
o
max 0.00652
l
EI
ω
δ = at 0.519x l=
4
o
0.00651
l
EI
ω
δ = at the center

3. file:///G|/BACKUP/Courses_and_seminars/0MAE4770S12/url%20for%20beam%20formulas.txt[1/23/2012 12:15:35 PM]
http://www.advancepipeliner.com/Resources/Others/Beams/Beam_Deflection_Formulae.pdf