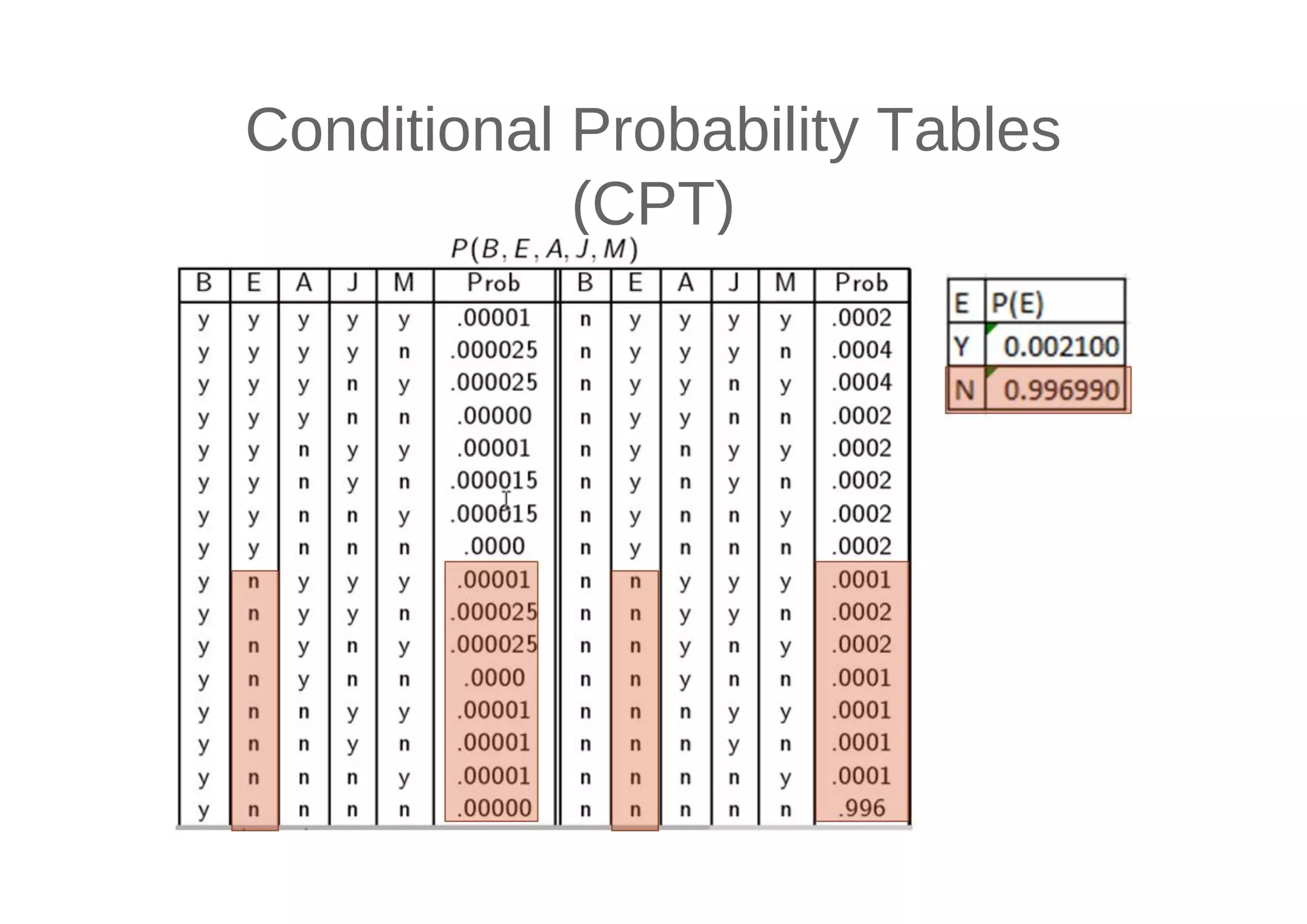
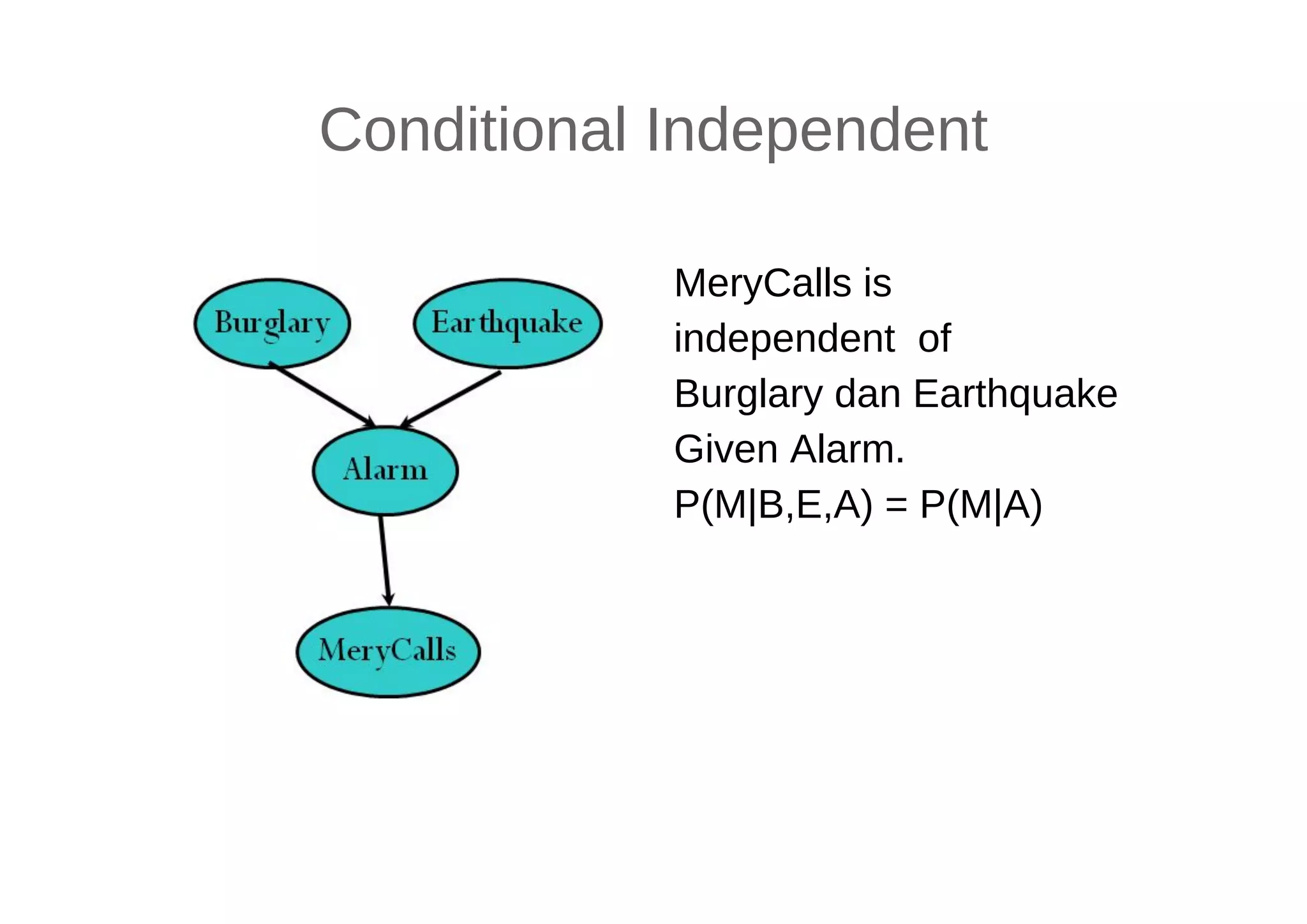
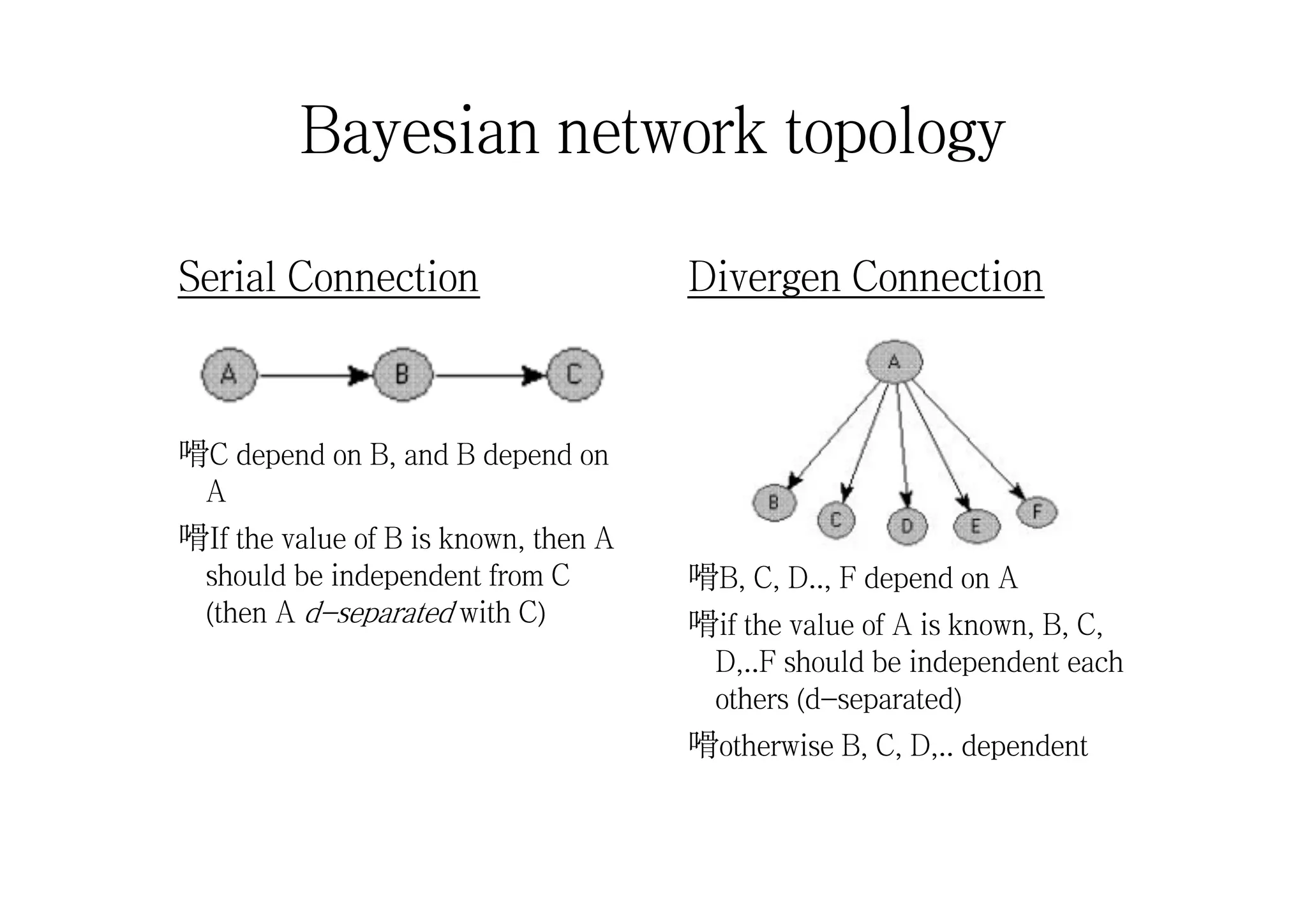
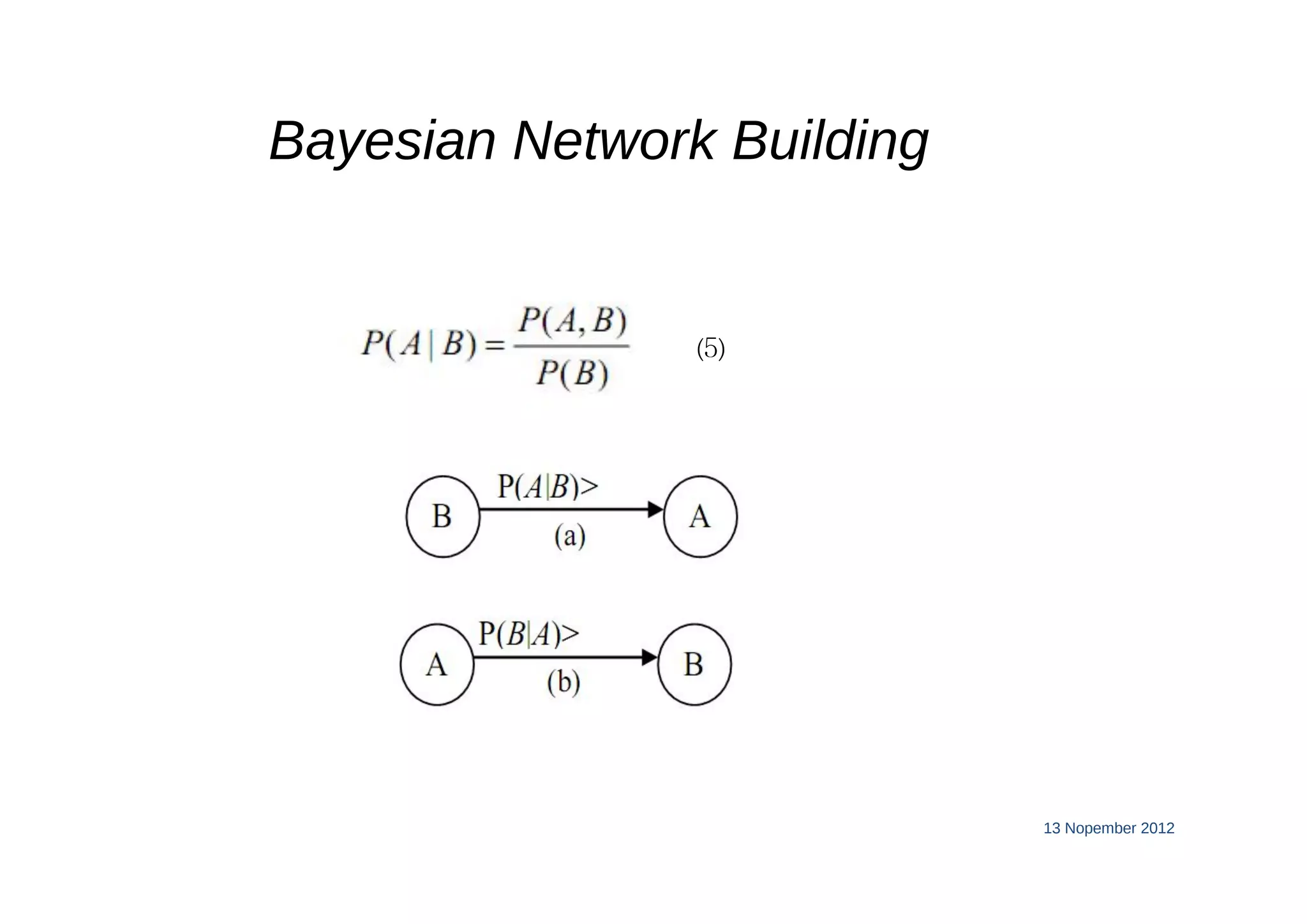
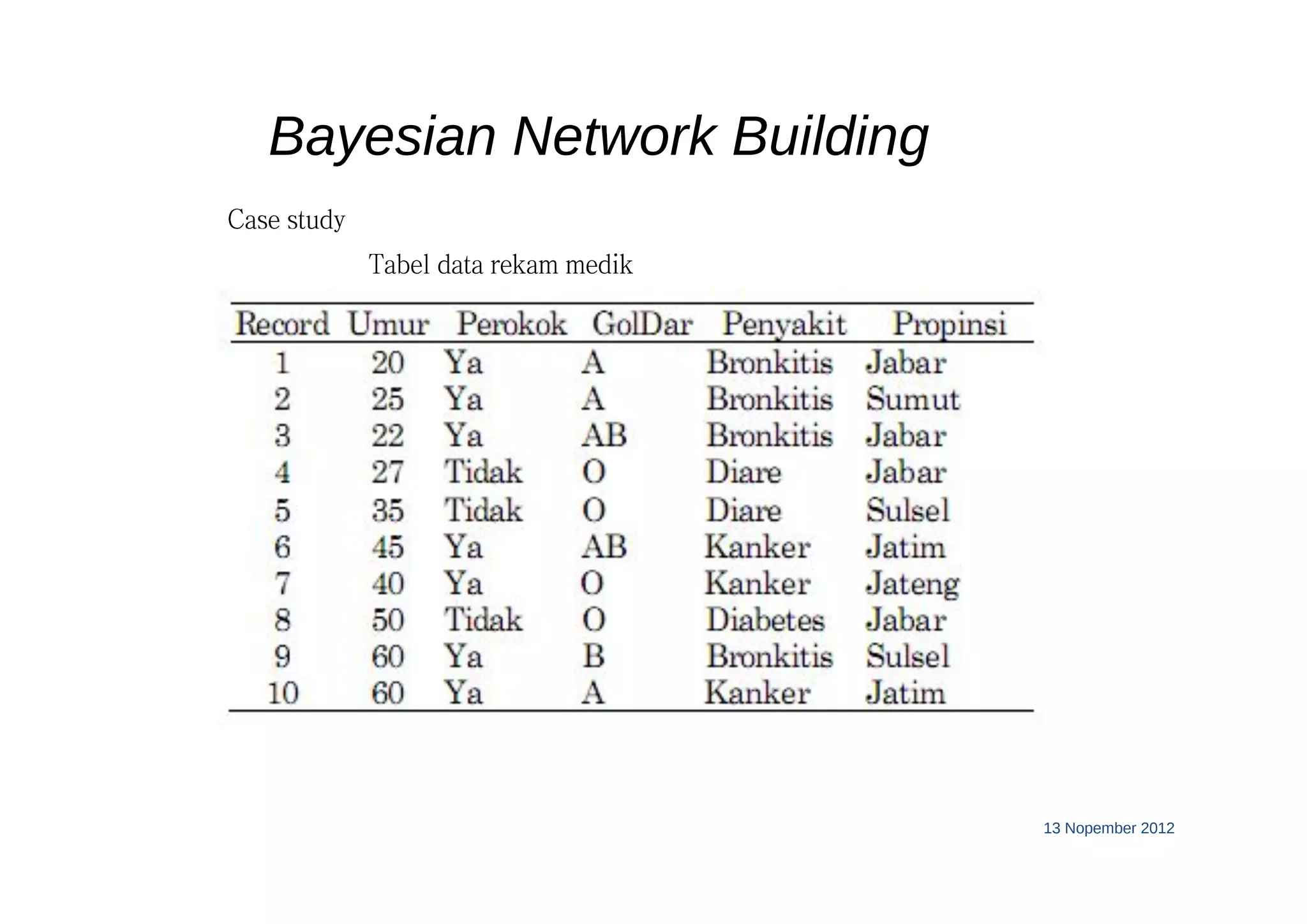
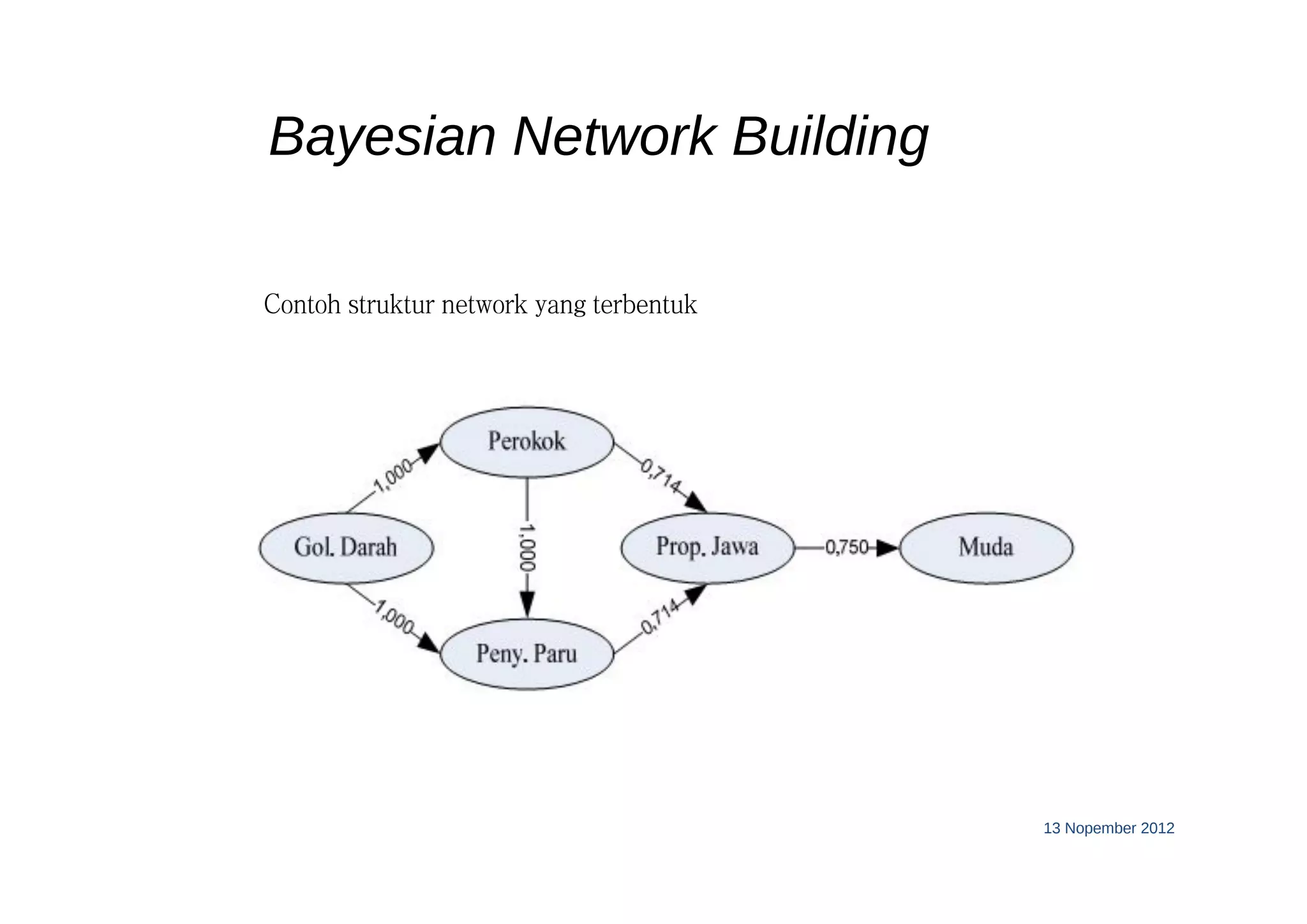
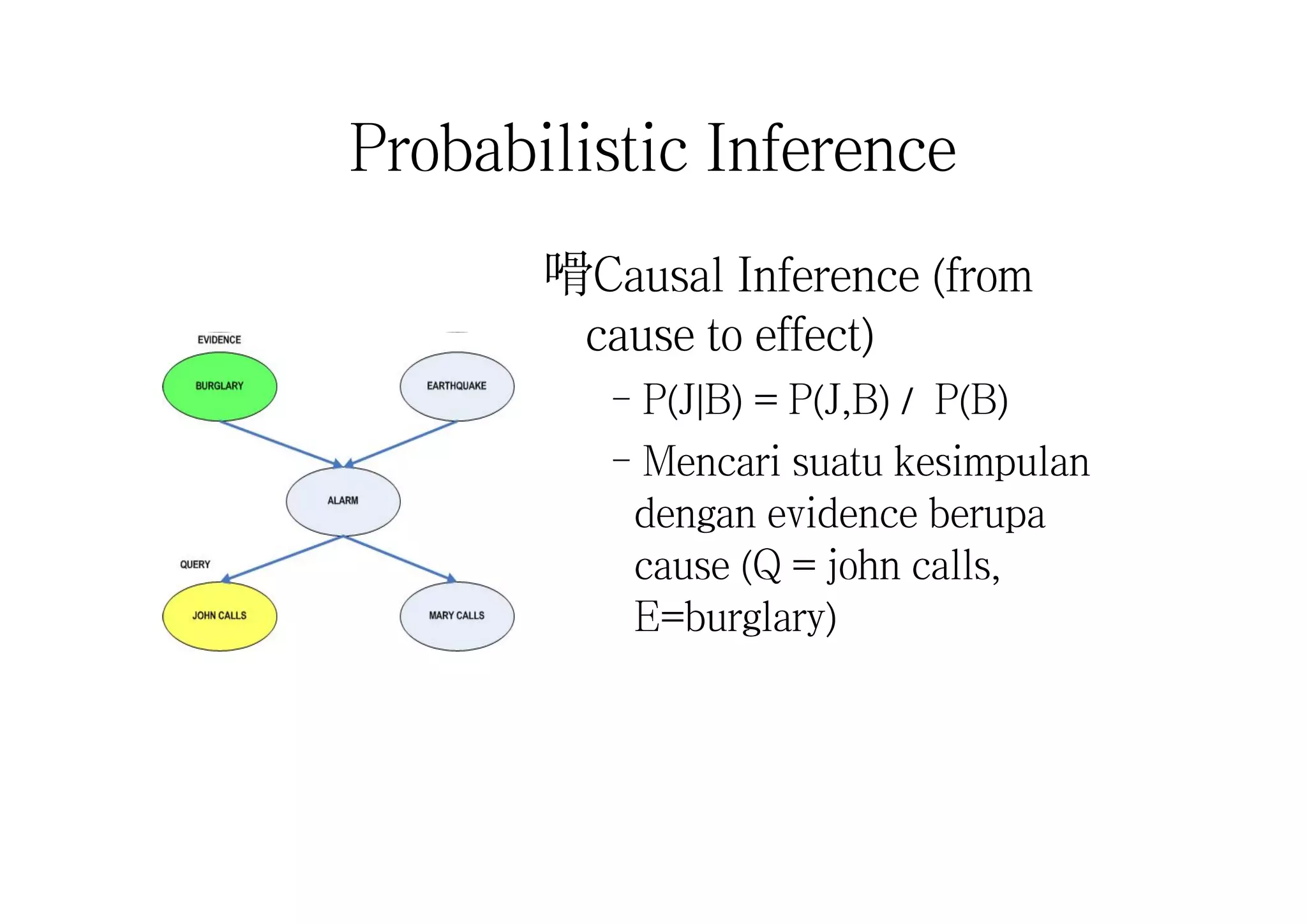
This document discusses machine learning using Bayesian belief networks. It begins by reviewing Bayesian reasoning as a probabilistic approach. It then discusses Bayesian learning as a method used in machine learning that explicitly calculates probabilities for hypotheses. Finally, it provides an example of using Bayes' theorem to calculate probabilities based on prior probabilities and observed data.

1. Machine Learning
Bayesian Belief Network
Oleh :
嗗 Aldy Rialdy Atmadja (23512031)
嗗 Arif Syamsudin (23512099)
嗗 Taufiq Iqbal Ramdhani (23512062)
嗗 Mahar Faiqurahman (23512028)
嗗 Hendri Karisma (23512060)
嗗 Jupriyadi (23512029)

2. Review Bayes
嗗Metodologi Bayesian reasoning
嗗Pendekatan probabilistik untuk menghasilkan inferensi.
嗗Quantity of interest -> Distribusi probabilitas.
嗗Pemilihan yang optimal -> Reasoning (Probabilitas dan observasi data).
嗗Pendekatan kuantitatif, menimbang bukti yang mendukung alternatif hipotesis.

3. Bayesian Learning
嗗Bayesian Learning merupakan suatu metode
pembelajaran yang dikenal dalam machine learning.
嗗Dua alasan bayesian learning dipelajari dalam
machine learning yakni :
–Bayesian Learning menghitung secara eksplisit
probabilitas untuk setiap hipotesis, seperti klasifikasi
pada Naive Bayes.
–Bayesian Learning memberikan perspektif dalam
memahami algoritma pembelajaran lainnya

4. Teorema Bayes
Teorema Bayes menyediakan cara untuk menghitung
probabilitas dari suatu hipotesis berdasarkan probabilitas
sebelumnya, probabilitas mengamati berbagai data yang
diberikan hipotesis, dan data yang diamati itu sendiri.

5. Penggunaan Teorema Bayess
B
G
S
SC
S
P(B)
P(G)
P(S|B)
SC
P(SC|B)
P(SC|G)
P(S|G)
P(SnB) => P(B).P(S|B)
P(ScnB) => P(B).P(Sc|B)
P(SnG) => P(G).P(S|G)
P(ScnG) => P(G).P(Sc|G)
嗗P(B) = Boys
嗗P(G) = Girls
嗗P(S) = Soccer

6. Penggunaan Teorema Bayess
B
G
S
SC
S
0.40
0.60
0.30
SC
0.70
0.60
0.40
P(SnB) = 0.12
P(ScnB) = 0.28
P(SnG) = 0.24
P(ScnG) = 0.36
P(B) = 0.40
P(G) = 0.60
P(S|B) = 0.30
P(S|G) = 0.40
Possibility of Girls Playing Soccer ?
P(G|S) = ???

7. Kemampuan Bayesian Method
Menangani data set yang tidak lengkap.
Pembelajaran mengenai Causal Networks
Memfasiitasi kombinasi dari domain knowledge
dan data.
Efisien dan mempunyai prinsip untuk
menghindari overfitting data.

8. Bayes Optimal Classifier
Klasifikasi ini diperoleh dengan menggabungkan
prediksi dari semua hipotesis

9. Naive Bayes Classifier
Klasifikasi ini diperoleh dengan probabilitas
conditional independence.

10. Naive Bayes Classifier
嗗Keuntungan
–Mudah diimplementasikan.
–Hasil yang baik bila diimplementasikan pada beberapa
kondisi.
嗗Kekurangan
–Asumsi : Conditional independence, loss acuracy.
–Tidak dapat memodelkan dependensi atribut.
嗗Untuk menjawab kekurangan pada Naive Bayes ini digunakan
Bayes Belief Network.

11. Intro Bayes Belief Network
Naive Bayes didasarkan pada asumsi conditional
independence (berdiri sendiri).
Bayesian Network (tractable method) untuk
menentukan ketergantungan antar variabel.

12. Objective & Motivation
嗗Objective: Explain the concept of Bayesian Network.
嗗Reference: www.cse.ust.hk/bnbook
Predisposing factors symptoms test result
diseases treatment outcome.
Class label for thousands of superpixels.

13. Outline
1.Probabilistic Modeling with Joint Distribution
2.Conditional Independence
3.Bayesian Networks
4.Manual Construction of Bayesian Networks
5.Inference
6.Some example

14. The Probabilistic Approach to
Reasoning Under Certainty
嗗Domain Variable: X1, X2, X3, …, Xn
嗗Knowledge about the problem domain is
represented by a Joint Probability P(X1, X2, X3, …,
Xn)

15. The Probabilistic Approach to
Reasoning Under Certainty
Example : Alarm (Pearl 1988)
嗗hnCalls (J), MaryCalls (M)
嗗Knowledge required by the probabilistic approach in
order to solve this problem: P(B,E,A,J,M)
嗗Problem: Estimate the probability of a burglary
based who has or has not called.
嗗Variables: Burglary (B), Earthquake (E), Alaram (A),
JohnCalls (J), MaryCalls (M)
嗗Knowledge required by the probabilistic approach in
order to solve this problem: P(B,E,A,J,M)

16. Join Probability Distribution (JPD)

17. Inference with Joint Probability
Distribution
± What is probability of Burglary given that Mary
Called, P(B=y|M=y)?
± Steps:
1.Compute Marginal Probability
2.Compute answer (reasoning by conditioning):

18. Outline
1.Probabilistic Modeling with Joint Distribution
2.Conditional Independence
3.Bayesian Networks
4.Manual Construction of Bayesian Networks
5.Inference
6.Some example

19. Conditional Independence

20. Conditional Probability Tables
(CPT)

21. Conditional Probability Tables
(CPT)

22. Conditional Probability Tables
(CPT)

23. Outline
1.Probabilistic Modeling with Joint Distribution
2.Conditional Independence
3.Bayesian Networks
4.Manual Construction of Bayesian Networks
5.Inference
6.Some example

24. Bayesian Network
嗗 Each node represent a
random variable
嗗 Between nodes as influences
Recall in introduction
嗗 Bayesian Networks are
networks of random variables.
嗗 The topology of network
determines the relationship
between attributes

25. Independence
Burglary and Earthquake are
independent
P(B,E) = P(B)P(E)
P(B|E) = P(B)
P(E|B) = P(E)
P(B|E) = P(E|B)P(B) = P(B)P(E)
P(E|B) = P(B|E)P(E) = P(E)P(B)

26. Conditional Independent
MeryCalls is
independent of
Burglary dan Earthquake
Given Alarm.
P(M|B,E,A) = P(M|A)

27. Dependent Vs Independent
嗗JohnCalls dan MeryCalls are
Dependent
嗗JohnCalss is Independent of
MeryCalss given Alarm
嗗Burglary and Earthquake are
Independent
嗗Burglary is dependent of
Earthquake given Alarm

28. Causal Independence
嗗Burglary causes
Alarm if motion
sensor clear
嗗Earthquake causes
Alarm iff wire loose
嗗Enabling factors are
independent of each
other

29. Bayesian network topology
Serial Connection
嗗C depend on B, and B depend on
A
嗗If the value of B is known, then A
should be independent from C
(then A d-separated with C)
Divergen Connection
嗗B, C, D.., F depend on A
嗗if the value of A is known, B, C,
D,..F should be independent each
others (d-separated)
嗗otherwise B, C, D,.. dependent

30. Bayesian network topology
Convergen Connection
嗗A depend on B, C, D,,... F
嗗if value of A is unknown, then B, C,
E, ... F should be independent
each others (d-separated)
嗗Otherwise B,C,E,...F dependent
each others

31. Outline
1.Probabilistic Modeling with Joint Distribution
2.Conditional Independence
3.Bayesian Networks
4.Manual Construction of Bayesian Networks
5.Inference
6.Some example

32. Outline
1.Probabilistic Modeling with Joint Distribution
2.Conditional Independence
3.Bayesian Networks
4.Manual Construction of Bayesian Networks
5.Inference
6.Some example

33. Bayesian Network Building
(A)
(B)
Expert
13 Nopember 2012

34. Bayesian Network Building
Komponen Bayesian Network
嗗Kualitatif → Berupa directed acyclic graph (DAG)
dimana atribut direpresentasikan oleh node sedangkan
edge menggambarkan kausalitas antar node
嗗Kuantitatif → Berupa Conditional Probabilitas Table
(CPT) yang memberikan informasi besarnya probabilitas
untuk setiap nilai atribut berdasarkan parent dari atribut
bersangkutan
13 Nopember 2012

35. Excercise Diet
Heart
Disease
Heartburn
Chest PainBlood
Pressure
HD = Yes
E = Yes
D = Healthy
0,25
E = Yes
D = Unhealthy
0,45
E = No
D = Healthy
0,55
E = No
D = Unhealthy
0,75
CP =
Yes
HD = Yes
Hb = Yes
0,8
HD = Yes
Hb = No
0,5
D = No
Hb = Yes
0,4
HD = Yes
Hb = No
0,1
Hb = Yes
D = Healthy 0,8
D =
Unhealthy
0,85
Hb = Yes
HD = Yes 0,85
HD = No 0,2
E = Yes
0,7
D = Healthy
0,25
13 Nopember 2012
Contoh Bayesian Network

36. Tahapan yang dilakukan:
嗗Konstruksi struktur atau tahap kualitatif, yaitu
mencari keterhubungan antara variabel-variabel yang
dimodelkan
嗗Estimasi parameter atau tahap kuantitatif, yaitu
menghitung nilai-nilai probabilitas
13 Nopember 2012
Bayesian Network Building

37. Bayesian Network Building
Ada dua pendekatan yang digunakan untuk mengkonstruksi
struktur Bayesian Network yaitu
1.Metode Search and Scoring (Scored Based)
Menggunakan metode pencarian untuk mendapatkan struktur yang
cocok dengan data, di mana proses konstruksi dilakukan secara iteratif
2. Metode Dependency Analysis (Constraint Based)
Mengidentifikasi/menganalisa hubungan bebas bersyarat (conditional
independence test) atau disebut juga CI-test antar atribut, dimana CI
menjadi “constraint” dalam membangun struktur Bayesian Network.
13 Nopember 2012

38. Algoritma BN building
嗗Search & Scoring Based (Chow-Liu Tree
Construction, K2, Kutato, Benedict, CB, dll)
嗗Dependency Analysis Based ( TPDA, Boundary
DAG, SRA, SGS, PC, dll)
13 Nopember 2012
Bayesian Network Building

39. MMutual Information
Mutual Information
MI dari dua variabel acak merupakan nilai ukur yang
menyatakan keterikatan/ketergantungan (mutual
dependence) antara kedua variabel tersebut.
13 Nopember 2012
Bayesian Network Building

40. (1)
(2)
(3)
(4)
13 Nopember 2012
Bayesian Network Building
Persamaan yang digunakan
Log2

41. (5)
13 Nopember 2012
Bayesian Network Building

42. Tabel data rekam medik
13 Nopember 2012
Bayesian Network Building
Case study

43. 13 Nopember 2012
Teknik Pembobotan
Bayesian Network Building

44. 13 Nopember 2012
Teknik Pembobotan (cont’d)
Bayesian Network Building

45. Tabel hasil pembobotan data rekam medik
13 Nopember 2012
Bayesian Network Building

46. Tabel hasil perhitungan Mutual Information
(3) (4)
(2) (1)
13 Nopember 2012
Bayesian Network Building

47. Tabel hasil perhitungan prob. Dependency 2 node
(5)
(5)
13 Nopember 2012
Bayesian Network Building

48. Contoh struktur network yang terbentuk
13 Nopember 2012
Bayesian Network Building

49. Contoh Tabel Conditional probability yang terbentuk
13 Nopember 2012
Bayesian Network Building

50. Gradient ascent training
嗗Mirip seperti neural networks
–Asumsi bahwa setiap entry dalam CPT adalah sebuah wight
–Bentuk gradient dalam likelihooda, P(D|h), with respect to
the weight.
–Update weights in the direction of the gradient

51. Gradient ascent training

52. Gradient ascent training
嗗Let wijk denote one entry in the conditional probability
table for variable Yi in the network
wijk = P(Yi = yij |Parents(Yi ) = the list uik of values)
e.g., if Yi = Campfire, then uik might be (Storm = T, BusTourGroup = F)
嗗Perform gradient ascent by repeatedly
1.update all wijk using training data D
1.then, renormalize the wijk to assure

54. Outline
1.Probabilistic Modeling with Joint Distribution
2.Conditional Independence
3.Bayesian Networks
4.Manual Construction of Bayesian Networks
5.Inference
6.Some example

55. Inference
嗗Suatu metode yang ada dalam bayesian
network yang digunakan untuk mengambil
suatu keputusan
嗗Inferensi berangkat dari suatu target variabel
jika diketahui variabel yang lain (observed
variable)
嗗P(A | X) - dimana A adalah target variabel
(question), dan X adalah observed variable
(evidence)

56. Inference (cont'd)
嗗Suatu relasi antar atribut (question and
evidence) dapat berupa dependent atau
conditionaly independent

57. Inference
嗗Probabilistic inference
嗗Exact inference
嗗Approximate inference

58. Inference dalam Bayesian Network
嗗Probabilistic Inference
–Diagnostic inference
–Causal inference
–Inter-causal inference
–Mixed inference
嗗Exact inference
–Inference by enumeration
–Variable elemination algorithm
嗗Approximate inference - digunakan apabila terdapat
unobserved variable

59. Probabilistic Inference
嗗Suatu proses untuk mencari / menghitung nilai
dari distribusi probabilitas posterior jika
diketahui beberapa evidence yang ada
嗗Evidence yang diketahui dapat berupa
dependent atribute, maupun conditional
dependent attribute

60. Probabilistic Inference
嗗Diagnostic Inference
(from effect to cause)
–P(B|J) = P(J, B) / P(J)
–Mencari suatu
kesimpulan dimana
evidence yang diberikan
berupa effect
(Q=burglary, E=john
calls)

61. Probabilistic Inference
嗗Causal Inference (from
cause to effect)
–P(J|B) = P(J,B) / P(B)
–Mencari suatu kesimpulan
dengan evidence berupa
cause (Q = john calls,
E=burglary)

62. Probabilistic Inference
嗗Inter-causal Inference
(between causes of the
common effect)
–Contoh: P(B|A) =
P(B,A)/P(A)
–Karena A dependent
terhadap B dan E,
maka P(B,A) =
P(B,A,E) + P(B,A,E')

63. Probabilistic Inference
嗗Mixed Inference
(combining causes and
effects)
–merupakan kombinasi
antara inferensi model
diagnostic dan inferensi
model causal
–contoh: P(A|E,M)

64. 嗗Inference by Enumeration
–Untuk menghitung nilai dari probabilitas dari variable Q
dengan evidence E (E1, E2,...Ek) dapat menggunakan aturan
conditional independentPersamaan tersebut dapat dihitung
dengan dengan menjumlahkan
– persamaan dari full joint distribution
Exact Inference

65. Exact Inference
嗗Inference by Enumeration (cont'd)

66. Exact Inference
嗗Variable Elemination Algorithm

67. Exact Inference
The Algorithm

68. Approximate inference
嗗Digunakan apabila terdapat atribut yang unobserved
嗗Beberapa metode digunakan
–Direct sampling
–Markov chain monte carlo sampling

69. TERIMA KASIH