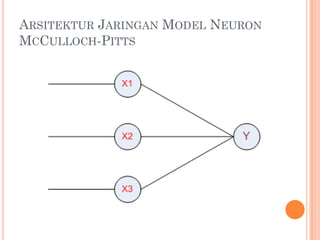
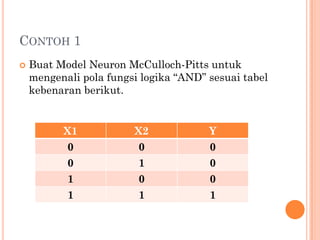
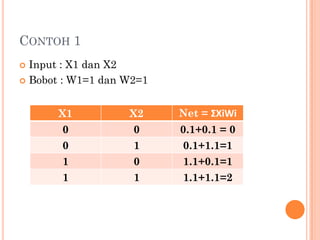
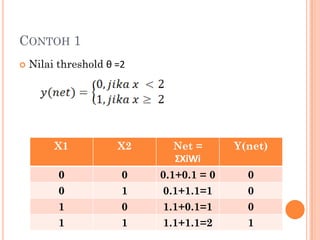
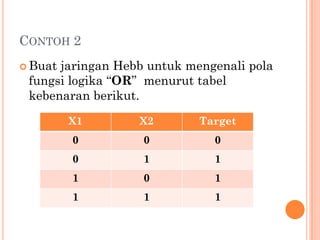
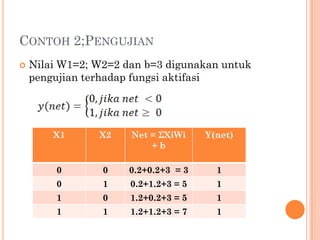
Dokumen tersebut membahas dua model neuron yaitu McCulloch-Pitts dan Hebb. McCulloch-Pitts adalah model neuron pertama yang dirancang tahun 1943, sedangkan model Hebb dirancang tahun 1949 oleh Donald Hebb. Kedua model dijelaskan arsitektur dan algoritmanya beserta contoh penerapan untuk mengenali pola logika AND dan OR.

1. ALGORITMA NEURON
MCCULLOCH-PITTS DAN
NEURON HEBB
Sherly Christina, S.Kom., M.Kom

2. MODEL NEURON MCCULLOCH-PITTS
 Tahun 1943 oleh Warren Mc Culloch, Ahli
Syaraf dan Walter Pitts, Ahli Logika
 Neuron McCulloch-Pitts model JST
pertama

3. ARSITEKTUR JARINGAN MODEL NEURON
MCCULLOCH-PITTS

4. FUNGSI AKTIVASI NEURON MCCULLOCH-
PITTS
 Fungsi Undak Biner

5. CONTOH 1
 Buat Model Neuron McCulloch-Pitts untuk
mengenali pola fungsi logika “AND” sesuai tabel
kebenaran berikut.
X1 X2 Y
0 0 0
0 1 0
1 0 0
1 1 1

6. CONTOH 1
 Input : X1 dan X2
 Bobot : W1=1 dan W2=1
X1 X2 Net = ΣXiWi
0 0 0.1+0.1 = 0
0 1 0.1+1.1=1
1 0 1.1+0.1=1
1 1 1.1+1.1=2

7. CONTOH 1
 Nilai threshold θ =2
X1 X2 Net =
ΣXiWi
Y(net)
0 0 0.1+0.1 = 0 0
0 1 0.1+1.1=1 0
1 0 1.1+0.1=1 0
1 1 1.1+1.1=2 1

8. MODEL NEURON HEBB
1949, D.O. Hebb
Bobot dan Bias dihitung
secara iteratif

9. ARSITEKTUR JARINGAN MODEL
NEURON HEBB

10. ALGORITMA PELATIHAN HEBB
1. Inisialisasi Bobot dan Bias: Wi=0; b=0
2. Untuk setiap pasangan input-target,
lakukan
a. Set aktivasi unit input: Xi=Si; (i=1,2,...,n)
b. Set aktivasi unit output:Yj=tj; (j=1,2,...,m)

11. ALGORITMA PELATIHAN HEBB
3. Perbaiki bobot menurut persamaan
berikut Wi(baru)=Wi(lama)+Xi*Yj;
4. Perbaiki bias menurut persamaan
berikut
b(baru)=b(lama)+Y

12. CONTOH 2
 Buat jaringan Hebb untuk mengenali pola
fungsi logika “OR” menurut tabel
kebenaran berikut.
X1 X2 Target
0 0 0
0 1 1
1 0 1
1 1 1

13. CONTOH 2
Inisialisasi bobot dan bias:
 W1=0
 W2=0
 b=0

14. CONTOH 2; DATA KE-1
 X1 = 0; X2 = 0 ; y= 0 (target)
 Perubahan bobot dan bias untuk data ke-1:
 W1(baru) = W1(lama)+X1*Y
= 0+0.0 = 0
 W2(baru) = W2(lama)+X2*Y
= 0+0.0 = 0
 b(baru) = b(lama)+Y
= 0+0 = 0

15. CONTOH 2; DATA KE-2
 X1 = 0; X2 = 1 ; y= 1 (target)
 Perubahan bobot dan bias untuk data ke-2:
 W1(baru) = W1(lama)+X1*Y
= 0+0.1 = 0
 W2(baru) = W2(lama)+X2*Y
= 0+1.1 = 1
 b(baru) = b(lama)+Y
= 0+1 = 1

16. CONTOH 2; DATA KE-3
 X1 = 1; X2 = 0 ; y= 1 (target)
 Perubahan bobot dan bias untuk data ke-3:
 W1(baru) = W1(lama)+X1*Y
= 0+1.1 = 1
 W2(baru) = W2(lama)+X2*Y
= 1+0.1 = 1
 b(baru) = b(lama)+Y
= 1+1 = 2

17. CONTOH 2; DATA KE-4
 X1 = 1; X2 = 1 ; y= 1 (target)
 Perubahan bobot dan bias untuk data ke-4:
 W1(baru) = W1(lama)+X1*Y
= 1+1.1 = 2
 W2(baru) = W2(lama)+X2*Y
= 1+1.1 = 2
 b(baru) = b(lama)+Y
= 2+1 = 3

18. CONTOH 2;PENGUJIAN
 Nilai W1=2; W2=2 dan b=3 digunakan untuk
pengujian terhadap fungsi aktifasi
X1 X2 Net = ΣXiWi
+ b
Y(net)
0 0 0.2+0.2+3 = 3 1
0 1 0.2+1.2+3 = 5 1
1 0 1.2+0.2+3 = 5 1
1 1 1.2+1.2+3 = 7 1

19. CONTOH 2; HASIL
≠
Y(net) ≠ Target
 JST tidak dapat mengenali pola pada fungsi
logika OR dengan input-output berupa bilangan
biner.

20. TUGAS MANDIRI
 Coba jaringan Hebb untuk mengenali pola
fungsi logika OR dengan ketentuan:
 Input bilangan biner, output bilangan bipolar
 Input bilangan bipolar, output bilangan
bipolar
 Coba jaringan Hebb untuk mengenali pola
fungsi logika AND dengan ketentuan
 Input bilangan biner, output bilangan biner
 Input bilangan biner, output bilangan bipolar
 Input bilangan bipolar, output bilangan
bipolar

21. ADA PERTANYAAN ??
TERIMA KASIH.