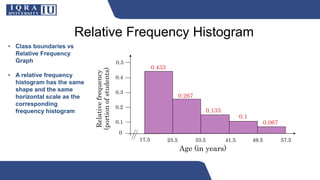
This document discusses frequency distributions and graphical representations of data. It provides the following key points: 1. A frequency distribution table organizes data into classes with frequencies showing how many data points fall into each class. It includes the class limits, frequencies, class marks, relative frequencies, and cumulative frequencies. 2. Graphical representations of frequency distributions include the frequency histogram, frequency polygon, relative frequency histogram, and cumulative frequency ogive. These graphs provide visual analysis of the distribution of data. 3. An example constructs a frequency distribution for ages of participants with five classes and calculates the relevant values like class width, frequencies, class marks, relative frequencies, and cumulative frequencies.

2. Probability and Statistics
Unit 02

3. Learning Outcomes
• Unit 2.1
• Construct a frequency distribution table with classes,
frequencies, class marks, relative frequencies, and cumulative
frequencies.
• Construct frequency histogram, frequency polygon, relative
frequency histogram and o-give.

4. Frequency Distributions
A frequency distribution table represents classes or intervals of data with a frequency
of each class. The frequency of each class is the number of data points exists in that
particular class.
Class Frequency, f
10 – 13 25
14 – 18 13
18 – 22 12
22 – 26 9
26 – 30 4
Frequencies
Lower
Class
Limits

5. Frequency Distributions
The class width is the difference between two consecutive lower limits or two con
secutive upper limits
The range is the difference between the maximum and minimum values
Class Width = 4
Range = 30 – 10 = 20
Class Frequency, f
10 – 13 25
14 – 18 13
18 – 22 12
22 – 26 9
26 – 30 4
14 – 10 = 4
18 – 14 = 4
22 – 18 = 4
26 – 22 = 4

6. Frequency Distribution
Example:
The following data represents the ages of 30 participants in a Workshop.
Construct a frequency distribution that has five classes.
34 19 32 19 30 19
29 18 21 27 20 20
33 30 32 44 39 46
21 54 18 51 49 21
38 24 18 37 29 22
The Example in this slide is adapted from Elementary Statistics: Picturing
the World – Larson and Farber – 3e

7. Frequency Distribution
Example Cont.
No of Classes: 5
Minimum Value = 18
Maximum Value = 54
Range = Max. Value – Min Value
Range = 54 – 18 = 36
Class Width =
34 19 32 19 30 19
29 18 21 27 20 20
33 30 32 44 39 46
21 54 18 51 49 21
38 24 18 37 29 22
Range
Number of Classes
36
5
= = 7.2 => Round up to 8

8. Frequency Distribution
Example Cont.
• The Class Width is calculated as 8
• The lower class limits are 18, 26, 34, 42, and 50
• The upper class limits are 25, 33, 41, 49, and 57
• Make a tally mark for each data entry in the appropriate class
• The number of tally marks for a class is the frequency for that class.

9. Frequency Distribution
Example Cont.
2
50 – 57
3
42 – 49
4
34 – 41
8
26 – 33
13
18 – 25
Tally Frequency, f
Class
30
f
 
Ages of Students

10. Frequency Distribution
53.5
45.5
37.5
29.5
21.5
50 – 57
42 – 49
34 – 41
26 – 33
2
3
4
8
13
18 – 25
Frequency, f
Class
30
f
 
Class Mark
43  2 = 21.5
18 + 25 = 43
The Class Mark of a class is the midpoint of the class and is obtained by
taking sum of the lower and upper limits of the class divided by two.
(Lower class limit) + (Upper class limit)
2
Class Mark = 18+25
2
Class Mark = 21.5

11. Frequency Distribution
Relative Frequency
The relative frequency of a class is the portion or percentage of the data
that falls in that class and can be obtained by;
Cumulative Frequency
The cumulative frequency of a class is the sum of the frequency for that
class and all the previous classes
Relative frequency =
Class frequency
Sample size
f
n


12. Relative Frequency
50 – 57 2
3
4
8
13
42 – 49
34 – 41
26 – 33
18 – 25
Frequency, f
Class
30
f
 
Relative
Frequency
0.067
0.1
0.133
0.267
0.433 f
n
13
30

0.433

1
f
n
 

13. Cumulative Frequency
30
28
25
21
13
+
+
+
+
50 – 57 2
3
4
8
13
42 – 49
34 – 41
26 – 33
18 – 25
Frequency, f
Class
30
f
 
Cumulative
Frequency
Total number
of students

14. Class Boundaries
49.5  57.5
41.5  49.5
33.5  41.5
25.5  33.5
17.5  25.5
Class
Boundaries
50 – 57 2
3
4
8
13
42 – 49
34 – 41
26 – 33
18 – 25
Frequency, f
Class
30
f
 

15. Unit 2.2
Graphical Representation

16. Frequency Histogram
2
3
4
8
13
Broken axis
Ages of Students
10
8
6
4
2
0
Age (in years)
f
12
14
17.5 25.5 33.5 41.5 49.5 57.5
• Class Boundary vs Frequency Graph
• Bar Graph

17. Frequency Polygon
• Class Marks vs
Frequency Graph
• A frequency polygon
is a line graph that
emphasizes the
continuous change in
frequencies
Broken axis
10
8
6
4
2
0
Age (in years)
f
12
14
13.5 21.5 29.5 37.5 45.5 53.5 61.5
Midpoints
Line is extended
to the x-axis.

18. Relative Frequency Histogram
• Class boundaries vs
Relative Frequency
Graph
• A relative frequency
histogram has the same
shape and the same
horizontal scale as the
corresponding
frequency histogram
0.4
0.3
0.2
0.1
0.5
0
Age (in years)
Relative
frequency
(portion
of
students)
17.5 25.5 33.5 41.5 49.5 57.5
0.433
0.267
0.133
0.1
0.067

19. Cumulative Frequency Graph
• Upper Class boundaries
vs Cumulative
Frequency
• A cumulative frequency
graph or ogive, is a line
graph that displays the
cumulative frequency of
each class at its upper
class boundary
17.5
Age (in years)
Ages of Students
24
18
12
6
30
0
Cumulative
frequency
(portion
of
students)
25.5 33.5 41.5 49.5 57.5
The graph ends
at the upper
boundary of the
last class.

20. Review Questions
• Explain the following:
• Frequency distribution
• Class frequencies
• Class marks
• Relative frequencies
• Cumulative frequencies.

21. Review Question 2

22. Review Question 3