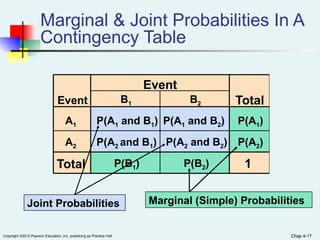
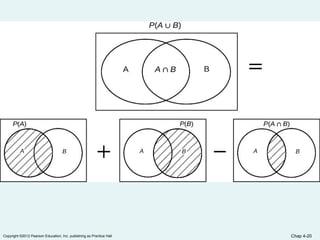
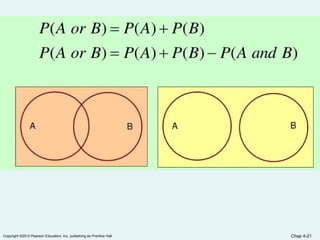
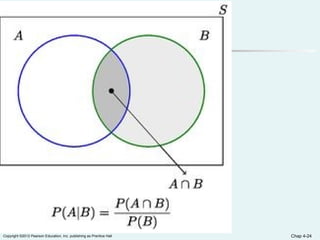
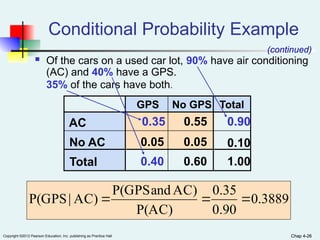
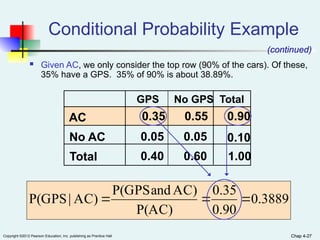
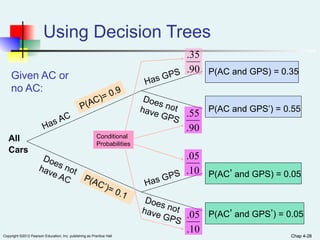
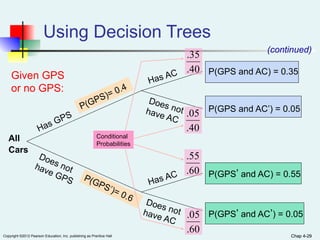
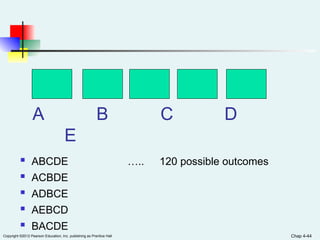
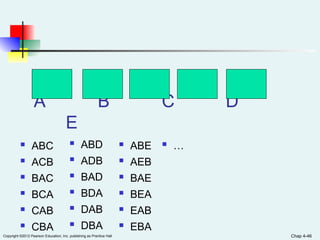
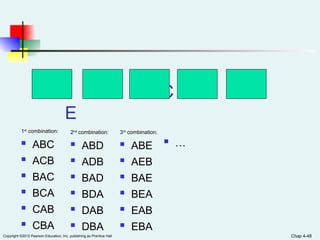
Chapter 4 of the document covers basic probability concepts essential for business statistics, including definitions of probability, types of events, and methods for assessing probabilities. It discusses conditional probability and Bayes' theorem, providing examples to illustrate concepts like joint and marginal probabilities, independent events, and the use of decision trees. The chapter aims to equip readers with the foundational principles of probability necessary for statistical analysis in business contexts.