Downloaded 220 times
Uploaded byFumiya Nozaki
Basic Boundary Conditions in OpenFOAM v2.4
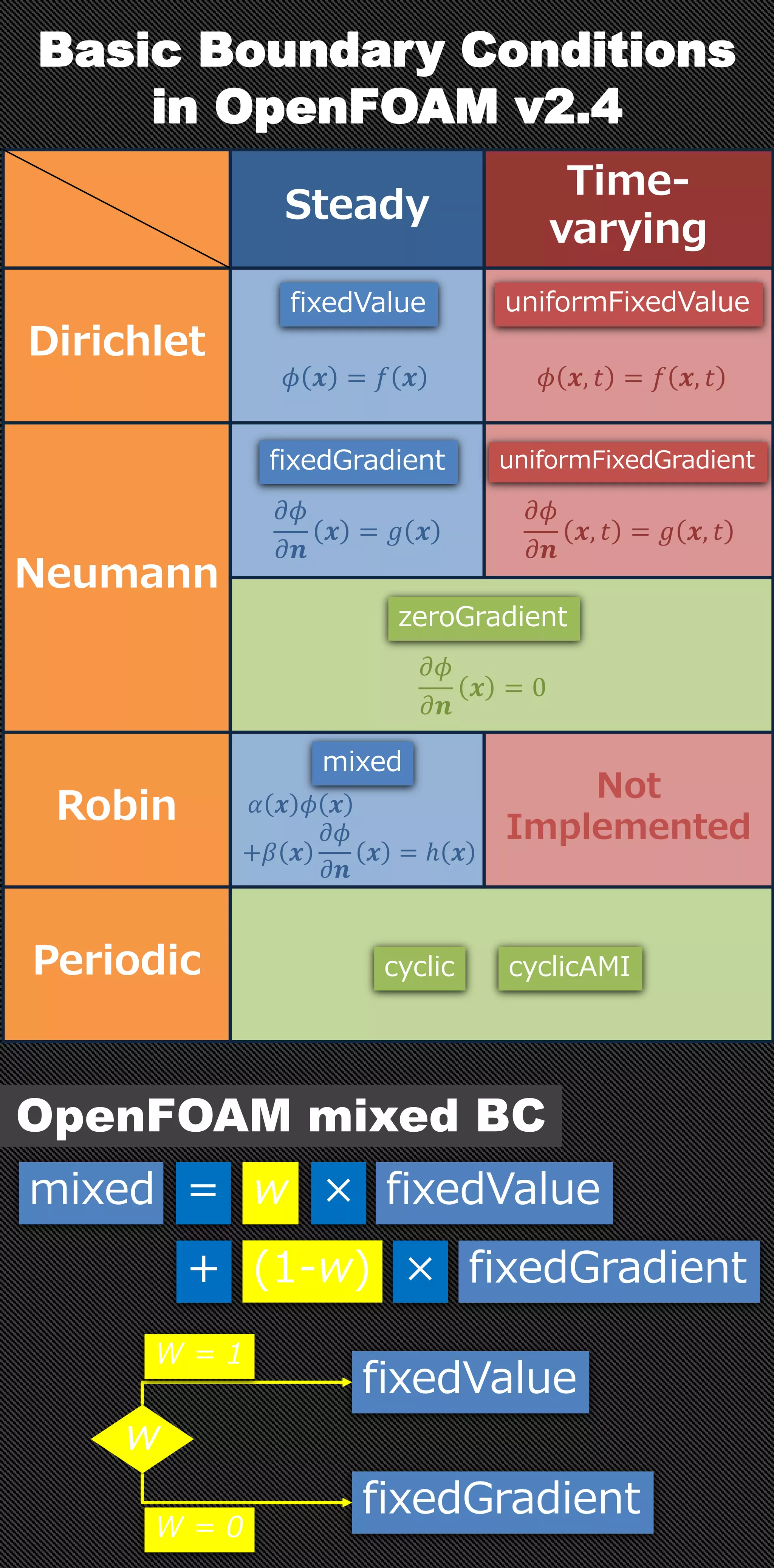
This document discusses different types of boundary conditions in OpenFOAM including: 1) Steady and time-varying boundary conditions such as Dirichlet, Neumann, and Robin conditions. 2) Periodic and symmetry boundary conditions that can be used for repeating geometries. 3) Mixed boundary conditions that are a weighted combination of fixed value and fixed gradient conditions, controlled by a weighting parameter. 4) Direction mixed boundary conditions for vector fields that apply different conditions in different directions using a weighting tensor.
Basic Boundary Conditions in OpenFOAM v2.4
- 1. Basic Boundary Conditions inOpenFOAM v2.4 Classification Steady Time- varying Dirichlet Neumann Robin Not Implemented Periodic Symmetry fixedValue uniformFixedValue fixedGradient uniformFixedGradient zeroGradient mixed cyclic 𝜙 𝒙 = 𝑓 𝒙 𝜙 𝒙, 𝑡 = 𝑓 𝒙, 𝑡 𝜕𝜙 𝜕𝒏 𝒙 = 𝑔 𝒙 𝜕𝜙 𝜕𝒏 𝒙, 𝑡 = 𝑔 𝒙, 𝑡 𝜕𝜙 𝜕𝒏 𝒙 = 0 a𝛼 𝒙 𝜙 𝒙 +𝛽 𝒙 𝜕𝜙 𝜕𝒏 𝒙 = ℎ 𝒙 cyclicAMI mixed BC mixed fixedValue fixedGradient = + × ×w (1-w) w fixedValue fixedGradient W = 1 W = 0 mixed symmetryPlane symmetryPlane or slip? 𝜕𝜙 𝜕𝒏 𝒙 = 0 Scalar 𝜙 Vector 𝝓 𝝓 𝒙 ∙ 𝒏 = 0, 𝜕𝝓 𝑡 𝜕𝒏 𝒙 = 𝟎 symmetryPlane is used on a single and perfectly flat boundary slip can be used on curved boundaries symmetryPlane slip 𝒏 mixed BC is a combination of fixedValue and fixedGradient BCs A weighting parameter w (0-1) switches between these types directionMixed BC For vector fields, directionMixed BC is a combination of fixedValue and fixedGradient BCs A weighting parameter (tensor) controls which direction these BCs are apply to 1 2 𝒏 ⊗ 𝒏 + 𝒏 ⊗ 𝒏 𝑇 w 𝑂3 (Zero matrix) 𝐼3 (Identity matrix) fixedValue fixedGradient fixedGradient fixedValue Normal direction Tangential direction All directions