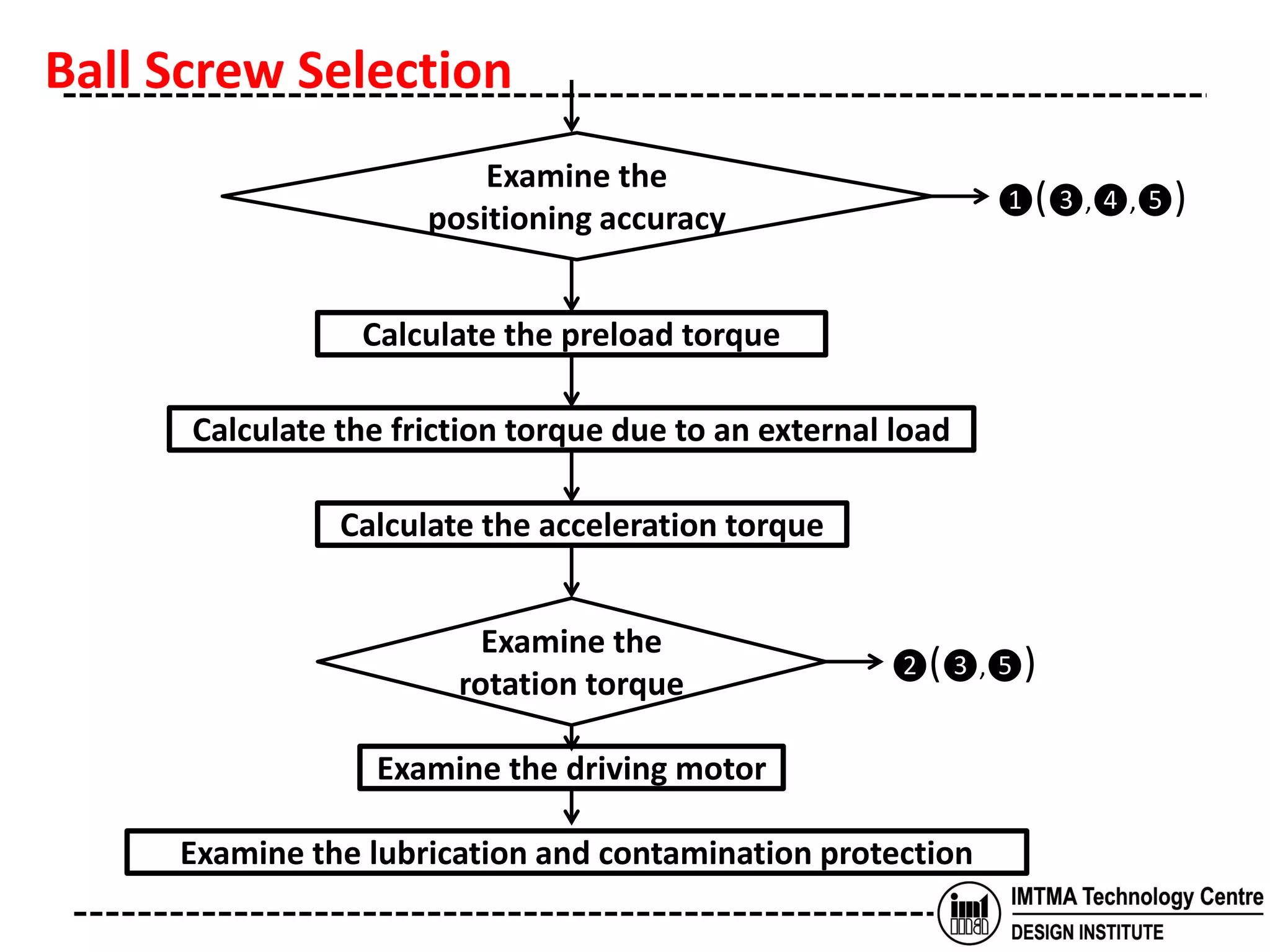
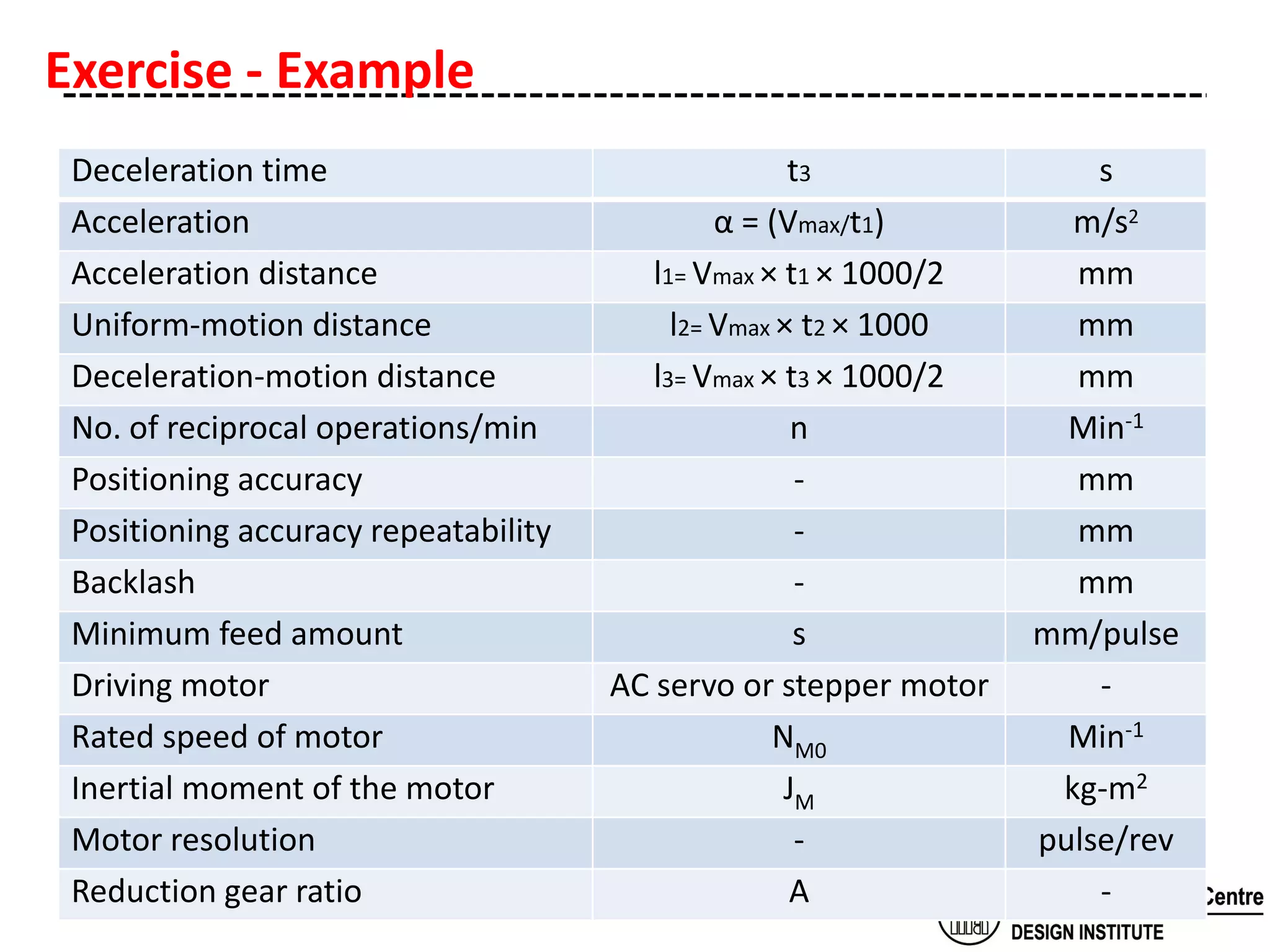
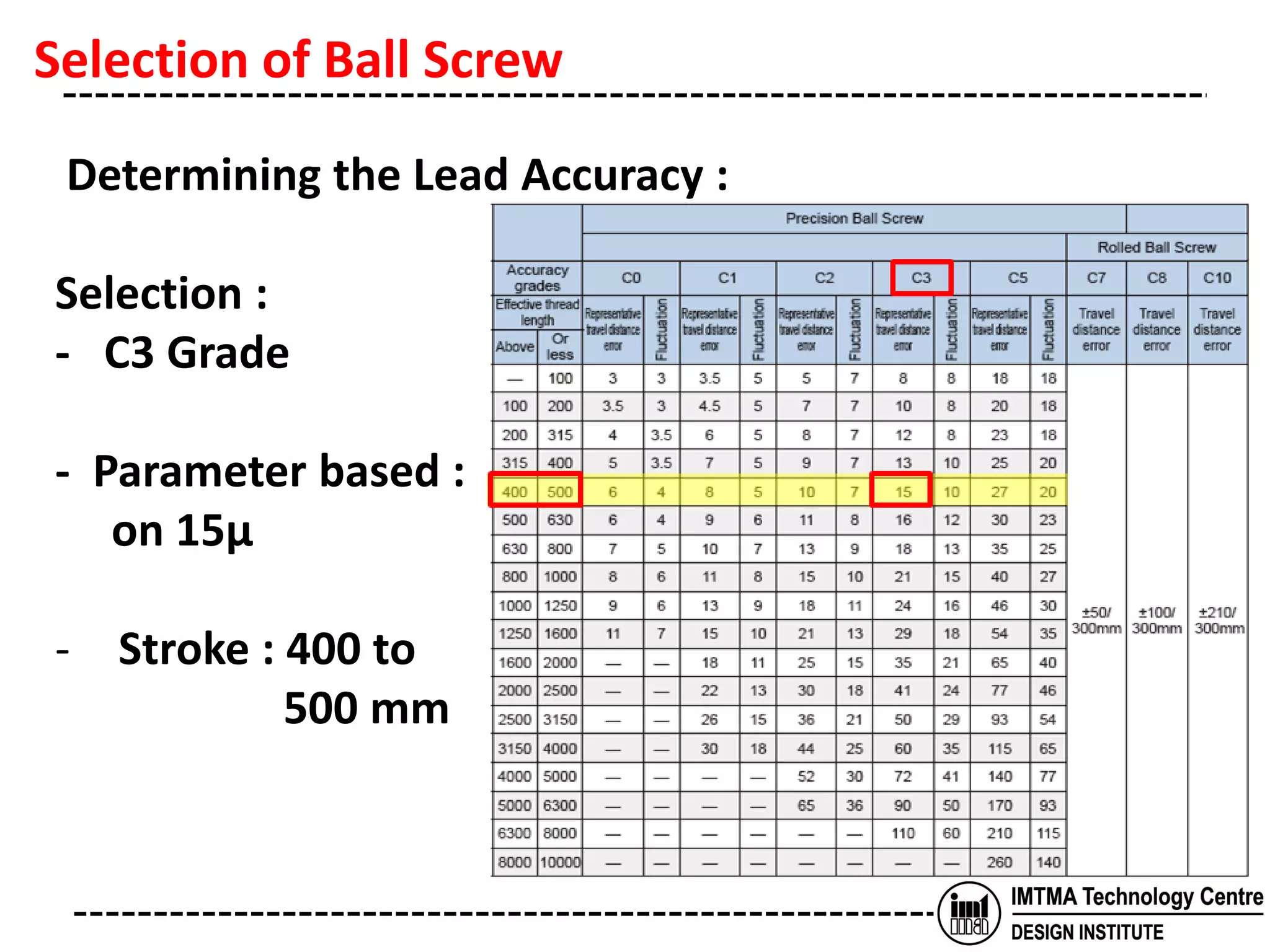
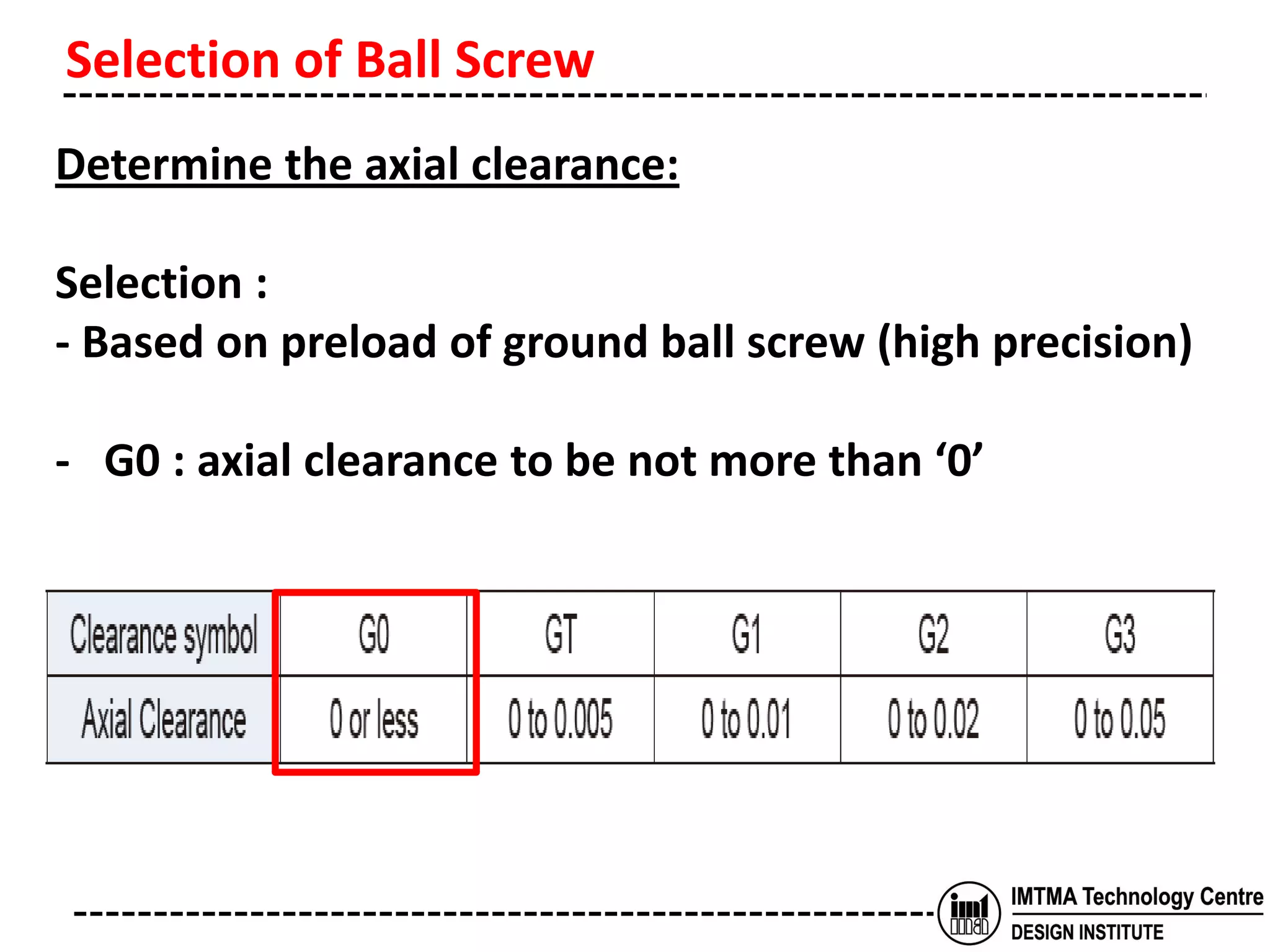
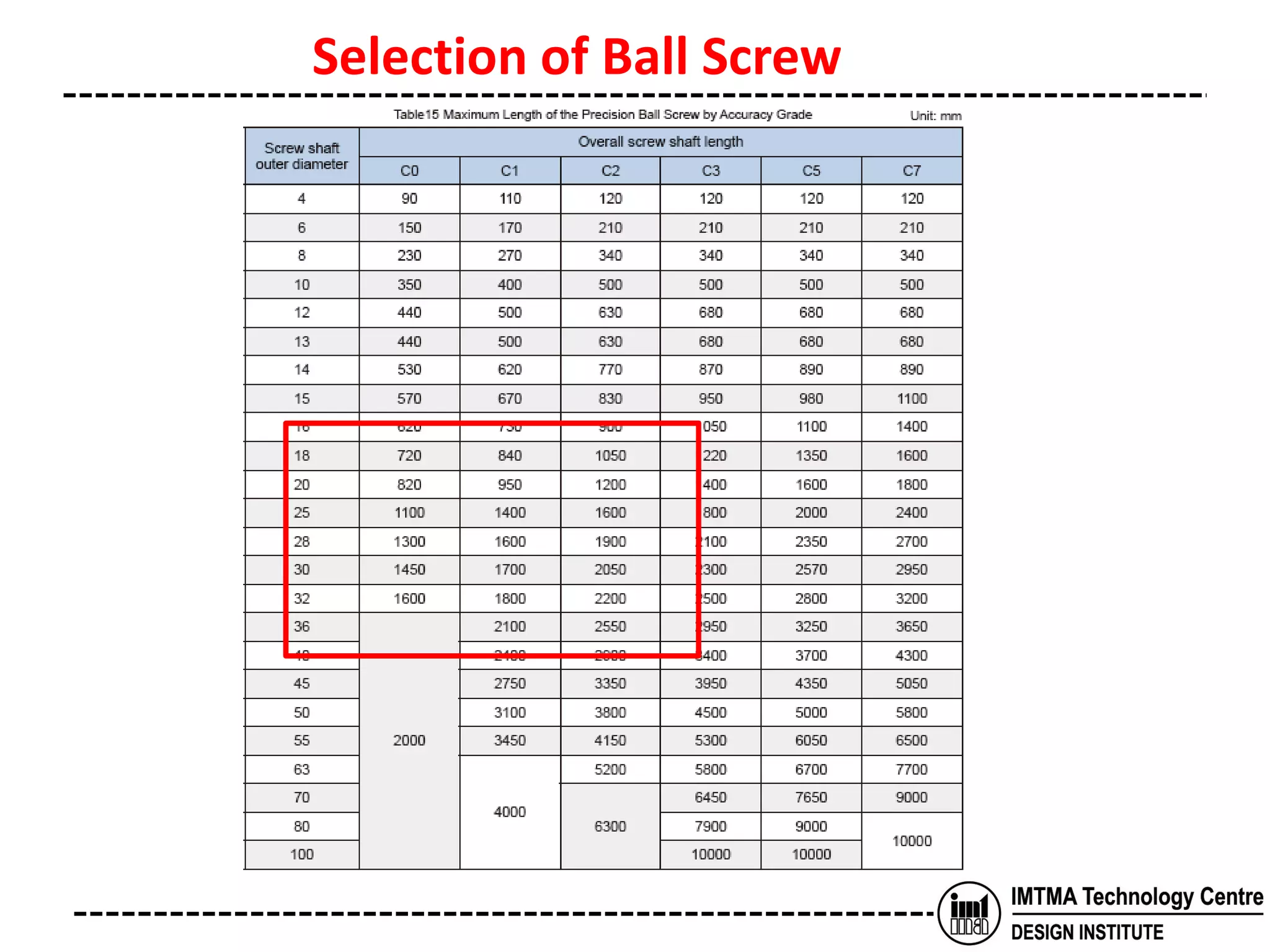
The document discusses the selection of a ball screw for a machine tool based on its operating conditions and design specifications. It outlines the steps to determine the key parameters for the ball screw like lead accuracy, axial clearance, screw length and diameter, support method, permissible axial load and rotational speed, nut model, rigidity, positioning accuracy, torques required, and motor specifications. An example selection process is provided based on the given design data and machine specifications for a lathe machine. Key factors like buckling load, tensile strength and critical speeds are examined to ensure safe design of the ball screw.

1. MACHINE TOOL DESIGN-PROFESSIONAL
1
1/7/2014
TOPIC : BALL SCREW SELECTION
By:
HV RajaShekara
DIRECTOR - Design Institute,
IMTMA

2. BALL SCREW

3. Application

4. Ball Screw Mountings
• Precision angular contact bearings of class P3 is
employed to give high running accuracy.
• Bearings with 60° contact angle is used for high axial
load. (Ex: Metal removal)
• Fixed-Fixed arrangement for high speeds and pre-
stretched to compensate thermal expansion.

5. • The ball screw on the support end is free to expand if
temperature rise is beyond the pre-stretched limit,
hence buckling due to thermal effects is avoided.
• The ball screw and motor assembly are placed
centrally to guideways for minimizing the tilting
moment.
Ball Screw Mountings

6. • Ball screw converts the rotary motion of the servo
motor and imparts linear motion to the slides.
• Tool Requirement :
 Hi – Precision
 Hi – Efficiency
 Less torque
 High axial rigidity
 Zero axial clearance
 Very fine increments
 Fast traverse speeds
Introduction

7. • Ball screw require 1/3 less torque compared to a
conventional sliding screw.
• Easy to convert rotary to linear and vice versa.
• Due to intricacies of the ball screw, its selection
should be very meticulous based on various
calculations.
Introduction

8. Ball Screw Selection
Determining the Operating Conditions
Determine the lead accuracy
❶
Determine the
axial clearance
Precision Ground
Ball Screw (high
precision)
Rolled Ball Screw
(low price)
Assume the shaft length
Determine the lead length
❷
Determine the shaft diameter
❸

9. Ball Screw Selection
Determine the Shaft
support method
❹
Examine the
permissible axial load
❸ (❹)
Determine the
permissible rotational
speed.
❸ (❷,❹)
Determine the Nut model No.
❺

10. Ball Screw Selection
Examine the
permissible axial load
❺(❷,❸)
Examine the Service
Life
❺(❷,❸)
Calculate rigidity in the shaft axial direction
Calculate the nut rigidity
Calculate the support bearing rigidity
Examine the
rigidity ❸(❹❺)

11. Ball Screw Selection
Examine the
positioning accuracy
❶(❸,❹,❺)
Calculate the preload torque
Calculate the friction torque due to an external load
Calculate the acceleration torque
Examine the
rotation torque
❷(❸,❺)
Examine the driving motor
Examine the lubrication and contamination protection

12. Exercise
• Determining the operating conditions:
PARAMETERS SYMBOL UNIT
Transfer orientation horizontal,
vertical,etc
-
Transferred mass m kg
Table guide method sliding, rolling
Frictional coefficient of the guide
surface
µ
Guide surface resistance f N
External load in the axial direction F N
Desired service life time Lh h
Stroke length ls mm
Operating speed Vmax m/s
Acceleration time t1 s
Uniform-motion time t2 s

13. Deceleration time t3 s
Acceleration α = (Vmax/t1) m/s2
Acceleration distance l1= Vmax × t1 × 1000/2 mm
Uniform-motion distance l2= Vmax × t2 × 1000 mm
Deceleration-motion distance l3= Vmax × t3 × 1000/2 mm
No. of reciprocal operations/min n Min-1
Positioning accuracy - mm
Positioning accuracy repeatability - mm
Backlash - mm
Minimum feed amount s mm/pulse
Driving motor AC servo or stepper motor -
Rated speed of motor NM0 Min-1
Inertial moment of the motor JM kg-m2
Motor resolution - pulse/rev
Reduction gear ratio A -
Exercise - Example

14. Machine specification
Swing over Saddle mm 350
Swing over Cross Slide mm 220
Chuck Size mm 165
Distance b/w Centres mm 380
Turning Diameter max. mm 165
Turning Length max. mm 350
Nose A2-5
Bore taper MT-4
Power kW 5.5
Maximum Speed rpm 4000
Speed range at constant power rpm 1000-3500
Spindle Bore mm 40
Standard Bar Capacity mm 26
Stroke X-Axis mm 130
Stroke Z-Axis mm 350
Feed rate mm/min 0-5000
Rapid Traverse Rate m/min 24
Bed slant angle deg 45
MACHINE SPECIFICATION
Machine Capacity
Spindle
Travels & Feedrates

15. Design Data
• Cutting speed Vc = 150m/min
• Maximum velocity Vmax = 24m/min
• Mass of the Z slide assembly m1 = 110kgs
• Mass of the X slide assembly m2 = 27kgs
• Mass of the turret assembly m3 = 42kgs
• Mass m4 = 104kgs
• Stroke Ls = 350mm
• Deceleration time t1 = 0.1 sec
• Acceleration time t2 =0.1 Sec
• Positioning accuracy 0.01/500mm
• Cutting force Px = 440N
• Axial force Pz = 1465N
• Guide resistance f = 29N
• Motor speed n =3000rpm
• Motor Torque Tm = 4.7Nm
• Guide way co-efficient of friction µ = 0.003
• Ratio i = 1:1 ( direct coupling )
• Minimum feed amount s = 0.001mm/p

16. • Mass of the Z-Axis Assembly = 290kgs
• Resistance of the guide way, f = 𝝁 ∗ 𝒎 ∗ 𝒈
= 𝟎. 𝟎𝟏 ∗ 𝟐𝟗𝟎 ∗ 𝟗. 𝟖𝟏 = 𝟐𝟗 𝑵
• Acceleration ‘α’ =
𝑽𝒎𝒂𝒙
𝒕𝟏
=
𝟎.𝟒𝟎
𝟎.𝟏
= 4.0m/s2
Selection of Ball Screw

17. Determining the Lead Accuracy :
Selection :
- C3 Grade
- Parameter based :
on 15µ
- Stroke : 400 to
500 mm
Selection of Ball Screw

18. Determine the axial clearance:
Selection :
- Based on preload of ground ball screw (high precision)
- G0 : axial clearance to be not more than ‘0’
Selection of Ball Screw

19. Determine the overall screw length:
- Overall length of nut (assumed) = 150mm
- End length(assumed) = 200mm
- Stroke length = 350mm
- Overall length of screw shaft = 150+200+350
= 700mm
Selection of Ball Screw

20. Determining the lead:
The rated motor speed of 3000 rpm and a specified
max speed of 400mm/sec requires a ball screw lead:
Lead min = 𝑴𝒂𝒙. 𝒍𝒊𝒏𝒆𝒂𝒓 𝒔𝒑𝒆𝒆𝒅
𝑹𝒂𝒕𝒆𝒅 𝒎𝒐𝒕𝒐𝒓 𝒔𝒑𝒆𝒆𝒅
= 400 × 60
3000
= 8 mm or greater
Select the lead : 10mm
Selection of Ball Screw

21. Encoder Selection:
The Ball Screw and motor are directly coupled without
using a reduction gear, the min resolution is derived
from the resolution of the encoder which is attached to
the AC Servo motor.
To meet the minimum feed of 0.001 mm/pulse the
encoder must generate:
=
𝟏𝟎
𝟎.𝟎𝟎𝟏
= 10000 PPR
Selection of Ball Screw

22. Screw Shaft Diameter:
Lead = 10 mm
For lead of 10mm
Diameter of screw shaft can be of
1. 15mm
2. 20mm
3. 25mm
4. 32mm
From manufacturing point of view, for
C3 class, Greater than 15mm need to selected.
Hence, O.D = 25mm and 32 mm will be selected (tentatively)
Selection of Ball Screw

23. Selection of Ball Screw

24. Supporting Method:
• Max speed - 400mm/sec Fixed – Supported or
• Stroke length - 350mm Fixed – Fixed
However ; Fixed – Fixed
• Positioning accuracy = ± 0.015mm/500mm
Reason: Pretension the Screw shaft to minimize the
effects of temperature rise due to heating.
Selection of Ball Screw

25. Examine the permissible axial load:
• Axial load in accelerating motion (Fa1) :
Fa1 = f + µ.g.m + mα
= 29 + 0.01 × 290 × 9.81 + 290 × 4.0 = 1218 N
• Axial load in constant speed motion (Fa2) :
Fa2 = µ.m.g + f
= 0.01 × 290 × 9.81 + 29 = 57.5 N
• Axial load in decelerating motion (Fa3) :
Fa3 = µ.m.g + f –mα
= 0.01 × 290 × 9.81 + 29 – 290 × 4.0 = -1102.5 N
Selection of Ball Screw

26. Examine the permissible axial load:
• Axial load in light cutting operation(Fa4) :
Fa4 = Cutting force Px (turning) + Fa2
= 450 + 57.5 =1284 N ≈ 507 N
• Axial load in heavy cutting operation (Fa5) :
Fa5 = Cutting force Px(drilling thrust)+ Fa2
= 5400 + 57.5 = 14534 ≈ 5475.5 N
∴ The max axial load acting on Ball Screw
Famax = 5,475.5N
Selection of Ball Screw

27. Examine the Buckling load considerations:
P1 = (ɳ2.d1⁴.10⁴)/Ia2
= (20 × 22.2⁴ × 10⁴) / 4652 ≈ 224665.3 N
Where, ɳ2 - Coeff. Dependent on the mounting
method = 20 (Page – 30)
d1 – Screw shaft root dia = 22.2 mm(page - A15-188)
Ia – mounting distance
= 350 + 75 + 37.5
= 465 mm
Selection of Ball Screw

28. Examine the Buckling load considerations:
Where,d1 – Screw shaft root dia = 22.2 mm(page - A15-188)
Ia – mounting distance
= 350 + 75 + 37.5 = 465 mm
Selection of Ball Screw

29. Allowable Tensile & Compressive load:
P2 = (116.d21)
= (116 × 21.42) ≈ 53123.36 N
∴ P1 & P2 > Famax
Hence, Design is SAFE
Selection of Ball Screw

30. Determine the permissible rotational speed:
• Maximum rotational speed (Nmax) :
Nmax = Vmax / I
Where, I – Lead of screw shaft
= 400/10
= 40 rps
= 2400 rpm
• Critical speed of screw shaft (N1) :
N1 = (λ2.d1.10⁷)/ Ib
2
= (21.9 × 21.4 × 10⁷)/5652
= 14681.2 rpm
Selection of Ball Screw

31. Determine the permissible rotational speed:
• Critical speed of screw shaft (N1) :
N1 = (λ2.d1.10⁷)/ Ib
2
Where, λ2 -Page 32
Ib – Mounting distance
Selection of Ball Screw

32. Determine the permissible rotational speed(N2):
• DN Value N2 = 70000/D
Where, D – ball center to center diameter (page A-15 188)
N2 = 70000/26.3
= 2661.59 rpm
OR
Selection of Ball Screw

33. DN not greater than 70,000 (Condition)
DN = 26.3 × 2400
= 63,120
∴ N2 < Nmax & DN < 70,000
HENCE THE DESIGN IS SAFE
Selection of Ball Screw

34. Exercise
Drive motor: Specification/Requirements
Frictional torque due to external load:
T1 = Fa . l . A / (2.π.ɳ)
Where, Reduction gear ratio ‘A’ = 1
Fa = F + .µFv = 2244 + 0.15 × 180 × 9.81
PARAMETERS SYMBOL VALUE
Vertical load Fv 180
Coefficient of friction b/w guideways µ 0.15
Ball screw effiency ɳ 0.9
Cutting force
(drilling thrust for 0.12 mm feed)
F 2244

35. Exercise
Drive motor: Specification/Requirements
Tp = Fa . l . A / (2.π.ɳ)
= (2508.87 × 10 × 10ˉ3) / (2 × π × 0.9)
= 4.4367 Nm

36. Exercise
Torque due to pre loading of ball screw (Td)
Td = (0.05 (tan β) ˉ0.5 . Fa0 .l. 10ˉ3) /(2.π)
Where,
tan β = lead/(π. Ball center to center diameter)
tan β = 10/(π × 33.75)
= 0.094
Fa0 (Preloading load) = 10% of Ca
= 0.1 × 34.8
= 3.45 kN

37. Exercise
Td = (0.05 (tan β) ˉ0.5 . Fa0 .l. 10ˉ3) /(2.π)
Td = (0.05 (0.094) ˉ0.5 × 3.48 × 10ˉ3 × 10 × 10ˉ3) /(2.π)
Td = 0.903248 Nm
Total torque : Tp + Td
= 4.4367 + 0.9032
= 5.34 Nm

38. Exercise
Rotational speed (Nm) and Resolution (B):
Rotational speed (Nm):
Nm = V / (I.A)
= 15000 / (10 × 1)
= 1500 rpm
Resolution (B):
B = (I.A)/S
Where, S = Min Feed = 0.001mm
= (10 × 1) / 0.001
= 10,000 ppr

39. Exercise
Torque required for acceleration:
TA = J.ω
J = m. (I /(2. π )) 2 .10⁶ + Js + JM + Jc
Where, J – Moment of Inertia
Js – Screw shaft moment of Inertia
= 8.08 × 10ˉ3 kg.m2
For length of 750 mm = 6.06 × 10ˉ4 kg.m2
JM – Moment of inertia of motor = 0.0026 kg.m2
Jc – Moment of inertia of coupling
= 0.000664 kg.m2
M = 180 Kgs

40. Exercise
Torque required for acceleration:
J = m. (I /(2. π )) 2 .10⁶ + Js + JM + Jc
TA = 180 × (10 /(2 × π))2.10⁶ + 6.06 × 10ˉ4 + 0.0026 + 0.000664
= 4.32 × 10ˉ3 kg.m2
ω = (2. π.NM)/(60.t)
= (2 × π × 1500)/(60 × 0.1)
= 1570.79 rad/sec 2
TA = J.ω
TA = 4.32 × 10ˉ3 × 1570.79
= 6.78 Nm

41. Exercise
Moment of inertia (JM):
JM = J/C
Where, C = Coefficient depending on the motor and driver
= 5
= 4.32 × 10ˉ3 / 5
= 8.64 × 10ˉ4 kg.m2
∴ Moment of inertia of the motor should not be less than
8.64 × 10ˉ4 kg.m2

42. Exercise
Selected - 6/2000
• Rated rotational speed not less than 1500 rpm.
• Resolution obtained from the encoder and driver should
be 10,000 ppr.
• Instantaneous maximum torque not less than 6.78Nm.
• Rated torque not less than 5.35Nm.
• Moment of inertia of the motor not less than 8.64×10ˉ4
kg.m2.

43. Exercise
Calculation of rigidity:
Axial rigidity of Screw Shaft (Ks) :
Ks = (4.A.E) / (1000. L)
Where, A = (π × d1
2)/4
= (π × 26.22)/4
= 547.11 mm2
L = Mounting distance = 620 mm
Ks = (4 × 547.11 × 206 ) / (1000× 620)
Ks = 0.727 kN/µm

44. Exercise
Calculation of rigidity:
Axial rigidity of Nut (KN) :
KN = (K .Fao/(0.1.Ca))⅓
Where, KN = K Since , Fao is 10% of Ca
KN = 870 kN/µm
Axial rigidity of Support Bearings (KB) :
KB = 0.655 kN/µm
(From bearing catalogue)

45. Exercise
Calculation of rigidity:
Axial rigidity of Total ball screw system (K) :
(1/K) = (1/ Ks) + (1/ KN) + (1/ KB)
= (1/0.727) + (1/0.87) + (1/0.655)
= 4.05166
K = 0.2468 kN/µm
Lost motion : Due to resistance of guideway
R = (2.Fa1) / K
=(2 × 0.54) / 0.2468
= 2.188µm
(Also depends on motor, coupling, drive elements)

46. Exercise
Thermal displacement due to heat:
3 °C Provided corresponding to Pre tension
+
3 °C Doubt
Δl = - (ƿ.t.l)
= (12 × 10-6 × 3 × 620)
= - 0.02232mm
Pre Tension: Fs = Δl. Ksl
Where, Ksl = Rigidity of thread screw b/w support bearing
= Ks/4

47. Exercise
Thermal displacement due to heat:
Pre Tension: Fs = Δl. Ksl
Where, Ksl = Rigidity of thread screw b/w support bearing
= Ks/4
= 0.727/4
= 0.1875 kN/µm
Fs = Δl. Ksl
= 22.32 × 0.18175
= 4.05 KN

48. Design verification
Ball screw diameter….………30mm
Lead…………………………….12mm
Stroke…………………………..300mm
Rapid speed…………………..30m/min
Acceleration time…t1………..0.15sec
Deceleration time…t2………0.15 sec
Maximum velocity…V……….0.5m/s
Mass of the table…m1…………340kgs
Mass of the work…m2………...150kgs
Motor speed and torque……..3000rpm / 7Nm
Motor inertial moment………..0.012kgm^2
Tangential force…Ft ………..142Kgf
Distance b/w ball screw support …715mm
Data based on standards

49. Design verification
Check for buckling load
1. Acceleration,  = V/t1 = 0.5/0.15 = 3.33m/s^2
2. Axial load, Fa1 = (m1+m2)g + f + (m1+m2) + Ft
= 0.003*(340+150)*9.81+ 50 + (340+150)*3.33 + 1420
= 3120N
3. Screw buckling load = (*d1^4*10^4)/La^2
= (20*26.1^4*10^4)/715^2
= 181550N
4. Screw permissible tensile load = 116*d1^2
= 116*26.1^2
= 79020N
Result Buckling load > Axial load max. and also
Permissible tensile load > Axial load max.
181550N > 3120N & 79020N > 3120N
( HENCE THE DESIGN IS SAFE)

50. Design verification
Maximum rotational speed
1. Maximum screw speed, Nmax. = (V*60*10^3) / l
= (0.6*60*10^3) / 12
= 3000rpm
2. Critical Speed Ncr = (2*d1*10^7) / La^2
= (21.9*26.1*10^7) / 715^2
= 11200rpm
N critical > N max
11200 > 3000
(Hence the design is safe)

51. Design verification
Maximum rotational torque.
1. Frictional torque, T1 = Fa*l*A / (2**)
= (3120*12*1) / (2*3.14*0.9) * 1000
= 6600Nmm
2. Acceleration torque T2 = (J+Jm)*
Angular acceln.  = (2**N) / (60*t1)
= (2*3.14*3000) / (60*0.15)
= 2000rad/sec^2
Screw inertial moment Js = 1.23*10^-3 * 1000*10^-4
= 1.23*10^-4 kgm^2
Mass inertial moment J = (m1+m2) * (l/2/)^2 (*A^2 * 10^-6) + (Js^2 *
A^2)
= (340+150) * (12/2/3.14)^2 * (1^2* 10^-6) +
(1.23*10^-4 * 1^2)
= 0.00193 kgm^2
 Acceleration Torque T2 = (0.00123+0.00193) * 2000 *1000
= 6320Nmm

52. Design verification
Total torque during accln. T = T1+T2
= 6600+6320
= 12920Nmm
Motor torque rated = 7000Nmm
Motor torque peak = 18000Nmm
Hence, Motor torque peak > Total torque during acceleration
18000Nmm>12920Nmm
( Hence the design is safe)
Effective torque value = (Tk^2*t1)+(T1^2*t2)+(tg^2*t3)+(Ts^2*t4)
------------------------------------------------------
(t1+t2+t3+t4)
= 4872Nmm
Hence, Motor rated torque > Effective torque value
7000Nmm > 4872Nmm
( Hence the design is safe)