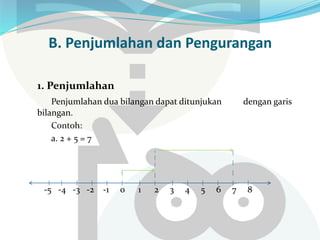
Dokumen ini merupakan materi pelajaran matematika untuk kelas VII dengan fokus pada bilangan bulat, mencakup operasi hitung seperti penjumlahan, pengurangan, perkalian, dan pembagian. Tujuan pembelajaran adalah agar siswa dapat memahami dan menerapkan sifat-sifat bilangan bulat dalam berbagai konteks. Selain itu, dokumen ini juga menjelaskan konsep pemangkatan, akar, dan taksiran dalam bilangan bulat.

1. Oleh
Nama : Meilani Rahmawati
NPM : 1441172105061
Prody : Pendidikan Matematika 3C
Fakultas Keguruan dan Ilmu Pendidikan
Universitas Negeri Singaperbangsa
Karawang
2015

2. MATERI PELAJARAN : MATEMATIKA
KELAS : VII
SEMESTER : GASAL
MATERI POKOK : BILANGAN BULAT
STANDAR KOMPETENSI
Memahami sifat-sifat operasi
hitung bilangan dan
penggunaannya dalam
pemecahan masalah
KOMPETENSI DASAR
1.1 Melakukan operasi hitung
bilangan bulat dan pecahan
TUJUAN PEMBELAJARAN
Setelah pembelajaran ini, siswa diharapkan
dapat :
1. Memberikan Contoh Bilangan Bulat
2. Menyatakan sebuah besaran sehari-hari yang
menggunakan bilangan negatif
3. Menentukan letak bilangan bulat dalam garis
bilangan
4. Menyelesaikan operasi tambah, kurang, kali, bagi
dan pangkat bilangan bulat termasuk operasi
campuran
5. Menentukan sifat-sifat perkalian dan pembagian
bilangan negatif dengan negatif dan positif dengan
negatif
6. Menghitung kuadrat dan pangkat tiga serta akar
kuadrat dan akar pangkat tiga bilangan bulat
7. Memaksimalkan perkalian dan pembagian bilangan
bulat
8. Menemukan dan menggunakan sifat perkalian,
pembagian bilangan bulat untuk menyelesaikan
masalah.

3. BILANGAN BULAT
A. Pengertian Bilangan Bulat
B. Penjumlahan dan Pengurangan Bilangan Bulat
C. Perkalian dan Pembagian Bilangan Bulat
D. Taksiran Pada Bilangan Bulat
E. Pemangkatan dan Akar
F. Akar Kuadrat Bilangan Bulat

4. A. Pengertian Bilangan Bulat
Bilangan 0, 1, 2, 3, 4 … disebut bilangan cacah
Bilangan 1, 2, 3, 4, … disebut bilangan asli (bilangan
positif)
Bilangan -1, -2, -3, -4, … disebut bilangan negatif
Bilangan bulat adalah bilangan yang terdiri bilangan
positif, 0 (nol) dan bilangan negatif.
Bilangan bulat dapat digambarkan pada gambar garis
bilangan berikut :
-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9
Urutan bilangan-bilangan bulat pada garis bilangan makin ke kanan bilangan
itu makin besar (lebih besar “>”) sedangkan makin ke kiri bilangan itu makin
kecil (lebih kecil “<“).

5. BILANGAN BULAT
Contoh :
Pada suatu garis bilangan, bilangan -3 terletak di
sebelah kiri bilangan 2 sehingga ditulis -3< 2 atau
2> -3. Adapun bilangan -3 terletak di sebelah
kanan -5 sehingga ditulis -3 > -5 atau -5 < -3.
Jika kedua kalimat di atas digabungkan maka
diperoleh -5 < -3 < 2 atau 2 > -3 > -5.

6. B. Penjumlahan dan Pengurangan
1. Penjumlahan
Penjumlahan dua bilangan dapat ditunjukan dengan garis
bilangan.
Contoh:
a. 2 + 5 = 7
-5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

7. BILANGAN BULAT
b. 3 + (-4) = -1
-5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
c. (-2)+ (-3) = -5
-5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8

8. Perhatikan Garis Bilangan Berikut
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
Dari gambar di atas menunjukkan bahwa :
-1 lawan (invers) dari 1 -3 lawan (invers) dari 3
-2 lawan (invers) dari 2 -4 lawan (invers) dari 4
Kesimpulan : -a adalah lawan atau invers dari a
-a + a = 0

9. Sifat-Sifat Penjumlahan Bilangan Bulat
Untuk a, b, dan c bilangan bulat maka berlaku sifat-sifat:
a. Tertutup yaitu jumlah dua atau bilangan bulat menghasilkan
bilangan bulat
b. Sifat Pertukaran (Komutatif)
c. Sifat Pengelompokan (assosiatif)
d. Unsur identitas penjumlahan adalah 0
a + b = r
a + b = b + a
(a + b) + c = a + (b + c)
a + 0 = 0 + a = a

10. 2. Pengurangan Bilangan Bulat
i. Pengurangan pada bilangan cacah tidak tertutup
Contoh : a + 2 = 1, a bilangan cacah
Pengganti “a” tidak ada sebab tidak ada sembarang bilangan cacah jika ditambah 2
hasilnya = 1
ii. Pengurangan pada bilangan bulat tertutup
Contoh : 5 – 8 = -3 -3 bilangan bulat
iii. Pengurangan bilangan bulat dengan garis bilangan
Contoh : 2 – 3 = -1
-5 -4 -3 -2 -1 0 1 2 3 4 5
iv. Pengurangan bilangan bulat sama saja dengan menambah dengan
lawan/invers
Contoh : a – b = a + (-b) 3 – 4 = 3 + (-4) = -1

11. C. Perkalian dan Pembagian
1. Perkalian
a. Perkalian didefinisikan sebagai penjumlahan berulang.
Contoh : 2 x 4 = 4 + 4 = 8
b. Sifat-sifat dari perkalian bilangan bulat
Contoh :
1. 4 x 0 = 0 Perkalian 0 dengan bilangan bulat menghasilkan 0
2. 2 x (-4) = -8
-2 x (-1) = 2
-4, -2, -1 dan 2 bilangan bulat jadi tertutup.
3. Berlaku sifat komutatif
Contoh : 2 x 3 = 3 x 2 = 6
a x 0 = 0 x a = 0
a x b = b x a

12. Perkalian Bilangan Bulat
4. Unsur identitas
Perkalian bilangan bulat dengan 1 adalah bilangan bulat itu sendiri.
Contoh : (-6) x 1 = 1 x (-6) = -6
5. Berlaku sifat assosiatif
Contoh : (3 x 4) x 5 = 3 x (4 x 5) = 60
6. Sifat distributif perkalian terhadap penjumlahan
Contoh : 5 x (2 + 4) = 5 x 6 = 30
(a x b) x c = a x (b x c)
a x 1 = 1 x a = a
a x (b + c) = (a x b) + (a x c)

13. 2. Pembagian Bilangan Bulat
Pembagian merupakan kebalikan dari perkalian.
Jika p, q dan r bilangan maka p : q = r sama artinya dengan q x r = p untuk
q ≠ 0.
Sifat-sifat pembagian bilangan bulat
1. 3 : 4 = ( bukan bilangan bulat)
Jadi pembagian bilangan bulat tidak tertutup.
2. 5 : 0 = 0 salah sebab 0 x 0 ≠ 5
Jadi pembagian dengan nol (0) tidak didefinisikan.
3. 0 : 3 = a sama artinya dengan a x 3 = 0
Nilai a yang memenuhi adalah 0
Jadi pembagian 0 dengan bilangan hasilnya 0
Catatan :
+ x + = +
+ x - = -
- x + = -
-x - = +
+ : + = +
+ : - = -
-: + = -
- : - = +

14. D. Taksiran Pada Bilangan Bulat
Untuk mengalikan dua bilangan bulat dapat dilakukan dengan taksiran
hasilnya dengan membulatkan faktor-faktor perkaliannya.
Hasilnya menggunakan lambang “≈” (dibaca mendekati)
Untuk pembulatan aturannya :
- Jika angka satuannya 1 s/d 4 maka angka satuannya dihilangkan.
- Jika angka satuannya 5 s/d 9 maka angka satuannya dibulatkan ke
angka puluhan (ke atas).
Contoh :
1. 57 angka satuannya 7 dibulatkan menjadi 1 puluhan 57 ≈ 60
369 ≈ 400
jadi 57 x 369 ≈ 60 x 40 ≈ 24000

15. E. Pemangkatan dan Akar
Perkalian berulang dapat di tulis dalam bentuk bilangan
berulang.
Contoh :
2 x 2 x 2 = 2³ (dibaca 2 pangkat 3) 2 disebut bilangan
pokok dan 3 disebut pangkat.
Jika a bilangan riil dan n bilangan bulat positif maka :
= a x a x a x … x a
n faktor

16. Sifat-sifat Bilangan dengan Pangkat Bilangan
Positif
1.
Contoh : 53 x 51 = (5 x 5 x 5) x 5 = 53+1 = 54
2.
Contoh : = = 45-2
3.
Contoh : (43 )2 = 43 x 43 = (4 x 4 x 4) x (4 x 4 x 4) = 43+3 = 46
ap x aq = ap+q
= ap-q
(ap )q = ap q

17. 4.
Contoh : (3 x 4)3 = (3 x 4) x (3 x 4) x (3 x 4)
= (3 x 3 x3) x (4 x 4 x 4) = 33 x 43
5.
Contoh : ( )4 = x x x = =
6.
Contoh : 02 = 0 x 0 = 0
7.
Contoh : a3 x a3 = = 1 atau a3-3 = a0
(a x b)n = an x bn
( )n =
0n = 0
a0 = 1 a-n = atau an =

18. F. Akar Kuadrat Bilangan Bulat
Akar kuadrat suatu bilangan merupakan kebalikan (invers) dari operasi kuadrat suatu
bilangan.
Notasi akar kuadrat “√”
Notasi akar pangkat tiga “ “
√4 dibaca “akar kuadrat dari 4 atau akar pangkat dua dari 4”
dibaca “akar pangkat tiga dari 8”
Contoh : 22 = 4 = (4) ½ = 22/2 = 21 = 2
= = (-2) 2/3 = -2
Akar pangkat n dari a (n > 2 dan n bilangan asli) dapat :
i. Bernilai positif, jika “a” positif
ii. Bernilai negatif, jika “a” negatif dan “n” ganjil
iii. Tak bernilai jika “a” negatif dan “n” genap.

19. 1. Menghitung Akar Kuadrat Suatu Bilangan
Contoh :
√144 = atau √144 = 12
= 1 x 1 = -
= +
= 22 x 2 =
=
= 12

20. 2. Menentukan Akar Kuadrat suatu Bilangan
dengan Perkalian
Contoh : Tentukan nilai √19
4 5 Jawab : 19 terletak antara
angka 16 dan 25, sehingga
√19 terletak antara √16 dan
√16 19 – 16 = 3 √19 √25 √25 atau antara 4 dan 5.
√19 = 4 + = 4 = 4,33
25 – 16 = 9
Jadi √n = p +

21. Uji Kompetensi 1
1.
-5 -4 -3 -2 -1 0 1 2 3 4 5
Garis bilangan di atas menunjukan penjumlahan…
2. “x” terletak antara -7 dan 3 dapat ditulis….
3. Perkiraan dari 143 x 195 ≈

22. 4. Selisih dua bilangan bulat adalah 15. Jika
bilangan yang terbesar adalah 7. Tentukan
bilangan yang terkecil !
5. Arti dari (4a)4 adalah….
6. Tentukan nilai “m”
m + 4 = -9
7. Jika p = -2, tentukan nilai :
a) P3
b) (P3)2

23. Jawaban
1. 3 + (-7)
2. -7 < x < 3
3. 143 x 195 ≈ 140 x 200 ≈
28000
4. Misal bilangan terkecil
“a”
7- a = 15
7 + (-7)-a = 15 + (-7)
0 - a = 8
-a = 8
a = -8
5. (4a)4 = 4a x 4a x 4a x 4a
6. m = -9 – 4 = -13
7. a. (-2)3 = -8
b. (23)2 = 26 = 64

24. Daftar Pustaka
Suratmin, S.Pd. 2006. Lks Matematika Sportif untuk
SMP/MTS kelas VII. Solo: CV. Harapan Baru.

25. •Terima Kasih 
Terima Kasih 