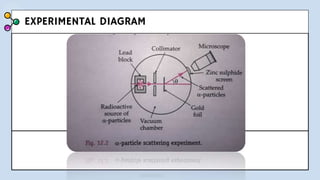
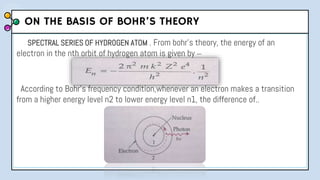
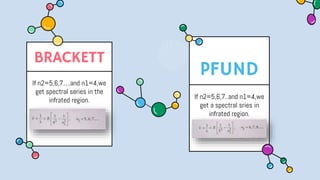
1) The document discusses Thomson's plum pudding model of the atom and its limitations. It then describes Rutherford's alpha scattering experiment, the conclusions he drew, and his nuclear model of the atom. 2) Bohr's model improved upon Rutherford's by proposing quantized electron orbits and energy levels based on Planck's quantum theory. This allowed Bohr to explain the hydrogen spectral series. 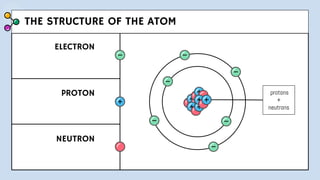3) The document provides details of Thomson, Rutherford, and Bohr's atomic models, including their postulates and limitations. It discusses key experiments and conclusions that improved understanding of atomic structure over time.

1. A T O M S
THE FUNDAMENTAL
12th Grade

2. 01 02
03 04
THOMSON’S MODEL ATOM
Plum pudding model of atom.
SCATTERING EXPERIMENT
Rutherford – alpha particle
BOHAR’S QUANTISATION
Atomic Model , Theory of Hydrogen , Spectra Series
ENERGY LEVEL DIAGRAM
Limitation of Bohr’s theory
TABLE OF CONTENTS

3. WHOA!
KARAN DEEP SINGH
12TH NON MEDICAL

4. 01
THOMSON’S MODEL OF AN ATOM
PLAM PUDDING MODEL OF AN ATOM

5. THOMSON’S MODEL OF AN ATOM
IN 1898 J.J THOMSON PROPOSED THAN AN ATOM IS A SPHERE OF
POSITIVELY CHARGED MATTER WITH ELECTRON EMBENDED IN IT.
Thomson proposed the plum pudding model of the atom, which
had negatively-charged electrons embedded within a positively-
charged "soup." Thomson assumed that an electron is two thousand
times lighter than a proton and believed that an atom is made up of
thousands of electrons. In this atomic structure model, he
considered atoms surrounded by a cloud having positive as well as
negative charges. The demonstration of the ionization of air by X-ray
was also done by him together with Rutherford. They were the first
to demonstrate it. Thomson’s model of an atom is similar to a plum
pudding.

6. POSTULATES OF THOMSON’S ATOMIC MODEL
● Postulate 1: An atom consists of a positively charged sphere with
electrons embedded in it
● Postulate 2: An atom as a whole is electrically neutral because the
negative and positive charges are equal in magnitude
● Postulate 3 : The electron are arranged in such a manner that
mutual repulsion are balanced by their attraction with positively
charged matters. Thus atom as a whole Stable and Nutural .

7. LIMITATION OF THOMSON’S MODEL
● It failed to explain the stability of an atom because his model of atom
failed to explain how a positive charge holds the negatively charged
electrons in an atom. Therefore, This theory also failed to account for
the position of the nucleus in an atom.
● Thomson’s model failed to explain the scattering of alpha particles by
thin metal foils.
● No experimental evidence in its support.

8. 02
RUTHERFORD SCATTERING EX.
Scattering of a-particle
Rutherford Atomic Model – The plum pudding model given
by J. J. Thomson failed to explain certain experimental
results associated with the atomic structure of elements.
Ernest Rutherford, a British scientist conducted an
experiment and based on the observations of this
experiment, he explained the atomic structure of elements
and proposed Rutherford’s Atomic Model

9. RUTHERFORD’S EXPERIMENT ARRANGEMENT
A schematic arrangement of the GeigerMarsden experiment is
shown. A Radioative source of alpha particle like is enclosed in
thick lead block,provided with a narrow opening.The a particles from
this source are collimated into a narrow beam through a narrow slit.
The beam is allowed to fall on a thin gold foil of thickness 2.1*10*-7
m . The a particle scattered in different directions and observed with
the help of rotatable detector which consists of zinc sulphide screen
and microscope. Whenever an alpha particle strikes the screen ,it
produces a tiny flash, or scintillation, which is viewed through the
microscope. In this way, the number of a particle as different angles
can be counted .The whole apparatus in inclosed in an evacuted
chamber to avoid scattering of a particle by air molecules.

10. EXPERIMENTAL DIAGRAM

11. OBSEVATION OF RUTHERFORD’S SCATTERING EXPERIMENT
● The observations made by Rutherford led him to conclude that:
● A major fraction of the α-particles bombarded towards the gold sheet passed
through the sheet without any deflection, and hence most of the space in an atom
is empty.
● Some of the α-particles were deflected by the gold sheet by very small angles, and
hence the positive charge in an atom is not uniformly distributed. The positive
charge in an atom is concentrated in a very small volume.
● Very few of the α-particles were deflected back, that is only a few α-particles had
nearly 180o angle of deflection. So the volume occupied by the positively charged
particles in an atom is very small as compared to the total volume of an atom.

12. Based on the above observations and conclusions, Rutherford proposed the atomic structure of
elements. According to the Rutherford atomic model:
• The positive charge and most of the mass of an atom is concentrated in an extremely small
volume. He called this region of the atom as a nucleus.
• Rutherford’s model proposed that the negatively charged electrons surround the nucleus of
an atom. He also claimed that the electrons surrounding the nucleus revolve around it with
very high speed in circular paths. He named these circular paths as orbits.
• Electrons being negatively charged and nucleus being a densely concentrated mass of
positively charged particles are held together by a strong electrostatic force of attraction.
RUTHERFORD’S ATOMIC MODEL

13. Although the Rutherford atomic model was based on experimental observations, it failed to explain
certain things.
o Rutherford proposed that the electrons revolve around the nucleus in fixed paths called orbits.
According to Maxwell, accelerated charged particles emit electromagnetic radiations and hence
an electron revolving around the nucleus should emit electromagnetic radiation. This radiation
would carry energy from the motion of the electron which would come at the cost of shrinking of
orbits. Ultimately the electrons would collapse in the nucleus. Calculations have shown that as
per the Rutherford model, an electron would collapse into the nucleus in less than 10-8 seconds.
So the Rutherford model was not in accordance with Maxwell’s theory and could not explain the
stability of an atom.
o One of the drawbacks of the Rutherford model was also that he did not say anything about the
arrangement of electrons in an atom which made his theory incomplete.
o Although the early atomic models were inaccurate and failed to explain certain experimental
results, they formed the base for future developments in the world of quantum mechanics.
LIMITATIONS RUTHERFORD’S MODEL

14. An atom consists of a small and massive central core in which the entire positive charge
and almost the whole mass of the atom are concentrated. This core is called the nucleus.
The size of the nucleus (≈ 10-15 m) is very compared to the size of the atom (≈ 10-10
m). small as
The nucleus is surrounded by a suitable number of electrons so that their total negative
charge is equal to the total positive charge on the nucleus and the atom as a whole is
electrically neutral.

15. 03
BOHAR’S QUANTISATION
Hydrogen Spectral series

16. 1. According to Bohr, Every atom Consist of a Central Core Called nucleus, in which entire
the charge and almost entire mass of atom is Concentrated A Suitable no of electrons
revolve around the Nucleus in Circular orbit.
2. According to Bohr , can revolve in certain non radiating orbit called Stationary orbit for
which the total angular momentum of the revolving è is Integral multiple of the an
nh/2π (n=integral) --------1
Angular momentum=mvr -----------2
From 1 and 2---------------------
mvr = nh/2π
The Quantum Condition limits the no. of allowed orbits. The election while
revolving in Such orbits, Shall not lose energy.
BOHR’S QUANTISATION CONDITION

17. The emission or absorption of energy occur only When é Jumps from one
of its orbit to another. Orbit and it can be given as..
E2 – E1 = hV
→→The energy of hydrogen atom in any shell can be given as
E = -13.6ev/n*2
For n=1, E1=-13.6/1*2 = -13.6ev
For n=2 E2=-13.6/2*2 = -13.6/4 = 3.4ev
hv = E2 – E1
hv = -3.4-(-13.6)
hv = -3.4+13.6
hv = 10.2 ev

18. Postulate of Bohr’s theory of hydrogen atom.
o Accepting the Rutherfords nucleus model of an an atom as well as the Plank’s quantum theory , Bohr
proposed an atomic model to explain the spectra emitted by hydrogen atoms. Bohr’s atomic model, so
called Planetory model of the atom,is based on the following Postulates :
1. Nuclear concept. An atom consists of a small and massive central core, called nucleus around
which planetary electrons revolve. The centripetal force required for their rotation is provided by the
electrostatic attraction between the electrons and the nucleus.
2. Quantum condition. Of all the possible circular orbits allowed by the classical theory, the electrons
are permitted to circulate only in those orbits in which the angular momentum of an electron is an
integral multiple of h 2π ;h being Planck's constant. Therefore, for any permitted orbit,
BOHR’S ATOMIC MODEL: POSTULATE

19. L=mvr=nh/2π , (n=1,2,3………)
● where L, m and v are the angular momentum, mass and speed of the electron, r is the radius of
the permitted orbit and n is positive integer called principal quantum number. The above equation
is Bohr's famous quantum condition.
● 3. Stationary orbits. While revolving in the permi- ssible orbits, an electron does not radiate
energy. These non-radiating orbits are called stationary orbits.
● 4. Frequency condition. An atom can emit or absorb radiation in the form of discrete energy
photons only when an electron jumps from a higher to a lower orbit or j lower to a higher orbit,
respectively. If E, and E, are the from a energies associated with these permitted orbits, then the
frequency v of the emitted or absorbed radiation is given by
● hv = E₂-E1
● .:.This is Bohr’s famous frequency condition.

20. Using Bohr's postulates, derive an expression for the radii of the permitted orbits in the hydrogen
atom. Show that the speed of electron in the innermost orbit of H-atom is 1/137 times the
speed of light. Also obtain an expression for the total energy of an electron in the nth orbit of an
atom. What does negative value of this energy signify? What is Bohr's radius?
Bohr's Theory of hydrogen atom: Radii of permitted orbits. According to Bohr's theory, a hydrogen
atom consists of a nucleus with a positive charge Ze, and a single electron of charge -e, which
revolves around it in a circular orbit of radius r. Here Z is the atomic number and for hydrogen
Z=1. The electrostatic force of attraction between the nucleus and the electron is
BOHR’S THEORY OF HYDROGEN ATOM

21. TO KEEP THE ELECTRON IN ITS ORBIT, THE CENTRIPETIAL FORCE ON THE ELECTRON
MUST BE EQUAL TO ELECTROSTATIC ATTRACTION . THEREFORE,
Where m is the mass of electron and v,its speed in an orbit of radius r .

22. BOHR’S QUANTISATION CONDITION FOR ANGULAR
MOMENTUM

23. —emission of a spectral lines
“Spectral Series of Hydrogen Atom.”

24. SPECTRAL SERIES OF HYDROGEN ATOM . From bohr’s theory, the energy of an
electron in the nth orbit of hydrogen atom is given by –
According to Bohr’s frequency condition,whenever an electron makes a transition
from a higher energy level n2 to lower energy level n1, the difference of..
ON THE BASIS OF BOHR’S THEORY

25. ●Energy appears in the form of a photon .The frequency v of the emitted photon is
given by –
As c=v/I ,therfore wave number v, which is the reciprocal of wavelenght/I, is given
by-

26. The above equation is RYDBERG FORMULA for the spectrum of Hydroden atom.This
formula indicates that the radiation emitted hdrogen atom consists of certain
specific wavelenght or frequecies , the value of which depends on qutum number n1
and n2.
WAVE NUMBER CAN BE ALSO

27. SPECTRAL SERIES OF HYDROGEN ATOM

28. LYMAN
Electron jumps from energy
level n2=2,3,4…. To lower
n=1. belonging to
Ultravoilet region.
Balmer
Spectral Series
corresponding to the
transition n2=3,4,5… to
n=2 belongs to visible .
Region.
Paschen
If n2=4,5,6….and n1=3,
we get a spectral series in
infrared region.

29. BRACKETT
If n2=5,6,7…and n1=4,we
get spectral series in the
infrated region.
PFUND
If n2=5,6,7..and n1=4,we
get a spectral sries in
infrated region.

30. THANKQ

31. THE STRUCTURE OF THE ATOM
ELECTRON
PROTON
NEUTRON
protons
+
neutrons