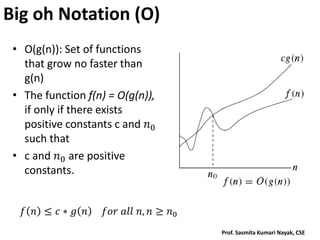
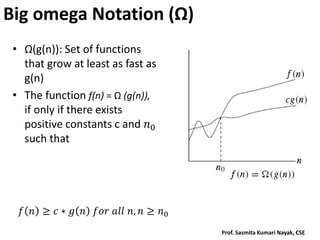
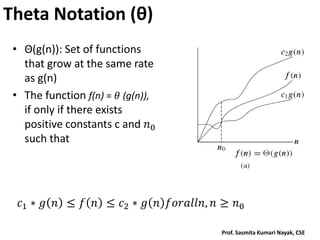
The document discusses algorithm analysis and asymptotic notation. It introduces orders of growth, best-case, worst-case and average-case efficiencies. The key asymptotic notations of big-O, big-Omega and big-Theta are defined and examples are provided to illustrate how to determine the asymptotic notation of algorithms. The analysis of both recursive and non-recursive algorithms is covered, along with examples such as sequential search and finding the maximum element in an array.

1. MATHEMATICAL PROBLEM
SOLVING
By
Prof. Sasmita Kumari Nayak
Dept. of CSE
Orders of Growth
Prof. Sasmita Kumari Nayak, CSE

2. Introduction
• Orders of Growth
• Best-Case, Worst-Case and Average-Case Efficiencies,
• Asymptotic Notations
• Analysis of Recursive Algorithms
• Analysis of Non-Recursive Algorithms
Prof. Sasmita Kumari Nayak, CSE

3. Orders of Growth
• An order of growth is a set of functions whose
asymptotic growth behavior is considered equivalent.
• consider only the leading term of a formula and ignore
the constant coefficient.
• Example:
– How much faster will algorithm run on computer that
is twice as fast?
– How much longer does it take to solve problem of
double input size?
Prof. Sasmita Kumari Nayak, CSE

4. Cont…
Prof. Sasmita Kumari Nayak, CSE

5. Best-Case, Worst-Case and Average-Case
• Algorithm efficiency depends on the input size n.
– Worst case: Cworst(n) – maximum number of times
the basic operation is executed over inputs of size n
– Best case: Cbest(n) – minimum # times over inputs of
size n
– Average case: Cavg(n) – “average” over inputs of size n
Prof. Sasmita Kumari Nayak, CSE

6. Cont…
• For some algorithms efficiency depends on type of input.
– Example: Sequential Search
• Problem: Given a list of n elements and a search key K, find an element equal
to K, if any.
• Algorithm: Scan the list and compare its successive elements with K until
either a matching element is found (successful search) or the list is exhausted
(unsuccessful search)
• Given a sequential search problem of an input size of n, what kind of
input would make the running time the longest?
• How many key comparisons?
Prof. Sasmita Kumari Nayak, CSE

7. Ex: Sequential Search Algorithm
ALGORITHM SequentialSearch(A[0..n-1], K)
//Searches for a given value in a given array by sequential search
//Input: An array A[0..n-1] and a search key K
//Output: Returns the index of the first element of A that matches K or –1
if there are no matching elements
i 0
while i < n and A*i+ ≠ K do
i  i + 1
if i < n //A[I] = K
return i
else
return -1
Worst-Case: Cworst(n) = n
Best-Case: Cbest(n) = 1
Prof. Sasmita Kumari Nayak, CSE

8. Asymptotic Notations
• It describe the algorithm efficiency and performance for
large instance characteristics (e.g. numbers, size of the
array etc.).
• 3 notations used to compare orders of growth of an
algorithm’s basic operation count
– big oh (O), big theta (), omega ()
• asymptotic functions :
Prof. Sasmita Kumari Nayak, CSE
Constant function: 1, 2, 3 … Exponential:2𝑛
, …
Logarithmic: log n . . . Factorial:𝑛!, …
Linear: n, 2n … Cubic:𝑛3, …
Quadratic: 𝑛2, …

9. Big oh Notation (O)
• O(g(n)): Set of functions
that grow no faster than
g(n)
• The function f(n) = O(g(n)),
if only if there exists
positive constants c and 𝑛0
such that
• c and 𝑛0 are positive
constants.
Prof. Sasmita Kumari Nayak, CSE
𝑓 𝑛 ≤ 𝑐 ∗ 𝑔 𝑛 𝑓𝑜𝑟 𝑎𝑙𝑙 𝑛, 𝑛 ≥ 𝑛0

10. Big omega Notation (Ω)
• Ω(g(n)): Set of functions
that grow at least as fast as
g(n)
• The function f(n) = Ω (g(n)),
if only if there exists
positive constants c and 𝑛0
such that
Prof. Sasmita Kumari Nayak, CSE
𝑓 𝑛 ≥ 𝑐 ∗ 𝑔 𝑛 𝑓𝑜𝑟 𝑎𝑙𝑙 𝑛, 𝑛 ≥ 𝑛0

11. Theta Notation (θ)
• Θ(g(n)): Set of functions
that grow at the same rate
as g(n)
• The function f(n) = 𝜃 (g(n)),
if only if there exists
positive constants c and 𝑛0
such that
Prof. Sasmita Kumari Nayak, CSE
𝑐1 ∗ 𝑔 𝑛 ≤ 𝑓 𝑛 ≤ 𝑐2 ∗ 𝑔 𝑛 𝑓𝑜𝑟𝑎𝑙𝑙𝑛, 𝑛 ≥ 𝑛0

12. Numerical problems
Example 1: Suppose given constant functions:𝑓 𝑛 = 16,
𝑓 𝑛 = 27, 𝑓 𝑛 = 9.
Solution: Then for satisfying the O notation condition, the
above expression can be expressed as follows:
𝑓 𝑛 ≤ 16 ∗ 1𝑤𝑕𝑒𝑟𝑒 𝑐 = 16, 𝑛0 = 0 𝑎𝑛𝑑𝑔 𝑛 = 1
𝑓 𝑛 ≤ 27 ∗ 1𝑤𝑕𝑒𝑟𝑒 𝑐 = 27, 𝑛0 = 0 𝑎𝑛𝑑 𝑔 𝑛 = 1
𝑓 𝑛 ≤ 9 ∗ 1𝑤𝑕𝑒𝑟𝑒 𝑐 = 9, 𝑛0 = 0 𝑎𝑛𝑑 𝑔 𝑛 = 1
Thus, for above function we can specify the 𝑂 notation as
𝑂 1 . So, 𝑓 𝑛 = 𝑂 1 .
Prof. Sasmita Kumari Nayak, CSE

13. Numerical problems
Example 2: Find out the 𝑂 notation for the given linear
function 𝑛 = 3𝑛 + 5 .
Solution: For 𝑓 𝑛 = 3𝑛 + 5, when ‘n’ is at least 5, 𝑛 ≥ 5
3𝑛 + 5 ≤ 3𝑛 + 𝑛
≤ 4𝑛
So, 𝑓 𝑛 = 𝑂 𝑛 𝑤𝑕𝑒𝑟𝑒 𝑐 = 4 𝑎𝑛𝑑 𝑔 𝑛 = 𝑛
Thus, the above function is bounded by a linear function.
We can also prove the above function in another way as:
3𝑛 + 5 ≤ 3𝑛 + 5𝑛 = 8𝑛, 𝑓𝑜𝑟 𝑛 ≥ 1, 𝑤𝑕𝑒𝑟𝑒 𝑐 =
8 𝑎𝑛𝑑 𝑛0 = 1, which satisfies the O notation.
Prof. Sasmita Kumari Nayak, CSE

14. Numerical problems
Example 3: Find out the 𝑂 notation for the given quadratic
function 𝑛 = 10𝑛2 + 7 .
Solution: 10𝑛2 + 7 ≤ 11𝑛2, 𝑤𝑕𝑒𝑟𝑒 𝑐 = 11,
𝑔 𝑛 = 𝑛2𝑎𝑛𝑑 𝑛0 = 3 So, 𝑓 𝑛 = 𝑂 𝑛2
Prof. Sasmita Kumari Nayak, CSE

15. Numerical problems
Example 4: Suppose given constant functions: 𝑓 𝑛 = 16,
𝑓 𝑛 = 27, 𝑓 𝑛 = 9.
Solution: Then for satisfying the Ω notation condition, the
above expression can be expressed as follows:
𝑓 𝑛 ≥ 16 ∗ 1𝑤𝑕𝑒𝑟𝑒𝑐 = 16, 𝑛0 = 0 ∧ 𝑔 𝑛 = 1
𝑓 𝑛 ≥ 27 ∗ 1𝑤𝑕𝑒𝑟𝑒𝑐 = 27, 𝑛0 = 0 ∧ 𝑔 𝑛 = 1
𝑓 𝑛 ≥ 9 ∗ 1𝑤𝑕𝑒𝑟𝑒𝑐 = 9, 𝑛0 = 0 ∧ 𝑔 𝑛 = 1
Thus, for above function we can specify the Ω notation as
Ω 1 . So, 𝑓 𝑛 = Ω 1 .
Prof. Sasmita Kumari Nayak, CSE

16. Numerical problems
Example 5: Find out the Ω notation for the given linear
function 𝑛 = 3𝑛 + 5 .
Solution: Let 3𝑛 ≤ 3𝑛 + 5
3𝑛 + 5 ≥ 3𝑛 𝑤𝑕𝑒𝑟𝑒𝑐 = 3, 𝑛0 = 1
So, 𝑓 𝑛 = Ω 𝑛 𝑤𝑕𝑒𝑟𝑒𝑔 𝑛 = 𝑛 ∧ 𝑛 ≥ 1
Prof. Sasmita Kumari Nayak, CSE

17. Numerical problems
Example 6: Find out the Ω notation for the given quadratic
function 𝑛 = 27𝑛2 + 16𝑛 .
Solution: Consider the function 𝑓 𝑛 = 27𝑛2 + 16𝑛 for
27𝑛2
+ 16𝑛 ≥ 27𝑛2
where 𝑐 = 27, 𝑛0 = 1
So, 𝑓 𝑛 = Ω 𝑛 𝑤𝑕𝑒𝑟𝑒𝑔 𝑛 = 𝑛2
∧ 𝑛 ≥ 1
Prof. Sasmita Kumari Nayak, CSE

18. Numerical problems
Example 7: Suppose given constant functions: 𝑓 𝑛 = 16.
Find out the theta notation of given constant function.
Solution: Consider the function𝑓 𝑛 = 16. Then for
satisfying the big theta notation, the given function can be
written as: 15 ∗ 1 ≤ 𝑓 𝑛 ≤ 16 ∗ 1𝑤𝑕𝑒𝑟𝑒𝑐1 = 15, 𝑐2 =
16, 𝑔 𝑛 = 1 ∧ 𝑛0 = 0. So, 𝑓 𝑛 = 𝜃 1
Prof. Sasmita Kumari Nayak, CSE

19. Numerical problems
Example 8: Find out the 𝜃 notation for the given linear
function 𝑛 = 3𝑛 + 5 .
Solution: Let 3𝑛 < 3𝑛 + 5𝑓𝑜𝑟𝑎𝑙𝑙𝑛, 𝑐1 = 3
Also 3𝑛 + 5 ≤ 4𝑛𝑓𝑜𝑟𝑛 ≥ 5, 𝑐2 = 4, 𝑛0 = 5
3𝑛 < 3𝑛 + 5 ≤ 4𝑛 𝑤𝑕𝑒𝑟𝑒𝑐1 = 3, 𝑐2 =
4, 𝑛0 = 5 ∧ 𝑔 𝑛 = 𝑛
So, 𝑓 𝑛 = 𝜃 𝑛
Prof. Sasmita Kumari Nayak, CSE

20. Numerical problems
Example 9: Find out the 𝜃 notation for the given
exponential function 𝑓 𝑛 = 4 ∗ 2𝑛 + 3𝑛.
Solution: The above equation can be expressed as:
4 ∗ 2𝑛 < 4 ∗ 2𝑛 + 3𝑛 for all 𝑛 ≥ 𝑛0 = 1, 𝑐1 = 4
Also 𝑛 ≤ 2𝑛
3𝑛 ≤ 3 ∗ 2𝑛
4 ∗ 2𝑛 + 3𝑛 ≤ 7 ∗ 2𝑛𝑓𝑜𝑟𝑎𝑙𝑙𝑛 ≥ 𝑛0 = 1, 𝑐2 = 7
Thus,
4 ∗ 2𝑛 < 4 ∗ 2𝑛 + 3𝑛 ≤ 7 ∗ 2𝑛𝑓𝑜𝑟𝑎𝑙𝑙𝑛 ≥ 𝑛0 = 1, 𝑐1
= 4, 𝑐2 = 7 ∧ 𝑔 𝑛 = 2𝑛
So, 𝑓 𝑛 = 𝜃 2𝑛
Prof. Sasmita Kumari Nayak, CSE

21. Analysis of Non-Recursive Algorithms

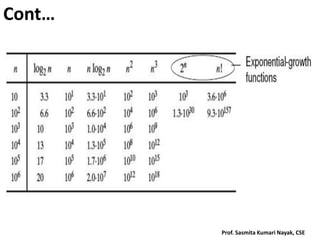
22. Cont…
Example: Maximum Element
Algorithm MaxElement( A[0...n-1] )
maxval ← A[0]
for i ← 1 to n-1 do
if A[i] > maxval then maxval ← A[i]
return maxval
• What is the problem size? n
• Most frequent operation? Comparison in the for loop
• Depends on worst case or best case? No, has to go through
the entire array
• C(n) = number of comparisons
• C(n) = ∑i=1
n-1 1 = n-1 ε Θ(n)