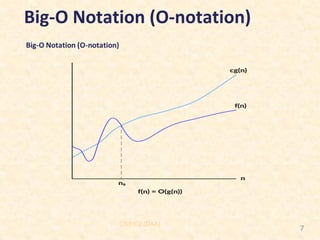
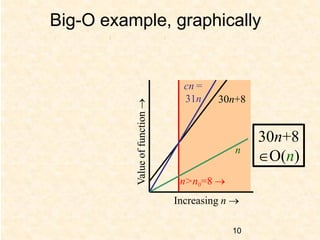
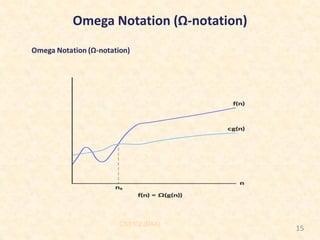
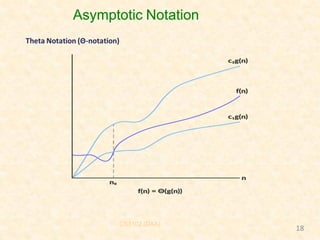
The document outlines the course 'Design and Analysis of Algorithms (CS 3102)' focused on asymptotic notation for analyzing algorithms, detailing the definitions and implications of big-O, omega, and theta notations. It explains how these notations describe algorithmic running times in relation to input size, providing examples to illustrate each type of notation. The course is taught by Dr. Ajit Noonia and is scheduled for the 2024-2025 academic year.

1. Course Name: Design and Analysis of Algorithm
Topic: Asymptotic Notation- Analysis of Algorithms
Course code : CS 3102
Credits : 4
Mode of delivery : Hybrid (Power point presentation)
Faculty : Dr. Ajit Noonia
Email-id : ajit.noonia@jaipur.manipal.edu
B.TECH V SEM CSE
ACADEMIC YEAR: 2024-2025
1

2. Asymptotic Notation- Analysis of Algorithms
CS3102 (DAA) 2

3. Asymptotic Notation
• By now you should have an intuitive feel for asymptotic (big-O)
notation:
• What does O(n) running time mean?
• O(n2)?
• O(n lg n)?
• Our first task is to define this notation more formally and
completely
CS3102 (DAA)
3

4. Asymptotic Notation
Asymptotic notations describe algorithm running time as the
input approaches a specific value.
For instance, in bubble sort, when the input is already sorted,
the algorithm's running time is linear (best case). However,
when the input is in reverse order, the algorithm takes
maximum time (quadratic) to sort the elements (worst case).
The notations used include Theta, Omega, and Big-O.
CS3102 (DAA)
4

5. Big-O Notation (O-notation)
CS3102 (DAA)
5
Definition: Let g and f be functions from the set of natural
numbers to itself. The function f is said to be O(g) (read
big-oh of g), if there is a constant c > 0 and a natural
number n0 such that f(n) ≤ cg(n) for all n ≥ n0 .

6. O- big-oh notation
1<log n < √n < n < n*log n < n2 < n3 < - - - - - - -< 2n < 3n < ----<nn
The Big-O Asymptotic Notation gives us the Upper Bound Idea,
mathematically described below:
f(n) = O(g(n)) if there exists a positive integer n0 and a positive constant c,
such that f(n) ≤ cg(n) ∀ n≥n0
Example
f(n) = 2n + 3

7. CS3102 (DAA)
7
Big-O Notation (O-notation)

8. The Gist of Big-Oh
Take functions f(n) & g(n), consider only the most
significant term, and remove constant multipliers:
▪ 5n+3 → n
▪ 7n+.5n2+2000 → n2
▪ 300n+12+nlogn → n log n
Then compare the functions; if f(n) ≤ g(n), then f(n) is
in O(g(n))
CS3102 (DAA) 8

9. More Examples
9
• Show that 30n+8 is O(n).
– Show c,n0
: 30n+8  cn, n>n0 .
• Let c=31, n0=8.Assume n>n0=8.Then
cn = 31n = 30n + n > 30n+8, so 30n+8 < cn.

10. n>n0=8 →
Increasing n →
Big-O example, graphically
Value
of
function
→
n
30n+8
cn =
31n
10
30n+8
O(n)

11. There is no unique set of values for n0 and c in proving the
asymptotic bounds.
Prove that 100n + 5 = O(n2)
– 100n + 5 ≤ 100n + n = 101n ≤ 101n2
for all n ≥ 5
n0= 5 and c = 101 is a solution
– 100n + 5 ≤ 100n + 5n = 105n ≤ 105n2
for all n ≥ 1
n0= 1 and c = 105 is also a solution
Must find SOME constants c and n0that satisfy the asymptotic notation relation
No Uniqueness
•
•

12. Big Oh: Common Categories
From fastest to slowest
O(1) constant (or O(k) for constant k)
O(log n) logarithmic
O(n) linear
O(n log n) "n log n”
O(n2) quadratic
O(n3) cubic
O(nk) polynomial (where is k is constant)
O(kn) exponential (where constant k > 1)
CS3102 (DAA) 12

13. Omega Notation (Ω-notation)
CS3102 (DAA)
13
Definition: Let g and f be functions from the set of natural
numbers to itself. The function f is said to be Ω(g) (read
Omega Notation of g), if there is a constant c > 0 and a
natural number n0 such that f(n) ≥ cg(n) for all n ≥ n0.

14. O- big-oh notation
1<log n < √n < n < n*log n < n2 < n3 < - - - - - - -< 2n < 3n < ----<nn
The Omega Notation (Ω-notation) Notation gives us the Lower Bound
Idea, mathematically described below:
f(n) = Ω(g(n)) if there exists a positive integer n0 and a positive constant c,
such that f(n) ≥ cg(n) ∀ n ≥ n0
Example
f(n) = 2n + 3
f(n) = 5n2 + 10

15. Omega Notation (Ω-notation)
CS3102 (DAA)
15

16. Theta Notation (Θ-notation)
Definition: Let g and f be functions from the set of natural numbers to itself. The
function f is said to be Θ(g) (Theta Notation of g) if there exists constant c1 and
c2 > 0 and a natural number n0 such that c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0.
CS3102 (DAA)
16

17. Theta Notation (Θ-notation)
1<log n < √n < n < n*log n < n2 < n3 < - - - - - - -< 2n < 3n < ----<nn
The Theta Notation (Θ-notation) gives us the Tight Bound Idea,
mathematically described below:
f(n) = Θ(g(n)) if there exists a positive integer n0 and a positive constant c1
and c2, such that c1g(n) ≤ f(n) ≤ c2g(n) ∀ n ≥ n0
Example
f(n) = 2n + 3
f(n) = 5n2 + 10

18. Asymptotic Notation
CS3102 (DAA)
18

19. CS3102 (DAA)
19
Example
f(n) = 2 n2 + 3n + 4
f(n) = n2 log(n) + n
f(n) = n!